代码随想录算法训练营四十五天|图论part03

岛屿问题（四）孤岛的总面积

题目描述

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。

现在你需要计算所有孤岛的总面积，岛屿面积的计算方式为组成岛屿的陆地的总数。

输入描述

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0。

输出描述

输出一个整数，表示所有孤岛的总面积，如果不存在孤岛，则输出0。

输入示例

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出示例

1

提示信息

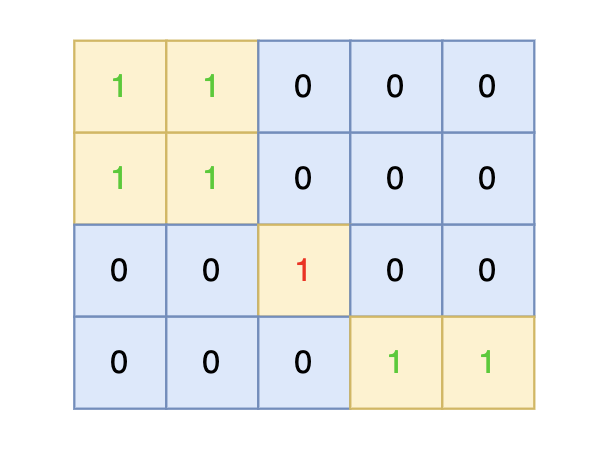
在矩阵中心部分的岛屿，因为没有任何一个单元格接触到矩阵边缘，所以该岛屿属于孤岛，总面积为 1。

数据范围：

1 <= M, N <= 50。

思路：

把矩阵中所有不是孤岛的坐标都由1变为0，最后统计矩阵中1的个数就是孤岛的面积。

深搜法：

import java.util.*;public class Main{private static int ans=0;public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){graph[i][j]=in.nextInt();}}for(int i=0;i<n;i++){if(graph[i][0]==1)dfs(graph,i,0);if(graph[i][m-1]==1)dfs(graph,i,m-1);}for(int j=0;j<m;j++){if(graph[0][j]==1)dfs(graph,0,j);if(graph[n-1][j]==1)dfs(graph,n-1,j);}for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(graph[i][j]==1)ans++;}}System.out.println(ans);}private static int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};public static void dfs(int[][] graph,int x,int y){graph[x][y]=0;for(int i=0;i<4;i++){int nextx=x+dir[i][0];int nexty=y+dir[i][1];if(nextx<0||nexty<0||nextx>=graph.length||nexty>=graph[0].length)continue;if(graph[nextx][nexty]==1){graph[nextx][nexty]=0;dfs(graph,nextx,nexty);}}}
}

广搜法：

import java.util.*;public class Main{private static int ans=0;public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){graph[i][j]=in.nextInt();}}for(int i=0;i<n;i++){if(graph[i][0]==1)bfs(graph,i,0);if(graph[i][m-1]==1)bfs(graph,i,m-1);}for(int j=0;j<m;j++){if(graph[0][j]==1)bfs(graph,0,j);if(graph[n-1][j]==1)bfs(graph,n-1,j);}for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(graph[i][j]==1)ans++;}}System.out.println(ans);}private static int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};public static void bfs(int[][] graph,int x,int y){Queue<int[]> q=new LinkedList<>();q.offer(new int[]{x,y});graph[x][y]=0;while(!q.isEmpty()){int[] cur=q.poll();int curx=cur[0];int cury=cur[1];for(int i=0;i<4;i++){int nextx=curx+dir[i][0];int nexty=cury+dir[i][1];if(nextx<0||nexty<0||nextx>=graph.length||nexty>=graph[0].length)continue;if(graph[nextx][nexty]==1){graph[nextx][nexty]=0;q.offer(new int[]{nextx,nexty});}}}}
}

岛屿问题（五）沉没孤岛

题目描述：

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。

现在你需要将所有孤岛“沉没”，即将孤岛中的所有陆地单元格（1）转变为水域单元格（0）。

输入描述：

第一行包含两个整数 N, M，表示矩阵的行数和列数。

之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述

输出将孤岛“沉没”之后的岛屿矩阵。

输入示例

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出示例

1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1

提示信息

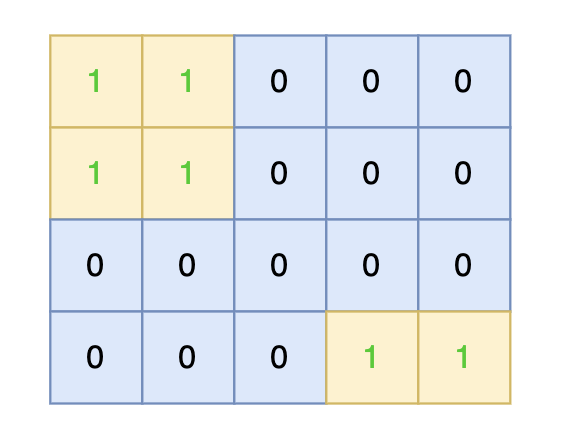
将孤岛沉没：

数据范围：

1 <= M, N <= 50。

思路：

创建一个二维数组res保留不是孤岛的岛屿，也就是发现有靠边的岛屿，就将res对应的单元格置为1，最后输出res即可。

深搜法：

import java.util.*;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){graph[i][j]=in.nextInt();}}int[][] res=new int[n][m];for(int i=0;i<n;i++){if(graph[i][0]==1)dfs(graph,res,i,0);if(graph[i][m-1]==1)dfs(graph,res,i,m-1);}for(int j=0;j<m;j++){if(graph[0][j]==1)dfs(graph,res,0,j);if(graph[n-1][j]==1)dfs(graph,res,n-1,j);}for(int i=0;i<n;i++){for(int j=0;j<m;j++){System.out.print(res[i][j]+" ");}System.out.println();}}private static int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};public static void dfs(int[][] graph,int[][] res,int x,int y){res[x][y]=1;for(int i=0;i<4;i++){int nextx=x+dir[i][0];int nexty=y+dir[i][1];if(nextx<0||nexty<0||nextx>=graph.length||nexty>=graph[0].length)continue;if(graph[nextx][nexty]==1){graph[nextx][nexty]=0;dfs(graph,res,nextx,nexty);}}}
}

广搜法：

import java.util.*;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){graph[i][j]=in.nextInt();}}int[][] res=new int[n][m];for(int i=0;i<n;i++){if(graph[i][0]==1)bfs(graph,res,i,0);if(graph[i][m-1]==1)bfs(graph,res,i,m-1);}for(int j=0;j<m;j++){if(graph[0][j]==1)bfs(graph,res,0,j);if(graph[n-1][j]==1)bfs(graph,res,n-1,j);}for(int i=0;i<n;i++){for(int j=0;j<m;j++){System.out.print(res[i][j]+" ");}System.out.println();}}private static int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};public static void bfs(int[][] graph,int[][] res,int x,int y){Queue<int[]> q=new LinkedList<>();q.offer(new int[]{x,y});res[x][y]=1;while(!q.isEmpty()){int[] cur=q.poll();int curx=cur[0];int cury=cur[1];for(int i=0;i<4;i++){int nextx=curx+dir[i][0];int nexty=cury+dir[i][1];if(nextx<0||nexty<0||nextx>=graph.length||nexty>=graph[0].length)continue;if(graph[nextx][nexty]==1){graph[nextx][nexty]=0;res[nextx][nexty]=1;q.offer(new int[]{nextx,nexty});}}}}
}

岛屿问题（六）水流问题

题目描述：

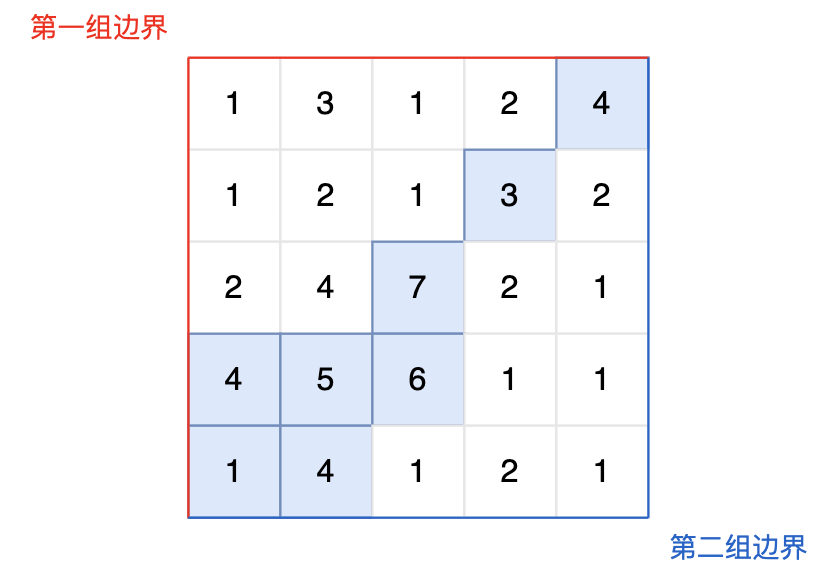
现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。

矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。

输入描述：

第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。

后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。

输出描述：

输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。

输入示例：

5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1

输出示例：

0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1

提示信息：

图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。 

数据范围：

1 <= M, N <= 100。

思路：

分别从第一组边界和第二组边界的节点逆流而上，将遍历过的节点分别用visited1、visited2标记好。

注意这里是“逆流”而上，也就是只有当前节点高度小于下一节点高度才能“逆流”而上，如果大于的话就不算是“逆流”了。

那么这样的话，双方都标记过的节点就是最终结果。

举个例子，从第一组边界边上节点出发：（这里并没有把所有遍历的方向都画出来）

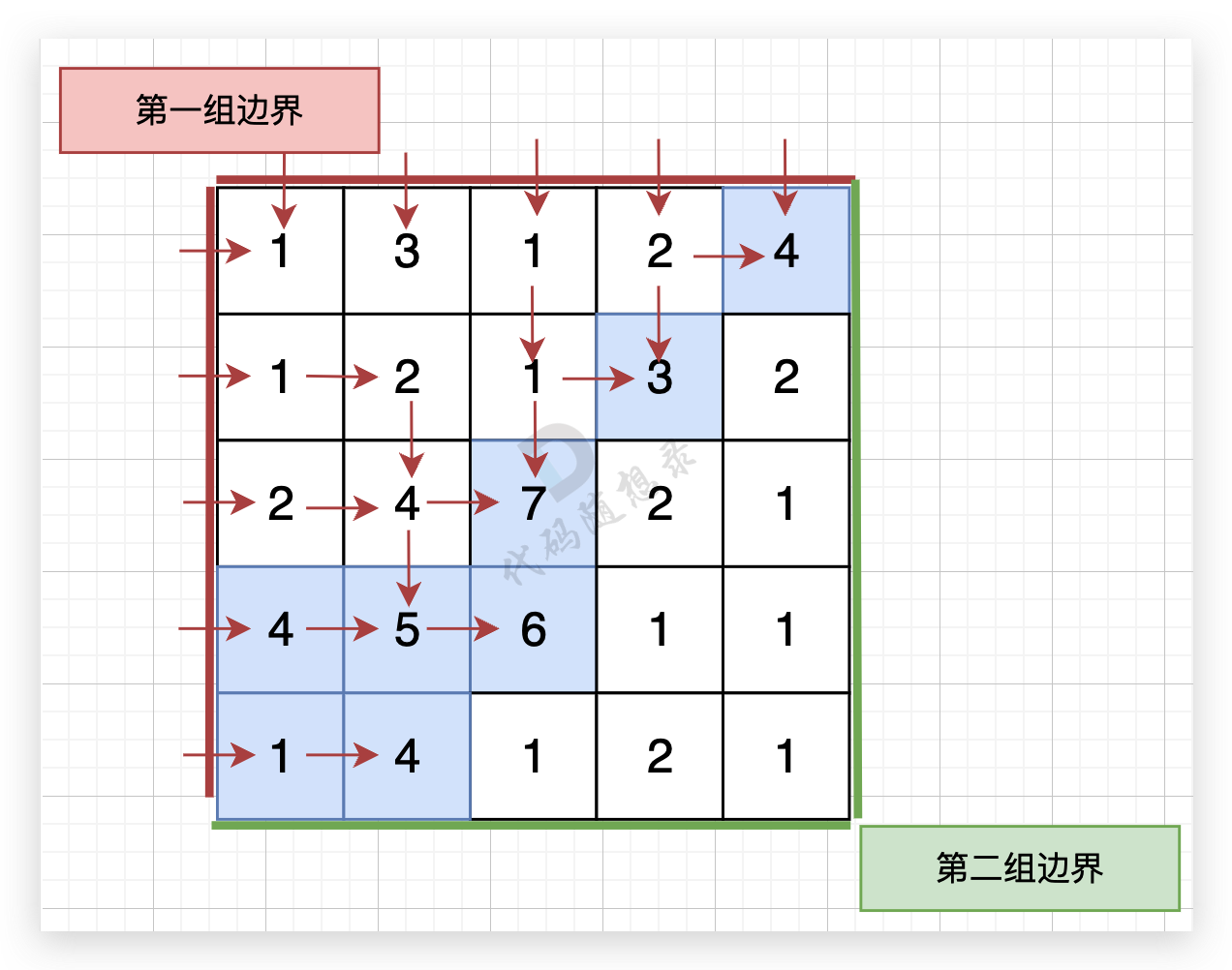
从第二组边界上节点出发，如图：

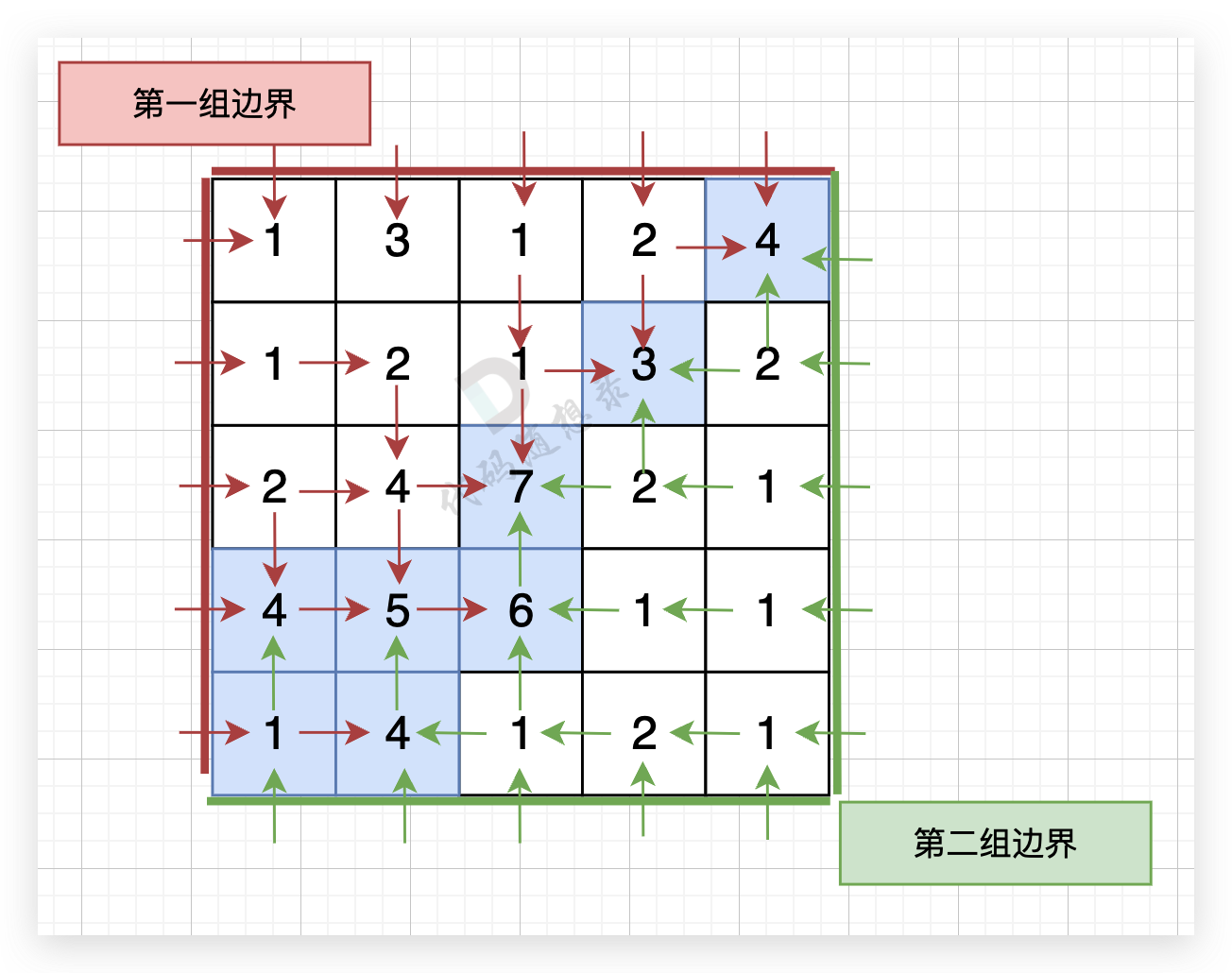
代码如下：（这里只写了深搜的，广搜的套模板写就行了）

import java.util.*;public class Main{public static void main(String[] args){Scanner in=new Scanner(System.in);int n=in.nextInt();int m=in.nextInt();int[][] graph=new int[n][m];for(int i=0;i<n;i++){for(int j=0;j<m;j++){graph[i][j]=in.nextInt();}}boolean[][] visited1=new boolean[n][m];boolean[][] visited2=new boolean[n][m];for(int i=0;i<n;i++){dfs(graph,visited1,i,0);dfs(graph,visited2,i,m-1);}for(int j=0;j<m;j++){dfs(graph,visited1,0,j);dfs(graph,visited2,n-1,j);}for(int i=0;i<n;i++){for(int j=0;j<m;j++){if(visited1[i][j]&&visited2[i][j]){System.out.println(i+" "+j);}}}}private static int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};public static void dfs(int[][] graph,boolean[][] visited,int x,int y){visited[x][y]=true;for(int i=0;i<4;i++){int nextx=x+dir[i][0];int nexty=y+dir[i][1];if(nextx<0||nexty<0||nextx>=graph.length||nexty>=graph[0].length)continue;if(graph[x][y]>graph[nextx][nexty])continue;if(visited[nextx][nexty]==false){dfs(graph,visited,nextx,nexty);}}}
}

岛屿问题（七）建造最大岛屿

题目描述：

给定一个由 1（陆地）和 0（水）组成的矩阵，你最多可以将矩阵中的一格水变为一块陆地，在执行了此操作之后，矩阵中最大的岛屿面积是多少。

岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。

输入描述：

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述：

输出一个整数，表示最大的岛屿面积。

输入示例：

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出示例：

6

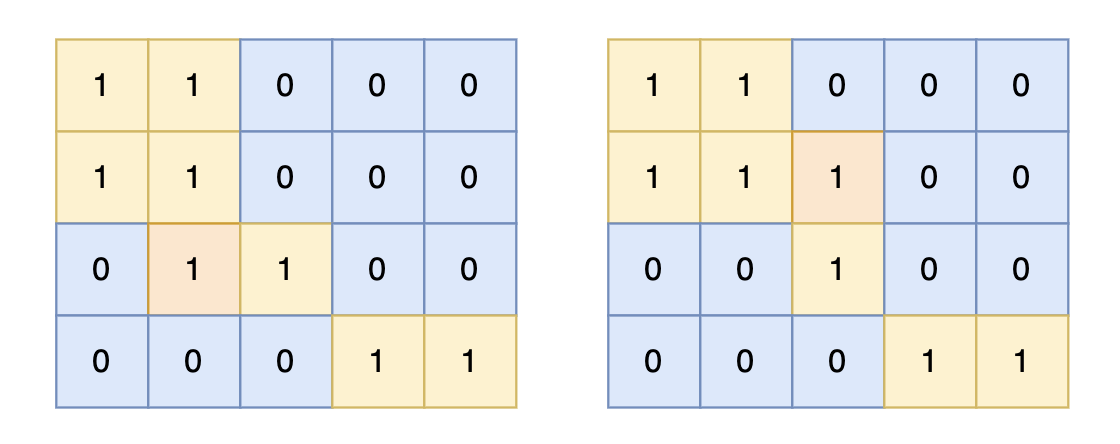
提示信息：

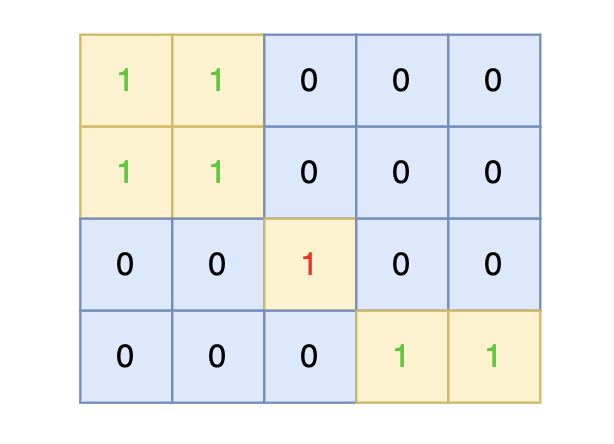
对于上面的案例，有两个位置可将 0 变成 1，使得岛屿的面积最大，即 6。

数据范围：

1 <= M, N <= 50。

思路：

1.首先遍历一次地图，得出各个岛屿的面积，并用map记录，key为岛屿编号，value为岛屿面积。

拿如下的地图来举例：

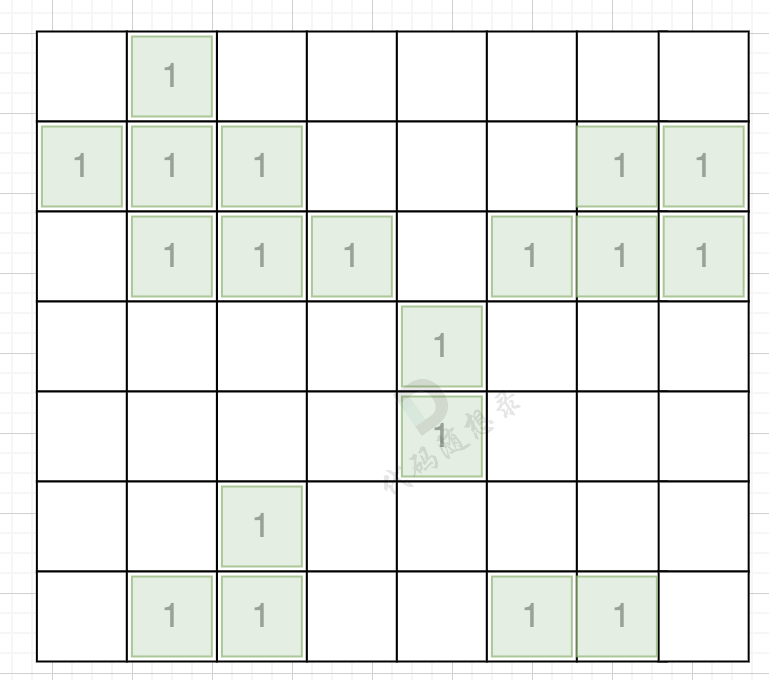
统计岛屿的编号和面积：

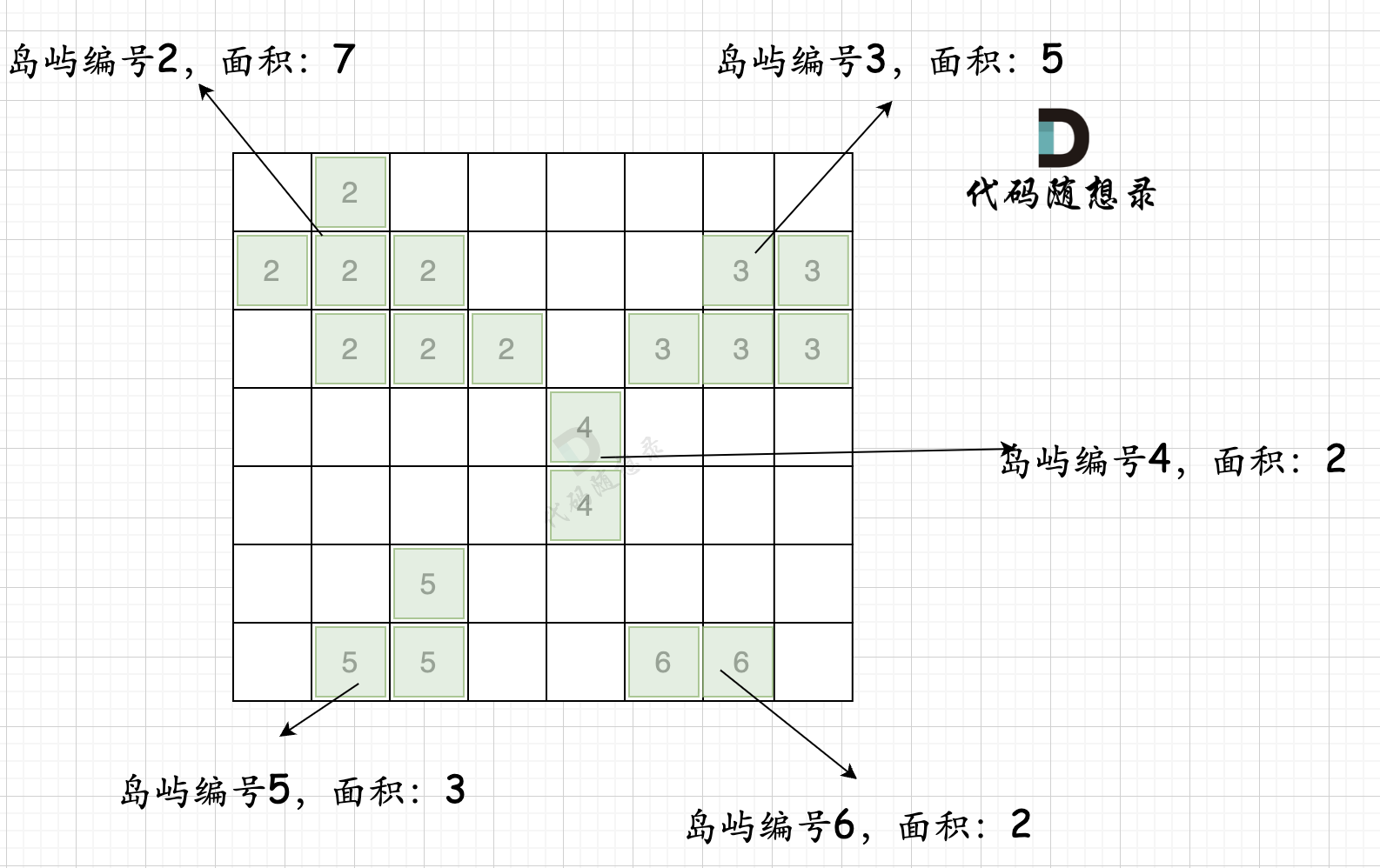
岛屿编号从2开始是因为0、1分别表示海水和陆地，为了区分。

2.再遍历一次地图，找到编号为0的方格，统计该方格周边的岛屿面积并加在一起。遍历完所有编号为0的方格就可以选出一个最大的面积。

代码如下：

import java.util.*;public class Main {static Map<Integer, Integer> map = new HashMap<>();private static int count = 2;private static int ans = 0;private static int res = 0;private static int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};public static void main(String[] args) {Scanner in = new Scanner(System.in);int n = in.nextInt();int m = in.nextInt();int[][] graph = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = in.nextInt();}}boolean isAlland = true;boolean[][] visited = new boolean[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (graph[i][j] == 0) isAlland = false;if (visited[i][j] == false && graph[i][j] == 1) {ans = 1;dfs(graph, visited, i, j);map.put(count, ans);count++;}}}if (isAlland == true) {System.out.println(n * m);return;}Set<Integer> set = new HashSet<>(); //标记访问过的岛屿for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (graph[i][j] == 0) {set.clear();int area = 1;for (int k = 0; k < 4; k++) {int x = i + dir[k][0];int y = j + dir[k][1];if (x < 0 || y < 0 || x >= n || y >= m) continue;if (set.contains(graph[x][y])) continue;if (!set.contains(graph[x][y]) && graph[x][y] > 1) {set.add(graph[x][y]);area += map.get(graph[x][y]);}}res = Math.max(res, area);}}}System.out.println(res);}public static void dfs(int[][] graph, boolean[][] visited, int x, int y) {visited[x][y] = true;graph[x][y] = count;for (int i = 0; i < 4; i++) {int nextx = x + dir[i][0];int nexty = y + dir[i][1];if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length)continue;if (graph[nextx][nexty] == 1 && visited[nextx][nexty] == false) {ans++;dfs(graph, visited, nextx, nexty);}}}
}

在这个地图中，每个节点我们只遍历了一次，并不会重复遍历。