机器学习——PCA(主成分分析)降维
PCA(主成分分析)降维详解
一、什么是 PCA
PCA(Principal Component Analysis,主成分分析)是一种常用的数据降维方法。它通过线性变换将原始的高维数据映射到低维空间,同时尽可能保留原数据的主要信息(即方差信息)。
一句话总结:
PCA 找到数据变化最大的方向,把数据投影到这些方向上,从而减少维度、压缩数据,同时降低冗余和噪声。
二、PCA 的主要作用
数据降维
减少特征数量,加快模型训练速度。降噪
去除方差较小、贡献不大的特征,减少噪声影响。特征提取
把原特征组合成新的主成分,减少相关性。可视化
将高维数据映射到二维或三维,方便绘图观察。
三、PCA 的核心思想
PCA 的核心思想是:
找到数据方差最大的方向(主成分方向)
将数据投影到这些方向上
选择前 k 个主成分作为新的特征空间
方差越大,表示数据在该方向的变化信息越多,保留它可以最大化信息量。
四、PCA 数学推导(简化版)
假设数据集为 X(已中心化):
计算协方差矩阵
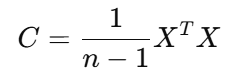
求特征值和特征向量
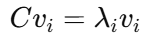
特征向量 vi 表示主成分方向
特征值 λi 表示方差大小
按特征值从大到小排序
取前 k 个特征向量组成投影矩阵 W降维
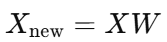
五、PCA 实现步骤
数据标准化(均值为 0,方差为 1)
计算协方差矩阵
求特征值和特征向量
选择前 k 个主成分
将数据投影到新空间
六、PCA 的优缺点
优点
降维有效,速度快
去除冗余特征,减少过拟合
对噪声有一定抑制作用
缺点
仅适用于线性降维
主成分是特征组合,不易解释含义
对特征缩放敏感,需要标准化
七、PCA 应用场景
图像压缩(如人脸识别中的特征提取)
高维数据可视化(如基因数据、股票数据)
机器学习前的数据预处理
八、PCA() 函数原型和参数表:
class sklearn.decomposition.PCA(n_components=None,*,copy=True,whiten=False,svd_solver='auto',tol=0.0,iterated_power='auto',n_oversamples=10,power_iteration_normalizer='auto',random_state=None
)
| 参数 | 类型 / 取值范围 | 默认值 | 作用说明 |
|---|---|---|---|
| n_components | int / float / 'mle' / None | None | - int:降到指定维度- float ∈ (0,1]:保留的累计方差比例(svd_solver='full' 时有效)- 'mle':自动估计最佳维度(svd_solver='full' 时)- None:保留 min(n_samples, n_features) 个主成分 |
| copy | bool | True | 是否在降维前复制数据,False 则在原数组上执行(可能修改原数据) |
| whiten | bool | False | 是否将输出的主成分缩放为单位方差(去相关+标准化),可能改变原数据的尺度含义 |
| svd_solver | 'auto' / 'full' / 'arpack' / 'randomized' / 'covariance_eigh' | 'auto' | - 'auto':自动选择- 'full':精确 SVD- 'arpack':截断 SVD(适合小规模特征子集)- 'randomized':随机近似 SVD(高维快)- 'covariance_eigh':特征值分解协方差矩阵(样本≫特征时快) |
| tol | float | 0.0 | SVD 收敛阈值(对迭代方法有效) |
| iterated_power | int / 'auto' | 'auto' | 随机 SVD 的迭代次数(通常保持默认) |
| n_oversamples | int | 10 | 随机 SVD 的过采样参数(svd_solver='randomized' 时) |
| power_iteration_normalizer | 'auto' / 'QR' / 'LU' / None | 'auto' | 随机 SVD 的幂迭代归一化方式 |
| random_state | int / RandomState / None | None | 随机种子(svd_solver='randomized' 时保证结果可复现) |
九、PCA Python 实战
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 使用微软雅黑字体
plt.rcParams['axes.unicode_minus'] = False # 处理负号显示异常# 1. 加载数据
iris = load_iris()
X = iris.data
y = iris.target# 2. 创建 PCA 模型(降到 2 维)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)# 3. 可视化
plt.figure(figsize=(8,6))
for target, color, label in zip([0,1,2], ['r','g','b'], iris.target_names):plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], c=color, label=label)plt.xlabel('主成分 1')
plt.ylabel('主成分 2')
plt.title('PCA 降维后的鸢尾花数据')
plt.legend()
plt.show()# 4. 方差贡献率
print("各主成分方差贡献率:", pca.explained_variance_ratio_)
# 输出结果:各主成分方差贡献率: [0.92461872 0.05306648]输出示例:
各主成分方差贡献率: [0.92461872 0.05306648]说明前两个主成分保留了约 97.7% 的信息。
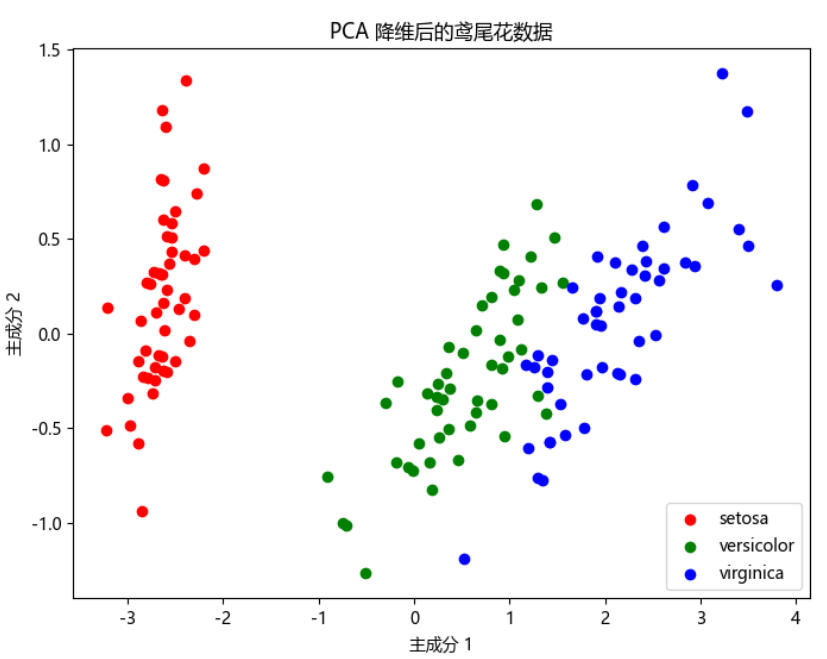
十、PCA 可视化原理
PCA 本质上是在找一组新的坐标轴(主成分轴),数据被重新投影到这些轴上,从而实现降维。
在二维图中,这些主成分轴相当于旋转后的新坐标系。
十一、总结
PCA 是通过最大化方差来提取主要特征的线性降维方法。
核心步骤是计算协方差矩阵 → 求特征值和特征向量 → 投影到主成分。
适合在特征数量大、存在相关性、需要可视化的场景使用。
