【题解|两种做法】[ZJOI2008] 洛谷 P2600 瞭望塔[半平面交]

前置知识：

半平面交相关知识

可以看看我超多图的半平面交笔记

题面：

洛谷 P2600

解析：

（1）半平面交做法

对于一个瞭望塔，一条线段上的任意位置都想被观测到，那瞭望塔必须在线段的上面。

我们想到了半平面交，把每条线段的上面当左边，所有线段跑一遍半平面交后会形成一个多边形。

（其实也可能是半个，没关系当成整个处理就行）

最开始还得加俩条边界线，防止多边形因为首尾边无限延伸导致答案错误。

瞭望塔肯定在多边形里及边上，我们从村子最左边的轮廓枚举一条与  轴平行的直线到右边。

看在什么时候直线经过的多边形轮廓上的点与村子轮廓上的点最近，输出两点距离就好。

可以发现，最优的方案之一一定经过多边形顶点或者村子顶点，所以只要枚举这些点就好。

（这个自己意会，尖尖角那些地方距离肯定小于等于线段的地方）

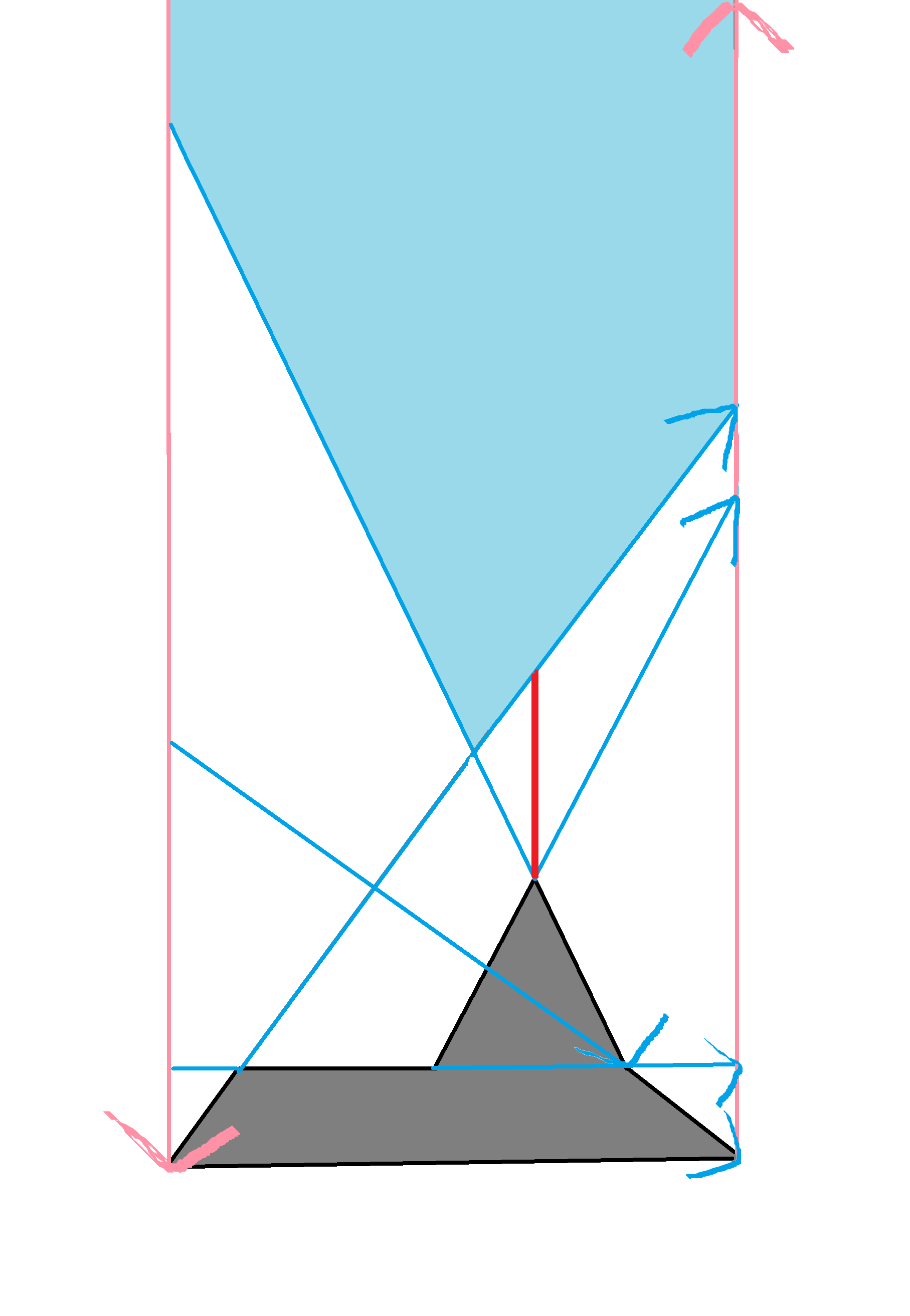
题面中的多边形：

黑色和灰色的是村庄，粉色的是边界线，天蓝色的是村庄边延伸，浅蓝色块是多边形。

加粗红色是最优方案，注意每个向量的有效被观测部分只有左边的平面。

有注释的代码：

（这题边界处理太复杂了，详细见注释，我很怀疑大多数题解边界处理的正确性）

（还有一些容易写错的细节我也特殊标记了，我调了好久。）

关于半平面交和原图村庄的点数问题，一般情况下半平面交点数是要小于等于原图的。

但我们加了俩边界线，点数会变多，所以就有可能大于原图。

当然还有那种很变态的锯齿图，半平面交一条直线可以交一堆点。

#include<bits/stdc++.h>
using namespace std;const int N = 310;
const double eps = 1e-12;
const double INF = 1e12;  //题解区有大佬说最大不会超过 5e11 struct point {double x, y;
} b[N], P[N];
struct line {point s, e;
} a[N], q[N];point operator+(point a, point b) {return {a.x + b.x, a.y + b.y};
}point operator-(point a, point b) {return {a.x - b.x, a.y - b.y};
}point operator*(point a, double t) {return {a.x * t, a.y * t};
}double operator*(point a, point b) {return a.x * b.y - a.y * b.x;
}double angle(line a) {return atan2(a.e.y - a.s.y, a.e.x - a.s.x);
}bool cmp(line a, line b) {double A = angle(a), B = angle(b);if (fabs(A - B) > eps) {return A < B;}else {return (a.e - a.s) * (b.e - a.s) < 0;}
}point cross(line a, line b) {point u = a.s - b.s;point v = a.e - a.s;point w = b.e - b.s;double t = (u * w) / (w * v);return a.s + v * t;
}bool right(line a, line b, line c) {point p = cross(b, c);return (a.e - a.s) * (p - a.s) <= 0;
}int n, m, len; double distance(point a, line b) {if ( (a.x < b.s.x) || (a.x > b.e.x) ) return INF;  //如果这个点的 x不在线段的范围内  //****不加上面这句话就会错*******//double y = (b.e.y - b.s.y) * ( (a.x - b.s.x) / (b.e.x - b.s.x) );  //用相似三角形算点到线段的距离 return fabs(y + b.s.y - a.y);
}void half_plane(){a[++n] = {{b[1].x , INF}, {b[1].x , -INF}}; //加个左边界 a[++n] = {{b[m].x , -INF}, {b[m].x , INF}}; //加个右边界 sort(a + 1, a + n + 1, cmp);int head = 1, tail = 1;q[1] = a[1];for (int i = 2; i <= n; i++) {if ((i!=1) && (angle(a[i]) - angle(a[i-1]) < eps)) continue;while (head < tail && right(a[i], q[tail - 1], q[tail])) {tail--;}while (head < tail && right(a[i], q[head], q[head + 1])) {head++;}tail++;q[tail] = a[i];}//加了左右边界就不用首尾相接 len = 0;for (int i = head; i < tail; i++) {len++;P[len] = cross(q[i], q[i + 1]);   //把多边形的顶点放进 P }double ans = INF;int vil = 1, pol = 1; while (vil <= m && pol <= len) {   //vil是村庄的顶点，pol是多边形的顶点 if (b[vil].x <= P[pol].x) {   //如果村庄点在多边形点的左边 if (pol > 1) {ans = min(ans, distance(b[vil], {P[pol-1], P[pol]}));  //让村庄点和多边形点的上一条边算距离 }if (vil < m) {ans = min(ans, distance(P[pol], {b[vil], b[vil+1]}));  //让多边形点和村庄点的下一条边算距离 }vil++;} else {                      //如果村庄点在多边形点的右边if (pol < len) {ans = min(ans, distance(b[vil], {P[pol], P[pol+1]}));  //让村庄点和多边形点的下一条边算距离 }if (vil > 1) {ans = min(ans, distance(P[pol], {b[vil-1], b[vil]}));  //让多边形点和村庄点的上一条边算距离 }pol++;}}//还有没处理完的情况//*****注意下面这段代码不能和上个 while混起来一起写！！会 RE*****//while (vil <= m) {if (pol > 1 && pol <= len) {ans = min(ans, distance(b[vil], {P[pol-1], P[pol]}));//为啥不用 ans = min(ans, distance(P[pol], {b[vil], b[vil+1]}))？ //因为这个 while没开始前的 vil才是离 P[pol] 最近的，后面的都没它优 }vil++;}while (pol <= len) {if (vil > 1 && vil <= m) {ans = min(ans, distance(P[pol], {b[vil-1], b[vil]}));//原因同上 }pol++;}cout << fixed << setprecision(3) << ans << endl;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> m;for (int i = 1; i <= m; i++) {cin >> b[i].x;}for (int i = 1; i <= m; i++) {cin >> b[i].y;}n = 0;for (int i = 1; i < m; i++) {n++;a[n] = {b[i], b[i + 1]};}half_plane();return 0;
}

（2）三分做法

其实本质是差不多的，也是构造出直线，然后用村庄点给多边形分段。

因为多边形的一段是下凹的一个角，相当于单峰函数，可以三分找出最低点。

（不会三分去问 AI，很简单的）

然后这个最低点还得代入每一条直线，如果点的 y 值小于直线上点 x 对应的 y 的值。

那直线 y 减去点 y 就是瞭望塔的高度，记录每一个最低点的高度，求最小。

（如果这个高度是负的，那就不用建塔，记录 ，最开始答案值设为  就好）

代码：

#include<bits/stdc++.h>
using namespace std;const int N = 310;
const double eps = 1e-7;
int n;struct point {double x, y;
} b[N];
struct line {double k, b;bool exit;   //判断这条直线是否有效 line() {exit = 0;}
} a[N];double calc(double x, double y) {double res = 0;for (int i = 1; i < n; i++) {  //这里注意直线只有 n-1条 if (a[i].exit == 0) continue;res = max( res, a[i].k * x + a[i].b - y );}return res;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;for (int i = 1; i <= n; i++) {cin >> b[i].x;}for (int i = 1; i <= n; i++) {cin >> b[i].y;}for(int i = 1; i < n; i++) {if (fabs(b[i].x - b[i + 1].x) < eps) continue;  //几乎平行 a[i].k = (b[i + 1].y - b[i].y) / (b[i + 1].x - b[i].x);a[i].b = b[i].y - a[i].k * b[i].x;a[i].exit = 1;}double ans = 1e20;for(int i = 1; i < n; i++) {  //这里注意直线只有 n-1条 if(a[i].exit == 0) continue;double L = b[i].x, R = b[i + 1].x;double mida, midb;int T = 100;while(T--) {mida = L + (R - L) / 3;midb = R - (R - L) / 3;double ta = calc(mida, mida * a[i].k + a[i].b);double tb = calc(midb, midb * a[i].k + a[i].b);if (ta < tb) {R = midb;}else {L = mida;}}	ans = min( ans, calc(mida, mida * a[i].k + a[i].b) ); //最后答案肯定在左边的 mida，可以自己模拟一下 }cout << fixed << setprecision(3) << ans << endl;return 0;
}

其实还有一种暴力做法，不过复杂度是错的，只是因为现在评测机跑得快 AC，这里就不放了。