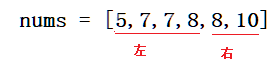专题三_二分_在排序数组中查找元素的第一个和最后一个位置

一：题目

解释：找值全为target的区间的开始和结束下标。所以target有可能只有一个值，此时的开始和结束下标是一致的！

本文称值为target的区间的开始位置为左端点，结束位置为右端点

二：算法

①：暴力

从左向右遍历数组找值为target的区间左端点，再从右往左遍历数组找值为target的区间的右端点，所以复杂度为O(N)，肯定是超时的，因为二分类型的题目，时间复杂度一定是O(logN)才能通过

②：朴素二分

朴素二分就是不断的找中点判断中点是否是某个值，但此题不在适用，因为即使你找到了target值，你也不确定是值为target区间的哪一个位置 ，所以你还得像左遍历找左端点，再向右遍历找右端点，这意味着若是遇到数组全是target的值，你的时间复杂度会退化为暴力的时间复杂度O(N)

③：优化二分

例子：nums = [5,7,7,8,8,10], target = 8  //下方例子，全部围绕此例子来讲解

优化二分的思路就是我们二分里面最重要的一句话，"具有二段性的数组，就可以使用二分！"

所以我们先找左端点，再找右端点，如果左端点不存在，则右端点也不用找了！因为左端点不存在，则证明数组根本无target，直接return{-1,-1}即可！

1：找左端点

所以我们可以将数组划分为两段去找左端点，我们现在找8的左端点，则数组分为以下两部分：

解释：此时数组就具有了二段性，可以使用二分来查找了！不断的求中点，然后判断中点值是<target还是>=target，根据不同的情况去移动left和right，最终双指针相遇，判断相遇处的值即可!

演示代码逻辑：

左部分<target，右部分>=target，所以当nums[mid]<8代表落入左，反之落入右部分，则：

nums[mid]<8：left=mid+1；//落入左部分

nums[mid]>=8：right=mid；//落入右部分

对left和right移动的解释：

你落入左部分，则代表此时的mid位置的值<8，则mid及mid往左的所有值都无意义(不可能有最终结果)，所以我们把left指针直接移动到了mid+1的位置

你落入右部分，则代表此时的mid位置的值>=8，则mid有可能就是左端点，也有可能不是左端点，所以right指针只能移动到了mid的位置！(mid-1不行，万一mid就是左端点呢！)

最后两者相遇，则相遇位置的值如果是target则是左端点，反之数组中无target值！

Q1：为什么这样就能保证双指针相遇？

A1：left一直在被mid+1，在最后一次left会跳出左部分，来到右部分的第一个元素，而right则最多刚好为右部分的左面，此时二者相遇！

Q2：为什么找左端点，就要这么划分？

A2：因为这样划分，当你双指针相遇的时候，通过对相遇处的值判断，要么就是左端点，要么不存在target值！如果你疑问为什么左部分不能含有一个8，如下：

这必然是错误的，此时代码逻辑找不到左端点不说，并且无法区分开左部分和右部分！

2：找右端点

右端点和左端点及其类似，但是右端点将数组分成了二段性稍有区别：

演示代码逻辑：

找右端点，则左部分<=8，右部分>8,当nums[mid]<=8代表落入左，反之落入右部分，则：

nums[mid]<=8：left=mid；//落入左部分

nums[mid]>8：right=mid-1；//落入右部分

3：细节

上面说了大题的思路，但是细节才是最重要的，任何细节只要写错，则死循环报错！

a：终止循环的写法

只有while(left<right)的写法才是对的！

Q：寻找端点的双指针循环条件为什么是left<right 而不是left<=right？

A：换句话说！两个指针相遇的时候，不能再次进入循环去判断！

所以我们要从left==right的时候，从不用再次进入循环，和需要再次进入循环，这两种做法，去对所有数组情况做演示来证明！

数组情况总共三种：

情况1：数组有答案

情况2：数组全<target

情况3：数组全>target

情况1：数组有答案

此时left ==right

不再循环：我们只需判断值是否为target即可，此时等于target，则找到左端点

再次循环：

发现nums[mid]的值为target，根据找左端点的代码逻辑，判定是右部分(>=target)，则进行right=mid。出错了！当right=mid之后，其实什么都没做，因为本来双指针相遇的位置就是mid！此时双指针依旧相等，则根据while(left<=right)又要找中点，陷入死循环！

情况2：数组全<target

此时left ==right

不再循环：我们只需判断值是否为target即可，此时不为target，则返回{-1,-1}

再次循环：

发现nums[mid]的值<target，根据找左端点的代码逻辑，则判定是左部分，则left=mid+1，此时left>right，成功跳出循环！

情况3：数组全>target

此时left ==right

不再循环：我们只需判断值是否为target即可

再次循环：

发现nums[mid]的值>target，根据找左端点的代码逻辑，判定是右部分>=target，则进行right=mid。出错了！当right=mid之后，其实什么都没做，因为本来双指针相遇的位置就是mid！此时双指针依旧相等，则根据while(left<=right)又要找中点，陷入死循环！

所以while(left<right)是正确的，while(left<=right)部分死循环！

总结：

当left==right的时候，我们不能进入循环，此时最佳做法是判断相遇处的值即可！若是进入循环，则一定无法通过此题！

b：求中点值写法

找左端点时求中点值写法是：left+(right-left)/2，反之找右端点为：left+(right-left+1)/2！

Q1：为什么找左端点时求中点值写法是：left+(right-left)/2？

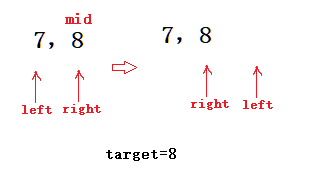
A1：如果用left+(right-left+1)/2的错误写法，假设现在只剩两个元素了，求出的mid是右面的元素，此时若是nums[mid]<target，则left=mid+1，会满足>=right，此时跳出while，正确！

如图：

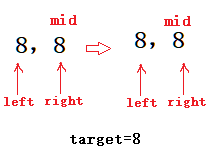
但是若是nums[mid]>=target，则right=mid，则right仍是原地踏步  会死循环，此时你的while里面尽管是正确的写法：left<right，依旧无济于事，因为你的left永远无法<=right去跳出循环！

如图：

Q2：为什么找右端点为：left+(right-left+1)/2？

同理！

A2：如果用left+(right-left)/2的错误写法，假设现在只剩两个元素了，求出的mid是左面的元素，此时若是nums[mid]>arget，则right=mid-1，会满足>=right，此时跳出while，正确！

但是若是nums[mid]<=target，则left=mid，会死循环！

本质：mid不能落到直接被mid赋值的指针！

找左端点中的right是直接被mid赋值，也就是right=mid，所以不能采取left+(right-left+1)/2，因为最后两个元素的时候，mid会落到right头上！导致死循环！

找右端点中的left是直接被mid赋值，也就是left=mid，所以不能采取left+(right-left)/2，因为最后两个元素的时候，mid会落到left头上！导致死循环！

总结：

左端点时求中点值写法必须为：left+(right-left)/2

左端点时求中点值写法必须为：left+(right-left+1)/2

三：代码

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {//对空数组的特判if (nums.empty())return {-1, -1};int left = 0, right = nums.size() - 1;int begin = -1;//找左端点while (left < right) {int mid = left + (right - left) / 2;//左段带你if (nums[mid] < target)left = mid + 1;elseright = mid;}//判断是否有左端点if (nums[left] != target)return {-1, -1};//来到这里 代表有左端点 则保存    begin = left;//找右端点right = nums.size() - 1;while (left < right) {int mid = left + (right - left + 1) / 2;if (nums[mid] <= target)left = mid;elseright = mid - 1;}//返回区间的起末下标return {begin, right};}
};

易错：

1：循环条件一定是left<right

2：找左端点中求中点值一定是left+(right-left)/2，反之右端点是left+(right-left+1)/2

3：找完左端点后，对相遇处的值判断，就能知道是否存在左端点，存在则才会去找右端点

4：找右端点可以直接让left从begin开始找，直接缩小了范围，不用再重置left=0

5：begin保存了左端点的下标后，在最后的返回阶段直接作为区间的左端点

四：模版

这种找一段区间的起始结束位置的题目的模版为：

找左端点：

while (left < right)
{
int mid = left + (right - left) / 2;
if (……) left = mid + 1;
else right = mid;
}

找右端点：

while (left < right)
{
int mid = left + (right - left + 1) / 2;
if (……)left = mid;
else right = mid - 1;

}

记忆：

1：双指针相遇不用再进入循环，所以left<right

2：找左端点，意味着左端点在右部分区间，所以left=mid+1想要跳到右部分区间和right相遇

3：找左端点求中点值，mid不能落在right=mid这种原地踏步指针上，所以left + (right - left) / 2;

4：找右端点，意味着右端点在左部分区间，所以right=mid-1想要跳到右部分区间和left相遇

5：找右端点求中点值，mid不能落在left=mid这种原地踏步指针上，所以left + (right - left+1) / 2;