Transformer 之自注意力机制(一)
Transformer 之自注意力机制(一)
文章目录
- Transformer 之自注意力机制(一)
- 一、自注意力机制
- 1. 产生背景
- 2. RNN、LSTM的问题
- 3. 解决问题
- 引入自注意力机制
- 4. 使用场景
- 5. 基本概念
- 5.1 核心目标
- 5.2 专业术语
- 5.3 句子标上 QKV(示例)
- 5.4 QKV的意义
- 二、自注意力机制实现过程
- 1. 词语关系
- 2. 线性变换
- 3. 查询-键-值(QKV)向量
- 3.1 查询向量 Q
- 3.2 键向量 K
- 3.3 值向量 V
- 3.4 注意力得分
- 3.5 归一化
- 3.6 加权求和
- 4. 案例
一、自注意力机制
1. 产生背景
自注意力源于序列建模(如翻译、生成)对长程依赖、并行效率的需求,RNN/LSTM 因梯度消失、串行计算而受限。
2. RNN、LSTM的问题
- RNN:梯度消失/爆炸,难捕捉长依赖。
- LSTM/GRU:门控缓解梯度,但仍串行,效率低。
共同痛点:长距依赖弱、计算串行、固定向量压缩致信息丢失。
3. 解决问题
先尝试 CNN,需深层堆叠,复杂度过高;遂提出自注意力。
引入自注意力机制
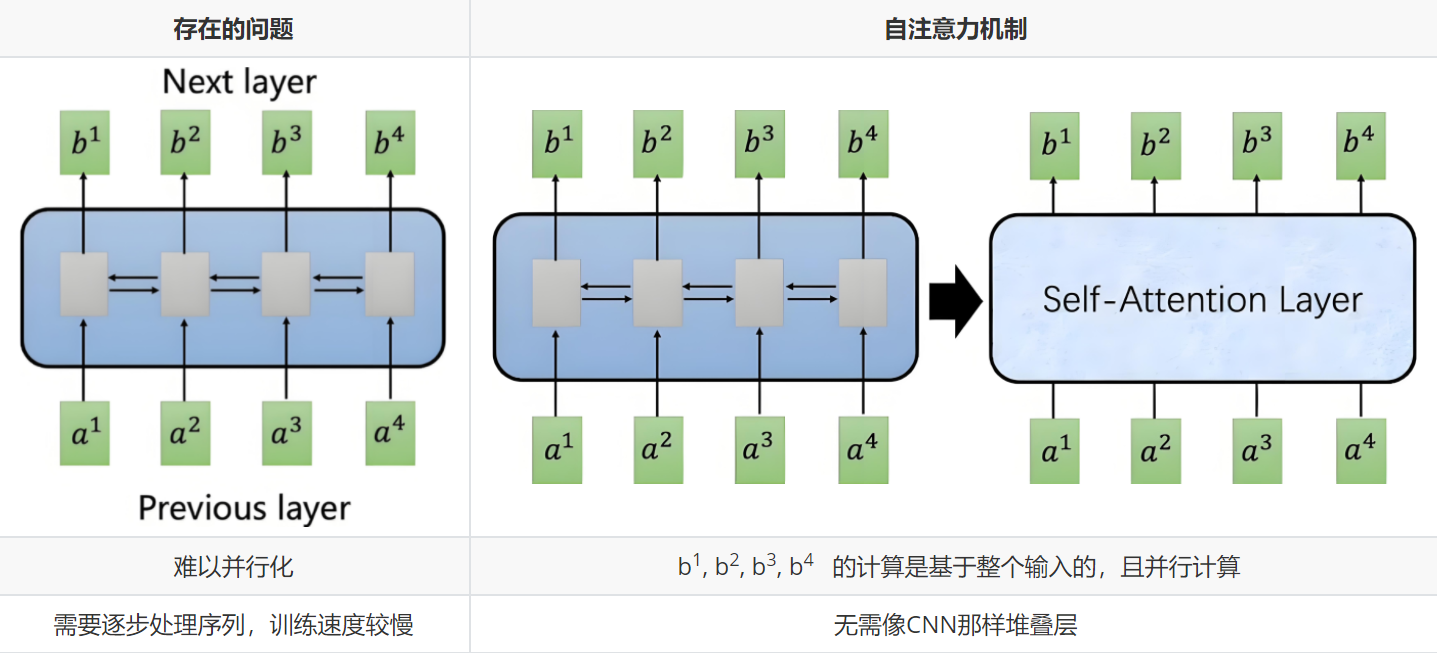
- 长距依赖:全局相关性一次捕获。
- 并行计算:整序列同时处理,速度提升。
- 动态权重:按重要性实时聚焦,无需固定上下文。
- 灵活输入:长度可变,结构无强制。
4. 使用场景
词义随上下文而变。例:
机器人第二法则
机器人必须服从人类给它的命令,除非该命令违背第一法则。
模型需通过上下文确定:
- 它=机器人
- 命令=人类给机器人的命令
- 第一法则=完整的第一法则内容
自注意力可一次性关联全句,完成上述指代消歧。
5. 基本概念
自注意力机制,就是找到自己和所在句子的所有的词之间的关联关系。
5.1 核心目标

自注意力的目标是让每个位置的表示能够根据整个序列中其他位置的信息进行加权融合,从而捕获实体之间的相互关系。
自注意力机制是要回答:“我(某个位置)应该关注谁(其他位置)?以及关注了之后该怎么融合信息?”
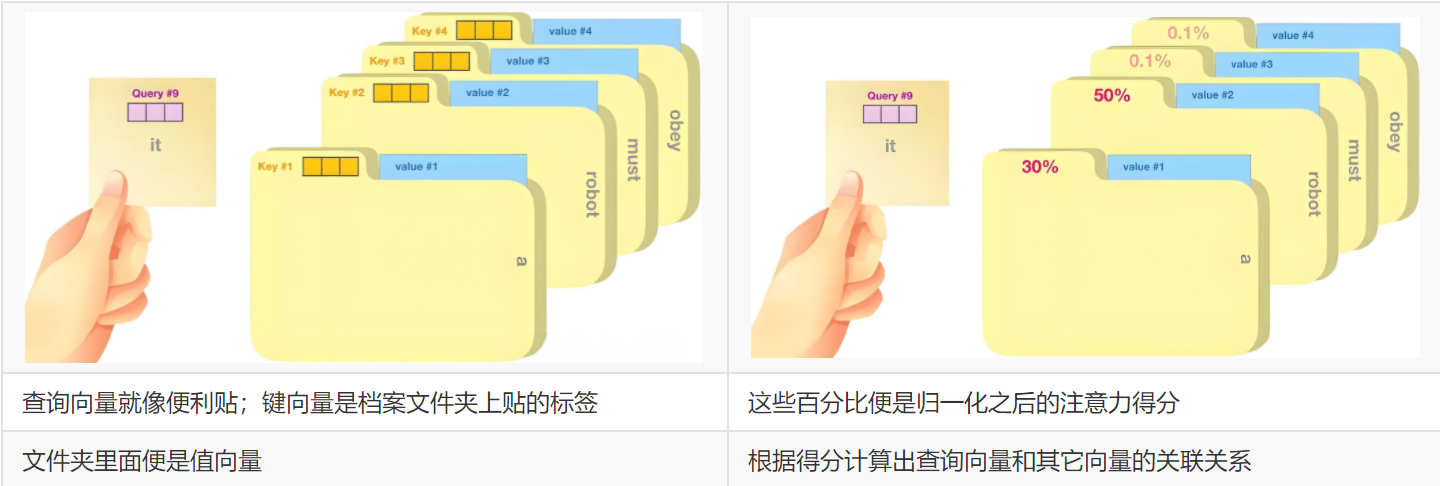
5.2 专业术语
自注意力机制通过引入查询向量(Query)、键向量(Key)、**值向量(Value)**概念来实现序列中各元素之间的信息交互和依赖建模。
-
Q:Query
表示当前查询者的位置,用来发出问题:“我想知道对我来说谁重要”。
-
K:Key
表示被查询者的身份,是所有位置给出的“介绍信”或“标签”,告诉别人自己是个啥玩意。
-
V:Value
表示被查询者实际信息,也就是一旦你决定“关注我了”,我就把这份信息给你。
5.3 句子标上 QKV(示例)
句子:「我是小明,是某某大学的一名学生,隶属于某某省份某某市。」
| Token | 角色 | 简要说明 |
|---|---|---|
| 我 | Q | 查询者:想知道“我”与谁相关 |
| 是 | K | 结构标签:提示句法关系 |
| 小明 | V | 实际信息:名字 |
| 是 | K | 标签:再次提示关系 |
| 某某大学 | V | 实际信息:学校名称 |
| 的 | K | 结构标签:修饰关系 |
| 一名 | K | 结构标签:数量 |
| 学生 | V | 实际信息:身份 |
| 隶属于 | K | 结构标签:隶属关系 |
| 某某省份 | V | 实际信息:省级区划 |
| 某某市 | V | 实际信息:市级区划 |
5.4 QKV的意义
序列中的每个 TokenTokenToken 都有 Q、K、VQ、K、VQ、K、V 三个角色:
- 所有位置之间需要【查询-响应】这样的互动,单一角色表达能力就太死板。
- “我该关注谁”是“我”和“他们”之间的交互过程,所以需要把“我”和“他们”分别建模(Q vs K)。
- 而最终融合的信息 VVV 可能和你打分 Q⋅KQ·KQ⋅K 的依据不完全相同,如:
- KKK :强调结构特征→【位置或语法角色】
- VVV: 强调语义内容→【单词的意义】
二、自注意力机制实现过程
1. 词语关系
it代表的是animal还是street呢,对我们来说简单,但对机器来说是很难判断的。self-attention就能够让机器把it和animal联系起来。
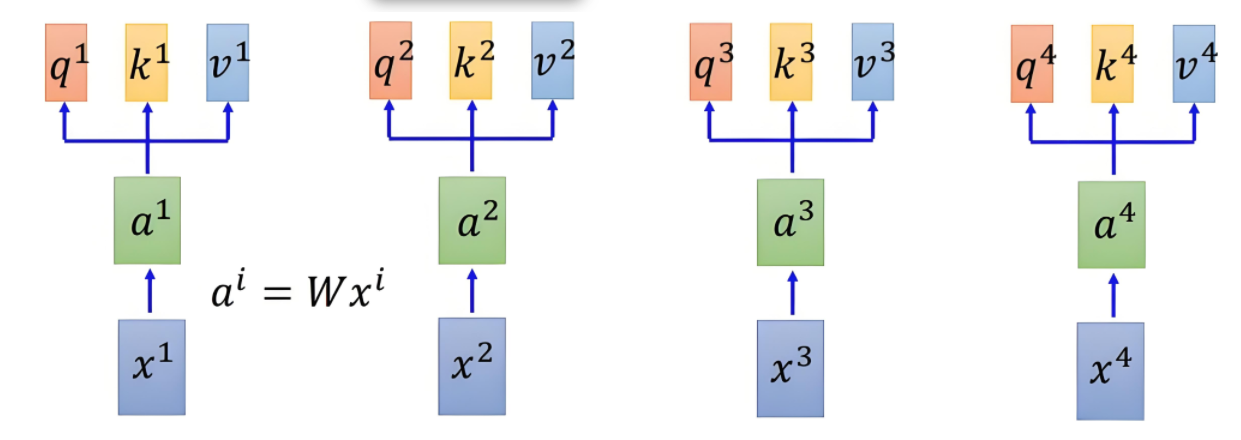
2. 线性变换
自注意力机制依赖于三个核心概念:查询向量Query、键向量Key、值向量Value。他们对输入 XXX 进行三次线性变换,得到三个矩阵。
3. 查询-键-值(QKV)向量
3.1 查询向量 Q
- 作用:当前词发出的“提问”——“其他词对我有多重要?”
- 计算:把输入词向量 X 乘可学习矩阵 W_q,得到 Q
Q=XWq,Wq∈Rd×dkQ = X \, W_q,\quad W_q\in\mathbb{R}^{d\times d_k}Q=XWq,Wq∈Rd×dk - 代码(保持维度不变,方便实现)
W_q = torch.randn(512, 512) # d = d_k = 512 Q = embedding_out @ W_q # [batch, seq_len, 512]
3.2 键向量 K
- 作用:每个词的“身份证”,供 Q 来匹配。
- 计算:同样用可学习矩阵 W_k
K=XWk,Wk∈Rd×dkK = X \, W_k,\quad W_k\in\mathbb{R}^{d\times d_k}K=XWk,Wk∈Rd×dk - 代码
W_k = torch.randn(512, 512) K = embedding_out @ W_k # [batch, seq_len, 512]
3.3 值向量 V
- 作用:真正要被提取的信息;注意力权重决定它有多少被采纳。
- 计算:
V=XWv,Wv∈Rd×dv(一般dv=dk)V = X \, W_v,\quad W_v\in\mathbb{R}^{d\times d_v}\;(一般 d_v=d_k)V=XWv,Wv∈Rd×dv(一般dv=dk) - 代码
W_v = torch.randn(512, 512) V = embedding_out @ W_v # [batch, seq_len, 512]
小结:每个词同时扮演“提问者(Q)”、“身份证(K)”和“信息源(V)”三重角色,通过矩阵乘法一次性生成,随后进入注意力权重计算与加权求和。
3.4 注意力得分
使用点积来计算查询向量和键向量之间的相似度,除以缩放因子 dk\sqrt{d_k}dk 来避免数值过大,使得梯度稳定更新。得到注意力得分矩阵:
Attention(Q,K)=QKTdk\text{Attention}(Q, K) = \frac{QK^T}{\sqrt{d_k}} Attention(Q,K)=dkQKT
参考代码如下:
# 计算原始的注意力得分score = torch.matmul(Query, Key.transpose(0, 1)) / math.sqrt(512)print(score)
参考示意图如下:
注意力得分矩阵维度是 n×nn \times nn×n,其中 nnn 是序列的长度。每个元素 (i,j)(i, j)(i,j) 表示第 iii 个元素与第 jjj 个元素之间的相似度。
参考示意图如下:
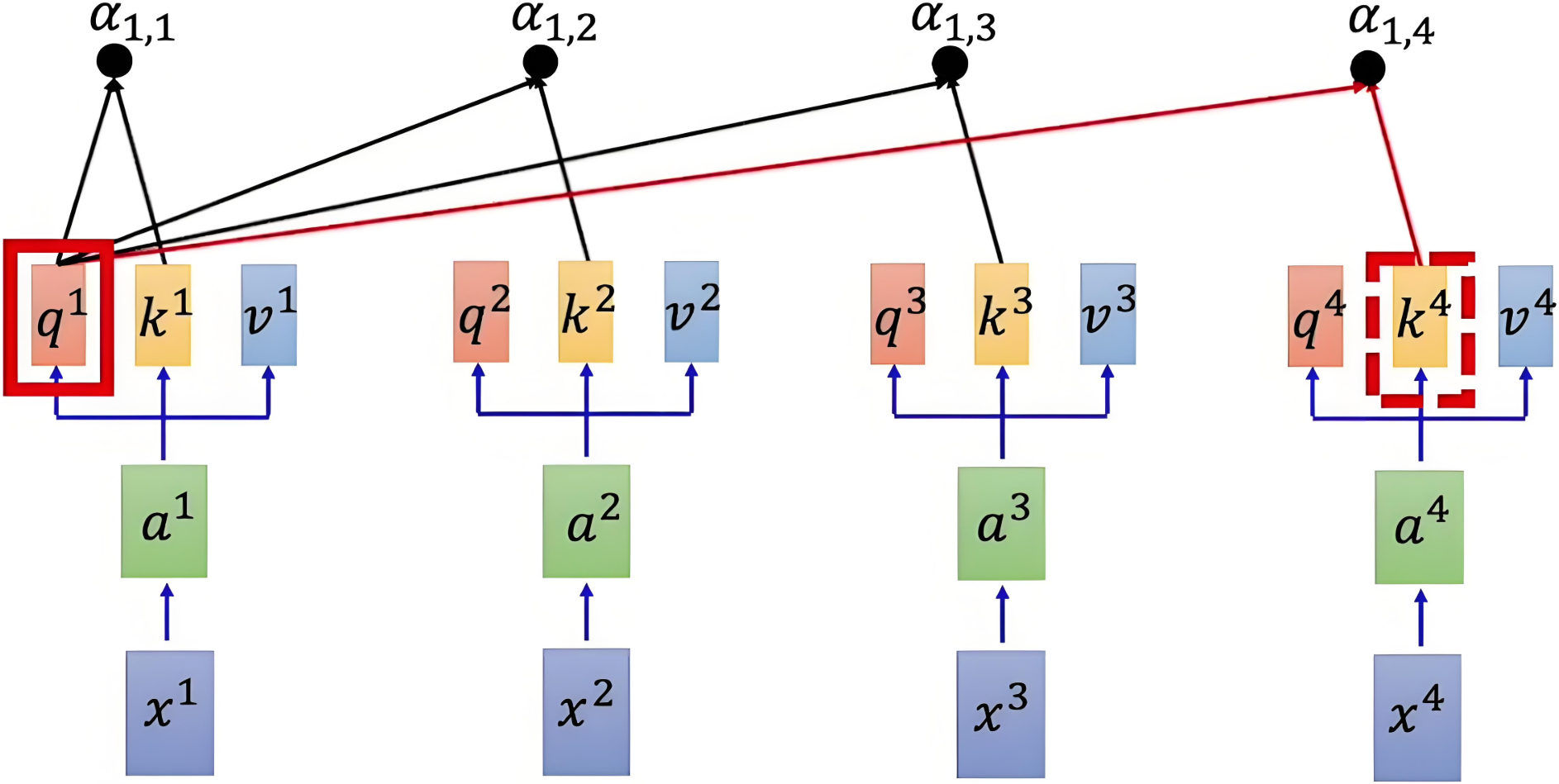 |
|---|
| α1,i=q1⋅kidk\alpha_{1,i} = \dfrac{q^1 \cdot k^i}{\sqrt{d_k}}α1,i=dkq1⋅ki |
3.5 归一化
为了将注意力得分转换为概率分布,需按行对得分矩阵进行 softmaxsoftmaxsoftmax 操作,确保每行的和为 1,得到的矩阵表示每个元素对其他元素的注意力权重。是的,包括自己。
Attention Weight=softmax(QKTdk)\text{Attention Weight} = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) Attention Weight=softmax(dkQKT)
具体到每行的公式如下:
α^1,i=exp(α1,i)∑jexp(α1,j)\hat{\alpha}_{1,i} = \frac{\exp(\alpha_{1,i})}{\sum_j \exp(\alpha_{1,j})} α^1,i=∑jexp(α1,j)exp(α1,i)
- α1,i\alpha_{1,i}α1,i :第 111 个词语和第 iii 个词语之间的原始注意力得分。
- α^1,i\hat{\alpha}_{1,i}α^1,i :经过归一化后的注意力得分。
参考代码如下:
# 注意力得分归一化normalized_scores = F.softmax(scores, dim=1)print(normalized_scores)
注:一行上进行归一化
3.6 加权求和
通过将注意力权重矩阵与值矩阵 VVV 相乘,得到加权的值表示。
Output=Attention Weight×V=softmax(QKTdk)×V\text{Output} =\text{Attention Weight} \times V = \text{softmax} \left( \frac{QK^T}{\sqrt{d_k}} \right) \times V Output=Attention Weight×V=softmax(dkQKT)×V
具体计算示意图如下:
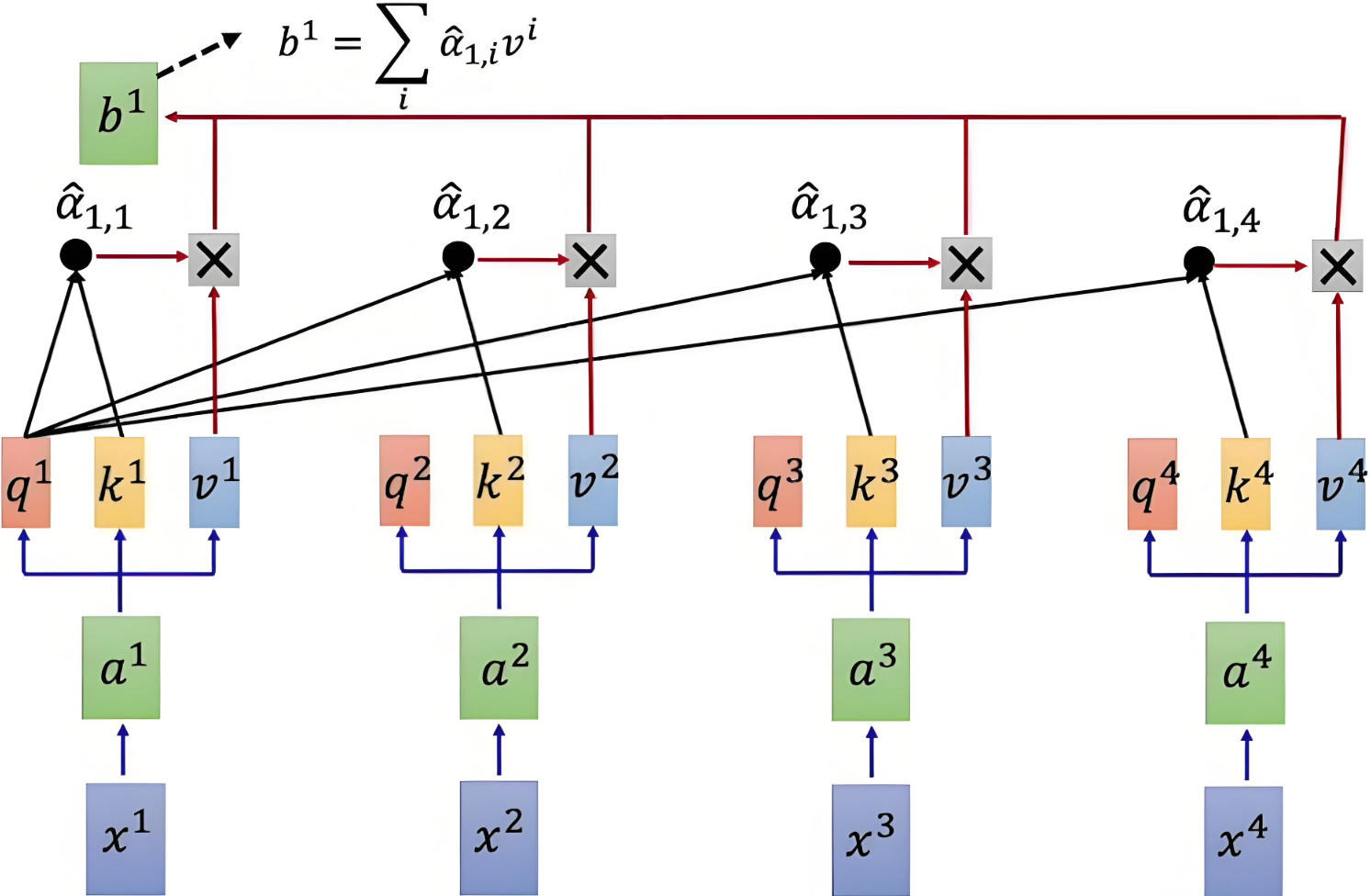 |
|---|
| Q和K计算相似度后,经 softmaxsoftmaxsoftmax 得到注意力,再乘V,最后相加得到包含注意力的输出 |
参考代码如下:
# 加权求和获取注意力后的结果attention_result = torch.matmul(normalized_scores, Value)print(attention_result.shape) # torch.Size([7, 512])
注:通过上下文来描述每一个词
4. 案例
import torch
import torch.nn as nn# 1. 数据准备
sentences = ["i am an NLPer"]# 2. 词表 & 索引
vocab = sorted({w for sent in sentences for w in sent.split()})
word2idx = {w: i for i, w in enumerate(vocab)}
indices = torch.tensor([[word2idx[w] for w in sent.split()] for sent in sentences],dtype=torch.long)
# [batch, seq_len]
# 3. Embedding
dim = 256
embedding = nn.Embedding(len(vocab), dim)
x = embedding(indices) # [1, 4, 256]# 4. 生成 Q、K、V(共享输入,但各自独立线性映射)
W_q = nn.Linear(dim, dim)
W_k = nn.Linear(dim, dim)
W_v = nn.Linear(dim, dim)Q = W_q(x) # [1, 4, 256]
K = W_k(x) # [1, 4, 256]
V = W_v(x) # [1, 4, 256]# 5. 计算注意力权重
d_k = dim
scores = torch.matmul(Q, K.transpose(-2, -1)) / (d_k ** 0.5) # [1, 4, 4]
attn_weights = torch.softmax(scores, dim=-1) # [1, 4, 4]# 6. 加权求和得到输出
out = torch.matmul(attn_weights, V) # [1, 4, 256]print("输入形状: ", x.shape)
print("输出形状: ", out.shape)
运行结果示例
输入形状: torch.Size([1, 4, 256])
输出形状: torch.Size([1, 4, 256])
这样就完成了一个单头自注意力的极简实现:
- 通过线性层把同一输入映射成 Q、K、V;
- 计算注意力分数并 softmax;
- 用权重对 V 做加权求和。
