C++ 优选算法 力扣 209.长度最小的子数组 滑动窗口 （同向双指针）优化 每日一题 详细题解

一、题目描述

题目链接：长度最小的子数组

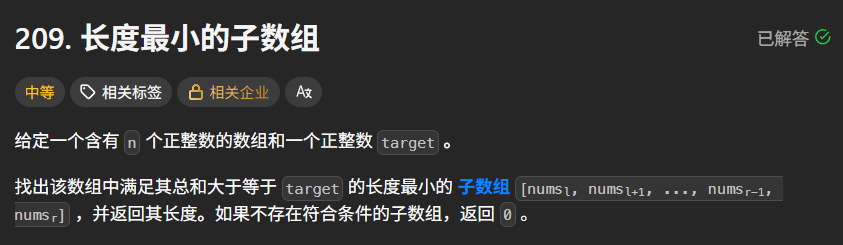
题目描述：

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 的和是 7，长度最小。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1
解释：子数组 [4] 的和是 4，长度最小。

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0
解释：没有和≥11的子数组，返回0。

提示：
1 <= target <= 10^9
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5

二、为什么这道题值得你花几分钟看懂？

长度最小的子数组作为 LeetCode 第 209 题，是 滑动窗口（双指针）算法的经典入门题，几乎是算法面试中“子数组问题”的必考点。它的核心价值在于：

• 帮你理解 “如何将暴力解法的 O(n²) 甚至 O(n³) 复杂度优化到 O(n)”，这是算法效率提升的关键思维；
• 掌握 “动态维护区间”的核心套路，这种思路能解决一大类子数组/子串问题（如最小覆盖子串、水果成篮等）；
• 深刻理解 “单调性”在算法优化中的作用——正是因为数组元素为正整数，才能用滑动窗口实现高效收缩。

学会这道题，你能举一反三解决：

• 最小覆盖子串（LeetCode 76）
• 水果成篮（LeetCode 904）
• 最长连续递增序列（LeetCode 674）等问题

生活中也有类似场景，比如“流量监控中找到持续超标的最短时间段”“电商订单中找到累计金额达标的最短购买序列”，核心都是“在连续区间中找满足条件的最小长度”。

三、题目拆解：提取其中的关键点

结合问题要求和代码框架，核心要素如下：

1. 输入是正整数数组 nums 和正整数 target，数组长度可达 10⁵（需考虑效率）。
2. 需找到连续子数组（元素在数组中连续排列），其和≥ target，且长度最小。
3. 若不存在这样的子数组，返回 0。

关键点提炼：

• 连续性：子数组元素必须连续（区别于子序列）。
• 单调性：数组元素为正整数 → 子数组长度增加时，和一定增大（这是滑动窗口的核心依据）。
• 高效性：暴力解法会超时，需优化到 O(n) 时间复杂度。
• 边界处理：不存在有效子数组时返回 0。

四、明确思路：从暴力到滑动窗口

1. 暴力解法的困境
最直观的思路是枚举所有可能的连续子数组，计算其和并判断是否≥target，记录最小长度。

• 三层循环版本：
  外层循环枚举子数组起点 i（0≤i<n），中层循环枚举子数组终点 j（i≤j<n），内层循环计算 i 到 j 的和。时间复杂度 O(n³)，在 n=10⁵ 时完全不可行。

• 优化的二层循环：
  用前缀和优化求和过程（提前计算前缀和数组 preSum，则 i 到 j 的和为 preSum[j+1]-preSum[i]），时间复杂度降至 O(n²)。但 n=10⁵ 时，10¹⁰ 次操作仍会超时。

结论：必须找到 O(n) 级别的算法。

2. 滑动窗口的核心：利用单调性优化
为什么能用滑动窗口？
数组元素都是正整数 → 子数组的和具有单调性：

• 当窗口右边界 right 右移时，窗口内元素增加，和一定增大；
• 当窗口左边界 left 右移时，窗口内元素减少，和一定减小。

这种单调性让我们可以用双指针维护窗口，避免重复计算。

滑动窗口的思路

• 用 left 和 right 标记窗口的左右边界，初始都为 0。
• 先移动 right 扩大窗口，累加元素和 sum，直到 sum ≥ target。
• 此时尝试移动 left 缩小窗口：记录当前窗口长度（right-left+1），然后 sum 减去 nums[left]，left 右移，直到 sum < target。
• 重复上述过程，更新最小长度。

为什么这样正确？
当 [left, right] 满足 sum ≥ target 时：

• 任何包含 [left, right] 的更大窗口（如 [left, right+1]）长度更长，不可能是最小解，因此无需考虑；
• 缩小窗口（left 右移）可能得到更短的有效窗口（如 [left+1, right]），因此需要尝试收缩。

由于 right 和 left 都只向右移动（不会回退），每个元素最多被访问 2 次，时间复杂度降至 O(n)。

五、算法实现：滑动窗口（双指针）

核心逻辑：

1. 初始化 sum=0（当前窗口和）、len=INT_MAX（最小长度）、left=0（左边界）。
2. 右指针 right 从 0 遍历数组，每次将 nums[right] 加入 sum。
3. 当 sum ≥ target 时：
   • 计算当前窗口长度 right-left+1，更新 len 为最小值。
   • 收缩左边界：sum 减去 nums[left]，left 右移，直到 sum < target。
4. 遍历结束后，若 len 仍为 INT_MAX，返回 0；否则返回 len。

六、C++代码实现：一步步拆解

完整代码（附详细注释）：

#include <vector>
#include <climits>  // 包含INT_MAX
using namespace std;class Solution {
public:int minSubArrayLen(int target, vector<int>& nums) {int sum = 0;          // 当前窗口的和int len = INT_MAX;    // 最小长度，初始化为最大值int size = nums.size();// left：窗口左边界，right：窗口右边界for (int left = 0, right = 0; right < size; right++) {sum += nums[right];  // 右移右边界，扩大窗口，累加和// 当窗口和≥target时，尝试收缩左边界while (sum >= target) {// 更新最小长度：当前窗口长度为right-left+1len = min(len, right - left + 1);// 收缩左边界：减去左元素，left右移sum -= nums[left++];}}// 若未找到有效子数组，返回0；否则返回最小长度return len == INT_MAX ? 0 : len;}
};

代码拆解

1. 初始化

int sum = 0;          // 记录当前窗口[left, right]的元素和
int len = INT_MAX;    // 用INT_MAX表示“未找到有效子数组”，方便后续比较
int size = nums.size();

2. 右指针遍历与窗口扩大

for (int left = 0, right = 0; right < size; right++) {sum += nums[right];  // 每次右指针右移，将新元素加入窗口// ... 收缩左边界的逻辑 ...
}

• right 从 0 到 size-1 遍历，确保每个元素都被考虑作为窗口右边界。
• sum 实时累加当前窗口的和，避免重复计算（这是比暴力法高效的关键）。

3. 左指针收缩与更新最小长度

while (sum >= target) {  // 只要窗口和满足条件，就尝试收缩左边界len = min(len, right - left + 1);  // 更新最小长度sum -= nums[left++];  // 移除左边界元素，左指针右移
}

• 循环条件：sum ≥ target 保证只在有效窗口内收缩，一旦不满足则停止。
• 长度计算：right - left + 1 是当前窗口的长度（连续子数组的长度）。
• 收缩操作：sum -= nums[left++] 等价于先移除 nums[left]，再将 left 右移，实现窗口左边界收缩。

示例运行过程（以示例 1 为例）
输入：target = 7，nums = [2,3,1,2,4,3]

1. right=0（nums[0]=2）：sum=2 <7 → 继续。
2. right=1（nums[1]=3）：sum=5 <7 → 继续。
3. right=2（nums[2]=1）：sum=6 <7 → 继续。
4. right=3（nums[3]=2）：sum=8 ≥7 → 进入循环：
   • len = min(INT_MAX, 3-0+1)=4；
   • sum=8-2=6（left=1），sum<7 → 退出循环。
5. right=4（nums[4]=4）：sum=6+4=10 ≥7 → 进入循环：
   • len = min(4, 4-1+1)=4；
   • sum=10-3=7（left=2），仍≥7 → len=min(4,4-2+1)=3；
   • sum=7-1=6（left=3），sum<7 → 退出循环。
6. right=5（nums[5]=3）：sum=6+3=9 ≥7 → 进入循环：
   • len = min(3,5-3+1)=3；
   • sum=9-2=7（left=4），仍≥7 → len=min(3,5-4+1)=2；
   • sum=7-4=3（left=5），sum<7 → 退出循环。

最终 len=2，返回 2，符合示例结果。

时间复杂度

• O(n)：right 和 left 都只从 0 移动到 n-1，每个元素最多被访问 2 次（一次被 right 加入，一次被 left 移除）。

空间复杂度

• O(1)：仅使用常数个额外变量（sum、len、left、right），未使用额外空间。

七、实现过程中的坑点总结

1. 初始值设置错误

   • 错误写法：len 初始化为 0 或 nums.size()+1。
   • 问题：若初始为 0，可能无法更新为正确的最小长度；若初始为 nums.size()+1，当数组长度为 10⁵ 时可能溢出。
   • 解决：用 INT_MAX（最大整数）作为初始值，既方便比较最小值，又能通过是否等于 INT_MAX 判断是否存在有效子数组。

2. 忽略“无有效子数组”的情况

   • 错误写法：直接返回 len。
   • 问题：当所有子数组和都 < target 时，len 仍为 INT_MAX，返回错误结果。
   • 解决：返回前判断 len == INT_MAX，是则返回 0，否则返回 len。

3. 数组元素非正整数的误区

   • 错误假设：滑动窗口适用于所有子数组和问题。
   • 问题：若数组包含 0 或负数，和的单调性被打破（窗口扩大时和可能不变或减小），滑动窗口逻辑失效。
   • 注意：本题能使用滑动窗口的前提是数组元素为正整数，解题时需确认这一条件。

4. 求和溢出风险

   • 潜在问题：当 nums 元素很大（如 10⁵ 个 10⁹），sum 可能超过 int 范围（2¹⁴⁷⁴⁸³⁶⁴⁷）。
   • 解决：用 long long 存储 sum：long long sum = 0;（题目中虽未明确，但工业级代码需考虑）。

八、什么时候用滑动窗口？

滑动窗口（双指针）适用于连续区间问题，且满足以下条件：

1. 区间具有单调性：如和、积、频次等随窗口扩大/缩小呈现规律性变化（本题因正整数保证和的单调性）。
2. 需寻找区间的极值：如最小长度、最大长度、特定和等。
3. 避免重复计算：暴力法中存在大量重复计算的区间（如本题中 [i,j] 和 [i,j+1] 有重叠元素）。

常见应用场景：

• 子数组/子串的和、积、长度相关问题；
• 字符串匹配（如最小覆盖子串）；
• 区间内元素频次统计（如水果成篮）。

九、举一反三

掌握滑动窗口后，可解决以下问题：

• LeetCode 76. 最小覆盖子串：在字符串 S 中找包含 T 所有字符的最短子串，核心是用滑动窗口维护字符频次。
• LeetCode 904. 水果成篮：找只包含两种元素的最长连续子数组，用滑动窗口维护元素种类，我记得上周的力扣就是水果问题一言难尽/(ㄒoㄒ)/~~。
• LeetCode 643. 子数组最大平均数 I：找长度为 k 的子数组的最大平均数，用滑动窗口固定长度求和。

核心规律：滑动窗口的本质是用双指针维护一个动态区间，通过边界的单向移动避免重复计算，将 O(n²) 优化为 O(n)。

十、下题预告

明天将讲解 LeetCode 3. 无重复字符的最长子串，这道题是滑动窗口在字符串问题中的经典应用。它的核心是用窗口维护“无重复字符”的区间，并用哈希表记录字符位置以快速收缩窗口。与今天的题目相比，它的窗口收缩逻辑更复杂（需根据重复字符位置调整左边界），敬请期待！

如果觉得这篇解析有帮助，不妨：
🌟 点个赞，让更多人看到这份清晰思路
⭐ 收个藏，下次复习时能快速找回灵感
👀 加个关注，明天的字符串滑动窗口解析更精彩～

这是封面原图：