力扣top100(day02-05)--二叉树 02
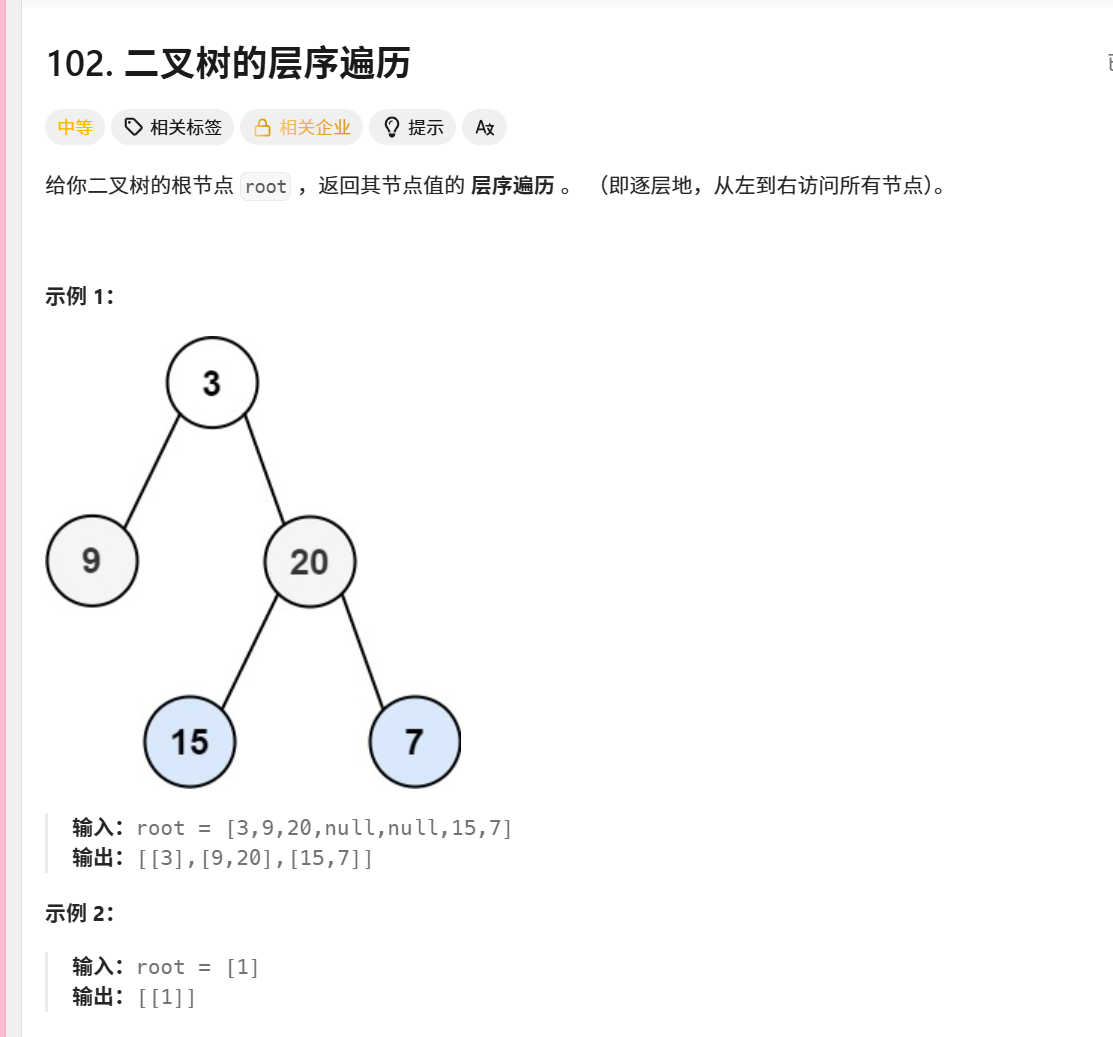
102. 二叉树的层序遍历

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {// 创建结果列表,用于存储每层的节点值List<List<Integer>> ret = new ArrayList<List<Integer>>();// 处理空树情况if (root == null) {return ret;}// 创建队列用于BFS遍历,初始时加入根节点Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root); // 将根节点加入队列// 开始BFS遍历while (!queue.isEmpty()) {// 创建当前层的节点值列表List<Integer> level = new ArrayList<Integer>();// 记录当前层的节点数量int currentLevelSize = queue.size();// 遍历当前层的所有节点for (int i = 1; i <= currentLevelSize; ++i) {// 从队列头部取出一个节点TreeNode node = queue.poll();// 将节点值加入当前层列表level.add(node.val);// 将该节点的子节点加入队列(先左后右)if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}// 将当前层的节点值列表加入结果列表ret.add(level);}// 返回层序遍历结果return ret;}
}关键点说明
BFS(广度优先搜索)算法:
使用队列数据结构实现
从根节点开始,按层级依次遍历
层序遍历的特点:
每层节点单独存储在一个子列表中
结果是一个二维列表,每个子列表代表一层的节点值
队列的使用:
offer()方法用于将元素加入队列尾部
poll()方法用于从队列头部取出元素时间复杂度:
O(n):每个节点被访问一次
n为二叉树中的节点总数
空间复杂度:
O(n):最坏情况下队列需要存储所有叶子节点
示例执行流程
对于如下二叉树:
text
3/ \9 20/ \15 7执行过程:
初始队列:[3]
处理3,加入子列表[3]
加入子节点9,20 → 队列:[9,20]
处理队列:[9,20]
处理9 → 子列表[9](无子节点)
处理20 → 子列表[9,20]
加入子节点15,7 → 队列:[15,7]
处理队列:[15,7]
处理15 → 子列表[15](无子节点)
处理7 → 子列表[15,7](无子节点)
最终结果:[[3], [9,20], [15,7]]
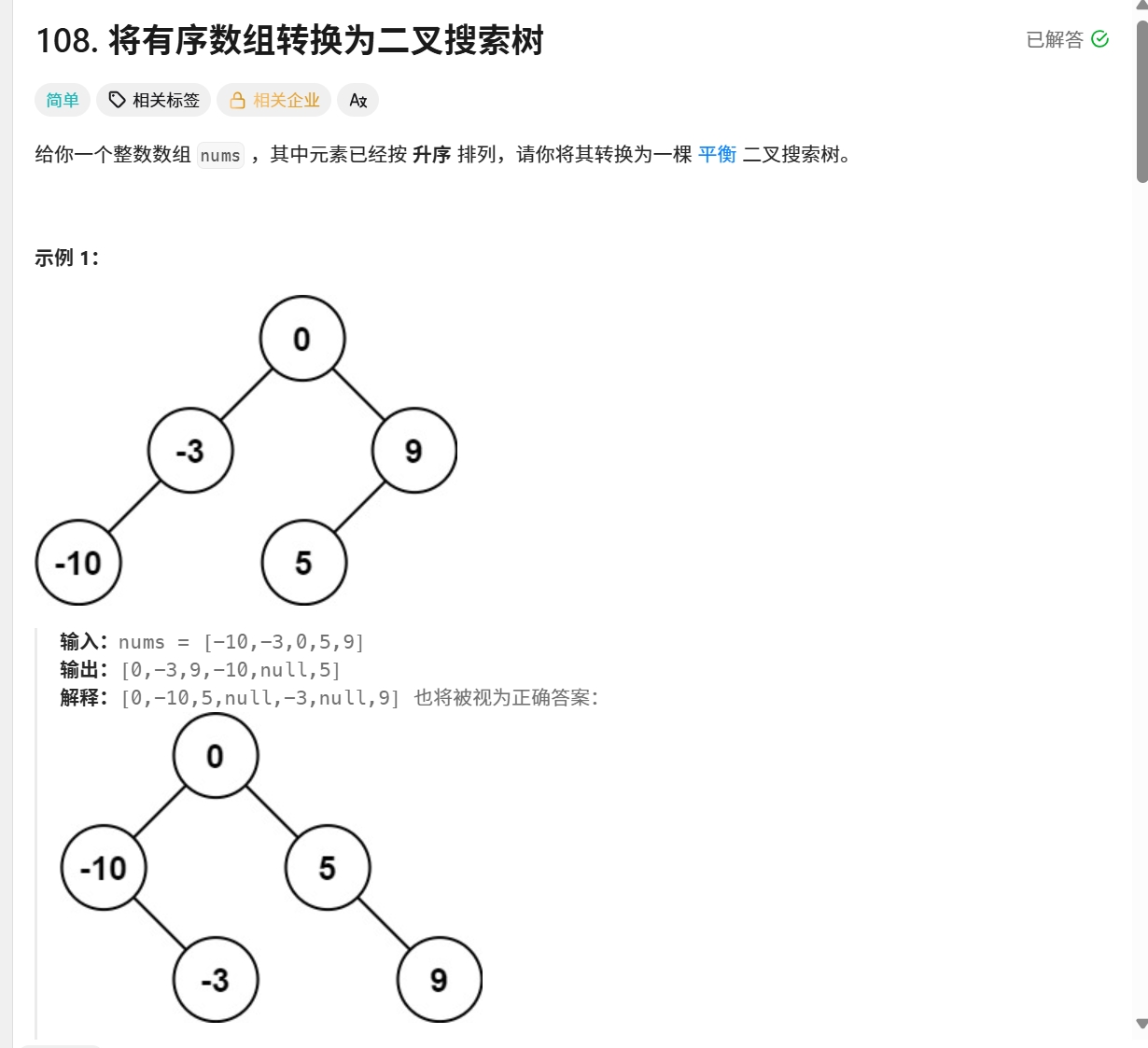
108. 将有序数组转换为二叉搜索树

/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode sortedArrayToBST(int[] nums) {return helper(nums, 0, nums.length - 1);}public TreeNode helper(int[] nums,int left, int right){if(left>right){return null;}int tip=(left+right)/2;TreeNode root = new TreeNode(nums[tip]);root.left=helper(nums, left, tip-1);root.right=helper(nums,tip+1,right);return root;}
}/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
/**
* 将有序数组转换为高度平衡的二叉搜索树
* @param nums 有序整数数组
* @return 二叉搜索树的根节点
*/
public TreeNode sortedArrayToBST(int[] nums) {
// 调用辅助函数,传入数组和初始边界
return helper(nums, 0, nums.length - 1);
}
/**
* 递归辅助函数,构建BST
* @param nums 有序数组
* @param left 当前子数组的左边界
* @param right 当前子数组的右边界
* @return 构建好的子树根节点
*/
public TreeNode helper(int[] nums, int left, int right) {
// 递归终止条件:左边界超过右边界
if (left > right) {
return null;
}
// 选择中间位置作为当前子树的根节点
// 这样能保证树的高度平衡
int mid = (left + right) / 2;
// 创建当前根节点
TreeNode root = new TreeNode(nums[mid]);
// 递归构建左子树(使用左半部分数组)
root.left = helper(nums, left, mid - 1);
// 递归构建右子树(使用右半部分数组)
root.right = helper(nums, mid + 1, right);
return root;
}
}
关键点说明
高度平衡BST的定义:
每个节点的左右子树高度差不超过1
通过总是选择中间元素作为根节点来保证平衡性
分治算法思想:
将问题分解为更小的子问题(左子树和右子树)
合并子问题的解(构建当前树)
时间复杂度:
O(n):每个元素只被访问一次
n为数组长度
空间复杂度:
O(log n):递归栈的深度
对于平衡BST,树的高度为log n
中间位置选择:
mid = (left + right) / 2对于偶数长度数组,可以选择中间偏左或偏右这里选择的是偏左的位置(因为整数除法会截断小数)
示例执行流程
对于输入数组:[-10, -3, 0, 5, 9]
构建过程:
初始调用:helper(nums, 0, 4)
mid=2 → root=0
左子树:helper(nums, 0, 1)
mid=0 → root=-10
左子树:helper(nums, 0, -1) → null
右子树:helper(nums, 1, 1)
mid=1 → root=-3
左右子树均为null
右子树:helper(nums, 3, 4)
mid=3 → root=5
左子树:helper(nums, 3, 2) → null
右子树:helper(nums, 4, 4)
mid=4 → root=9
左右子树均为null
最终BST结构:
text
0/ \-10 5\ \-3 9算法变体
选择中间偏右的位置:
java
int mid = (left + right + 1) / 2;对于偶数长度数组会选择中间偏右的元素
迭代实现:
可以使用栈来模拟递归过程,避免递归调用处理大数据集:
对于非常大的数组,可以考虑将数组分段处理这种实现方式充分利用了有序数组和二叉搜索树的特性,通过分治策略高效地构建出平衡的二叉搜索树。
