各种排序算法(二)
借助上文的势头我们来完成今天这篇小文章:

第二部分:复杂排序:
1.1 希尔排序:
希尔排序就是对插入排序的进化,我们发现插入排序还是太慢了,在希尔的思路想法下,我们可以先尝试预排:我们先进行分组,没间隔gap为一组,这样就分成了gap组了,不如gap = 3,那么就分成了3组,这样做的好处就是可以让大的快速到后面去,小的能够快速到前面去。这真的是一个很厉害的思想,有了这样的思想,我们就可以改进我们的插入排序:
void ShellSort(int* a,int n)
{//对于希尔排序的区别就是 gap的值有所变化,先进行预排序//先写第一趟int gap = 3;while (gap){//但是我们还要进行完成希尔排序,还要一层循环for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap)//将j赋值给i后可以控制每组的预排{int end = i;//end 的值不知道的话先不确定int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){//如果比他小,我们就要把 end的值往 end+gap 移动,end还需要再减 gapa[end + gap] = a[end];end = end - gap;}else {//说明和他相等或者比他大break;}}a[end + gap] = tmp;//把 tmp的值加进去}}gap--;
}
笔者在写这一段代码时候我也很难受,主要是还是挺难的,我们进行不断拆分:先想成了gap = 3,对里面进行第一次预排,最里面的循环就只完成了一组,在通过j来控制3组,最后在通过gap来控制gap–,来往希尔排序,这里只是初步的排序,还是不太好看,也不符合真正的希尔排序,我们还要继续进行改进:
void ShellSort(int* a, int n)
{//我们结合上面的第一版来进行改善int gap = n;while (gap > 1){gap = gap / 3 + 1;//原本是有一个循环控制 gap组的预排,现在直接同时排序for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else {break;}}a[end + gap] = tmp;}}
}
讲一下为什么选择/3+ 1,主要是大部分教材都是这样的,我们来看:
快速缩小增量
-
gap / 3:相比传统的折半(gap / 2),除以 3 能更快缩小增量,减少预排序轮次,提升效率。 +1的保障作用:确保最后一次gap一定为 1(即最终进行直接插入排序),避免因整除导致gap跳过 1(如gap=2/3≈0会遗漏排序)
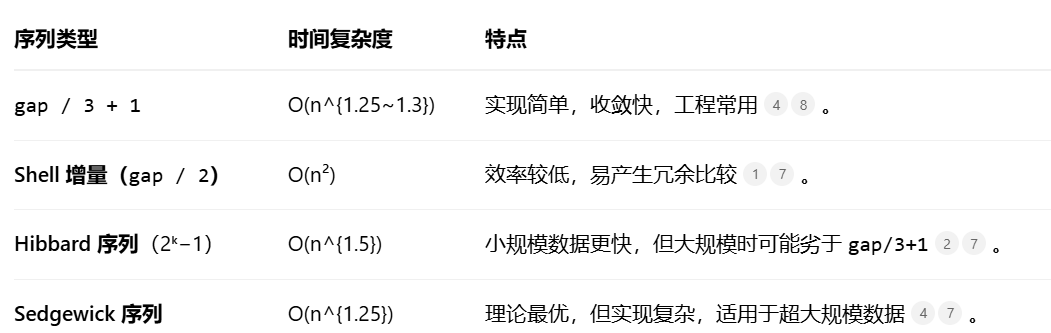
在gap选择3的时间复杂度
希尔排序的时间复杂度依赖gap序列,使用gap / 3 + 1时:- 平均时间复杂度:O(n^{1.25}) ~ O(n^{1.3})
通过预排序减少逆序对,最后一轮插入排序时数组已基本有序,移动次数接近线性。 - 最坏时间复杂度:O(n^{1.5})(若初始序列完全逆序)。
- 最优时间复杂度:O(n)(数组已有序时)
希尔排序以分组插入+增量缩减为核心,在插入排序基础上实现效率跃升,是算法优化的经典案例。其设计思想(分阶段逼近有序)深刻影响了后续算法(如快速排序分区策略)。尽管非稳定且理论分析复杂,其简洁性与实用效率仍使其成为工程排序的常用基础方案
1.2 堆排序:
堆排序是借助堆的特性来完成的,堆是一种特殊的二叉树,这种排序类似与选择排序很类似,都是把大的往后放,在建立堆,我们建立大堆,记得使用向下建堆方式(效率更高),从第一个非叶子节点开始建堆,建完堆后我们进行排序,把大的和最后一个进行交换,end-1,进行向下调整。这样还是第二大的就排序上去了,依次如此:
void AdJustDown(int* a, int size, int parent)
{//向下调整算法:int child = parent * 2 + 1;while (child < size){if (child + 1 < size && a[child] < a[child + 1]){child = child + 1;}if (a[child] > a[parent]){swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else {break;}}
}void HeapSort(int* a,int n)
{//排升序,我们建立大堆//向下建堆for (int i = (n - 1) / 2; i >= 0; i--){AdJustDown(a, n, i);}for (int i = 0; i < n; i++){swap(&a[0], &a[n - i - 1]);AdJustDown(a, n - i - 1,0);}
}
完成代码的构建,由于之前写过还是比较得心应手的。
1.3 测试:
两端测试:
void HeapTest()
{int arr[] = { 0, 14, 7,11,2,4,3,12,9 };HeapSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArr(arr, sizeof(arr) / sizeof(arr[0]));
}
void SelectTest()
{int arr[] = { 0, 14, 7,11,2,4,3,12,9 };SelectSort(arr, sizeof(arr) / sizeof(arr[0]));PrintArr(arr, sizeof(arr) / sizeof(arr[0]));
}
两次测试结果都很好。