[激光原理与应用-259]：理论 - 几何光学 - 平面镜的反射、平面透镜的折射、平面镜的反射成像、平面透镜的成像的规律

一、平面镜的反射规律

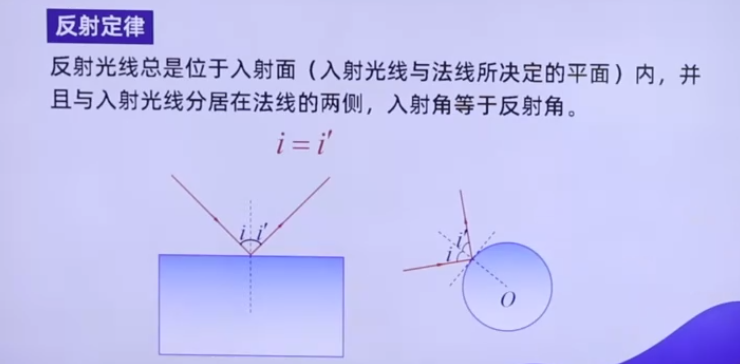
平面镜的反射遵循镜面反射定律，即光线在光滑表面（反射面平整度远大于波长）发生反射时，满足以下条件：

1. 反射光线、入射光线与法线共面：反射光线、入射光线和法线（垂直于反射面的直线）位于同一平面内。
2. 反射光线与入射光线分居法线两侧：反射光线和入射光线分别位于法线的两侧。
3. 反射角等于入射角：反射光线与法线的夹角（反射角）等于入射光线与法线的夹角（入射角），即 θr​=θi​。
4. 光路可逆性：若反射光线沿原入射方向射回，则光线将沿原入射光线方向返回。

二、平面透镜的折射规律

2.1 光的折射

平面透镜（如平行平板玻璃）的折射遵循斯涅尔定律（折射定律），即光线从一种介质进入另一种折射率不同的介质时，入射角与折射角的关系为：

n1​sinθ1​=n2​sinθ2​

其中：

• n1​ 和 n2​ 分别为两种介质的折射率（如空气 n1​≈1，玻璃 n2​≈1.5）。
• θ1​ 和 θ2​ 分别为入射角和折射角（以法线为基准）。

特殊情况：

• 当光线垂直入射（θ1​=0∘）时，折射角 θ2​=0∘，光线方向不变。
• 平行平板玻璃：光线通过上下表面各发生一次折射，出射光线与入射光线平行，但会发生侧向位移（位移量 d=t⋅cosrsin(i−r)​，其中 t 为平板厚度，i 为入射角，r 为折射角）。

2.2 光的色散

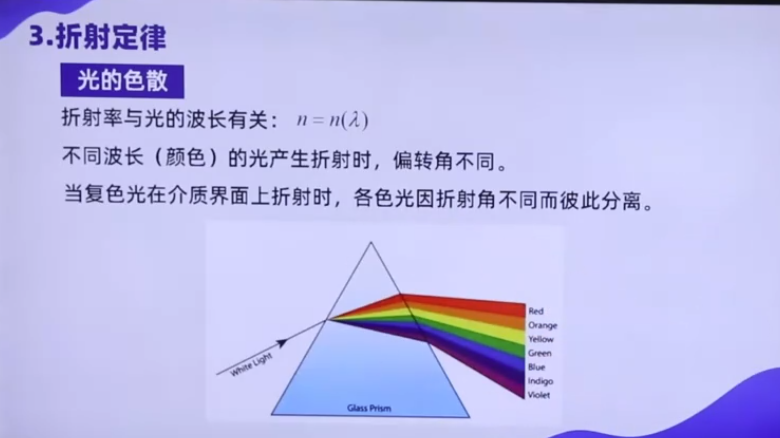
光的色散是光通过介质时，因不同波长（颜色）的光折射率不同，导致光线分离成彩色光谱的现象。这一现象揭示了光的复合性与波动性，是光学领域的重要基础。

1、色散的成因

光由不同波长的电磁波组成，当它从一种介质进入另一种介质（如从空气进入玻璃）时，各波长光的传播速度变化不同，导致折射角差异。根据斯涅尔定律 n1​sinθ1​=n2​sinθ2​，折射率 n 随波长 λ 变化（n 与 λ 成反比），因此短波长（如蓝光）折射角更大，长波长（如红光）折射角更小，最终光线分散为连续光谱。

2、自然与实验中的色散

1. 彩虹：雨滴作为天然三棱镜，阳光进入水滴后发生折射、内部反射和再次折射，不同波长的光因色散分离，形成七色圆弧。
2. 三棱镜实验：白光通过三棱镜后，因各色光折射率不同，在屏上呈现从红到紫的彩色条带（牛顿首次通过此实验证明白光由复合色光组成）。
3. 光栅色散：利用光栅的周期性结构，通过衍射和干涉效应实现更精确的色散，广泛应用于光谱仪中分析物质成分。

3、色散的应用

1. 光谱分析：通过分解光波获取物质指纹信息，如天文学中通过恒星光谱判断元素组成，化学中通过发射/吸收光谱鉴定物质。
2. 光学仪器：显微镜、望远镜的透镜组需采用低色散材料（如萤石）或复合镜片（如消色差透镜），以减少色差，提高成像清晰度。
3. 光纤通信：利用色散管理技术（如非零色散位移光纤）控制光脉冲展宽，避免信号失真，提升传输容量。

4、色散的局限性

色散可能导致光能分散和信号畸变。例如，在成像系统中，色差会降低图像边缘的锐度；在高速通信中，过大的色散会限制传输距离。因此，需通过材料选择（如使用低色散玻璃）或光学设计（如添加色散补偿元件）加以抑制。

2.3 光的全反射

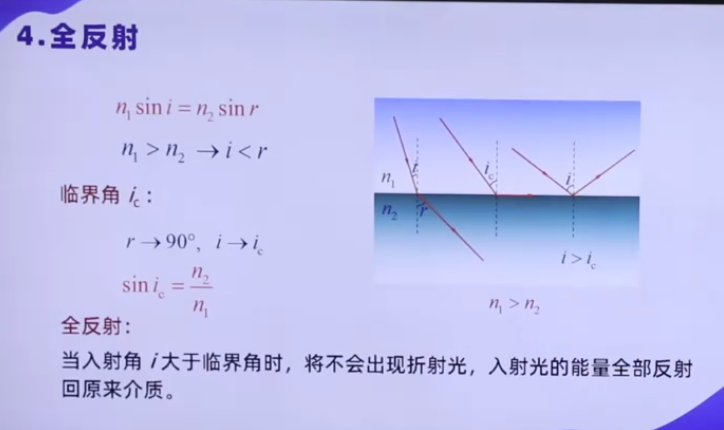
光的全反射是光从光密介质（折射率较高）进入光疏介质（折射率较低）时，当入射角增大到某一临界值后，光线不再发生折射，而是全部反射回原介质的现象。这一现象是光学中重要的物理过程，广泛应用于光纤通信、显微镜设计等领域。

1、全反射的临界条件

全反射的发生需满足两个条件：

1. 介质条件：光必须从折射率较大的介质（如玻璃 n1​≈1.5）射向折射率较小的介质（如空气 n2​≈1）。

2. 角度条件：入射角 θ1​ 需大于或等于临界角 θc​，临界角由斯涅尔定律推导得出：

θc​=arcsin(n1​n2​​).

例如，光从玻璃（n1​=1.5）射向空气（n2​=1）时，临界角约为 41.8∘。当入射角 θ1​≥41.8∘ 时，光线将发生全反射。

2、全反射的物理机制

当光从光密介质射向光疏介质时，折射光线逐渐远离法线。若入射角增大至临界角，折射角达到 90∘，此时折射光线沿界面传播，能量完全集中在反射光中。若入射角进一步增大，折射光线消失，所有能量被反射回原介质，形成全反射。

3、全反射的应用

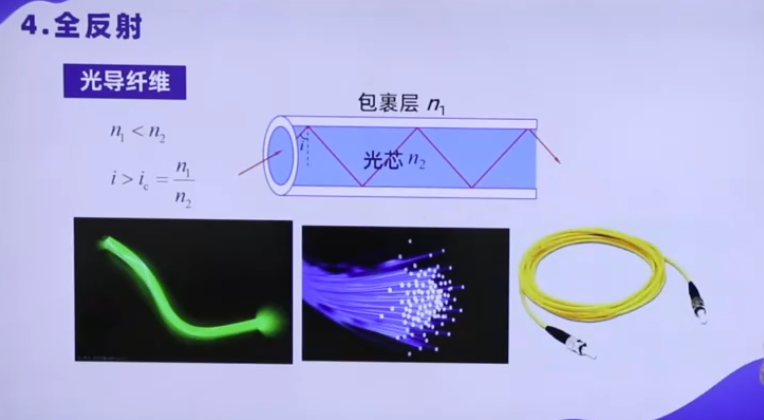
1. 光纤通信：光纤由高折射率纤芯和低折射率包层构成，光在纤芯中以全反射方式传播，实现低损耗、长距离信号传输。
2. 光学显微镜：全反射荧光显微镜利用全反射激发样品表面荧光，提高成像分辨率。
3. 棱镜设计：直角棱镜通过全反射改变光路，避免传统反射镜的能量损失。
4. 传感器：全反射式传感器通过检测反射光强度变化，测量液体折射率或表面位移。

4、全反射的局限性

全反射要求严格的光密-光疏介质界面，且入射角需精确控制。此外，界面粗糙度或杂质会导致散射，降低反射效率。在实际应用中，需通过镀增透膜、优化材料纯度等手段减少能量损失。

三、平面镜的成像规律

平面镜成像由反射光线反向延长线交汇形成，具有以下特性：

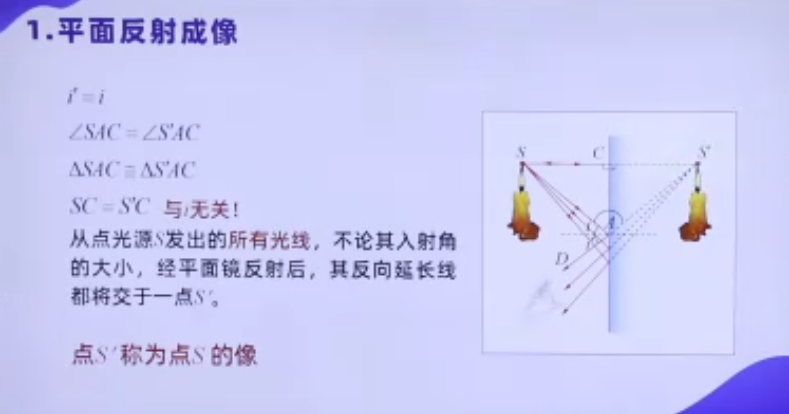
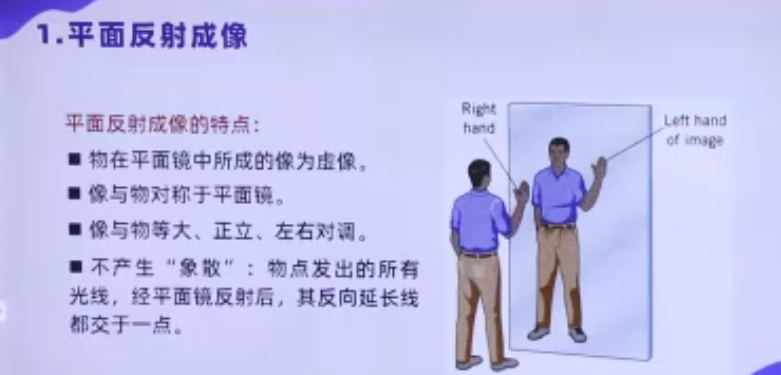
1. 虚像：像点由反射光线的反向延长线相交产生，无法在光屏上呈现（如镜子中的像）。
2. 等大：像与物体大小相等，视觉上的“近大远小”仅源于人眼视角变化。
3. 正立：像与物体方向一致（上下不颠倒，左右对调）。
4. 等距：像到镜面的距离等于物体到镜面的距离。
5. 对称性：像与物体的连线垂直于镜面，且关于镜面对称。

成像原理：

• 物体发出的光经镜面反射后，反射光线的反向延长线交汇形成虚像。
• 成像作图法：通过反射定律和对称性可确定像的位置和大小。

四、平面透镜成像

平面透镜（如平行平板玻璃）通常不改变光束的会聚或发散状态，看到的都是原先大小的实像。

只不过光学的强度被吸收，亮度会受损！

平面透镜（如平行平板玻璃）对光束传播特性的影响可从几何光学和能量传输两个层面进行深入分析，其核心结论可归纳如下：

1、几何光学：光束会聚/发散状态不变

1. 平行平板的等效折射
   当光束以任意角度入射平行平板（厚度为 d，折射率为 n）时，光线会发生两次折射：

   • 第一次折射（空气→玻璃）：入射角 θ1​，折射角 θ2​，满足斯涅尔定律 sinθ1​=nsinθ2​。
   • 第二次折射（玻璃→空气）：光线从平板另一侧射出时，折射角恢复为 θ1​，出射光线与入射光线平行（方向可能偏移）。

   关键结论：无论光束原本是会聚、发散还是平行，经过平行平板后，其会聚/发散状态（即光线的相对角度关系）保持不变，仅整体发生横向平移（位移量 Δx=d⋅sin(θ1​−θ2​)/cosθ2​）。

2. 成像特性

   • 实像位置不变：若原光束会聚于某点 P，经平板后仍会聚于 P，但光线路径因折射产生侧向位移。
   • 像的大小不变：由于光线角度关系未改变，横向放大率 M=1，因此成像大小与原物一致。
   • 无像差引入：平行平板为均匀介质，不引入球差、彗差等几何像差，成像质量仅受材料均匀性影响。

2、能量传输：亮度受损的物理机制

1. 吸收损耗
   玻璃材料对光存在吸收作用，其强度衰减遵循比尔-朗伯定律：

I=I0​e−αd,

其中 α 为吸收系数，d 为平板厚度。普通光学玻璃（如K9玻璃）在可见光波段的吸收系数极小（α≈10−3∼10−4cm−1），但厚平板仍可能导致可测量的亮度下降。

1. 表面反射损耗
   每次折射均伴随表面反射，反射率 R 由菲涅尔公式决定：

R=(n1​+n2​n1​−n2​​)2,

对于空气-玻璃界面（n1​=1, n2​=1.5），单面反射率 R≈4%。光线两次通过界面时，总反射损耗约为 8%（忽略多次反射）。
减反措施：镀增透膜（如MgF₂，n≈1.38）可将反射率降至 0.5% 以下。

1. 散射损耗
   材料内部杂质或表面粗糙度会导致光散射，使部分光线偏离原传播方向。高质量光学玻璃的散射损耗可忽略不计，但普通玻璃或塑料平板可能引入显著散射。

3、实际应用中的权衡

1. 光学仪器设计
   • 窗口片：在光谱仪、激光腔等系统中，平行平板作为保护窗口，需选择低吸收、低散射材料（如熔融石英），并镀增透膜以最大化透射率。
   • 光束位移器：利用平行平板的侧向位移特性，可调整光路布局而不改变光束聚焦状态。
2. 亮度优化策略
   • 材料选择：优先使用高透过率材料（如BK7玻璃，透过率 >92%/mm）。
   • 镀膜技术：在空气-玻璃界面镀单层或多层增透膜，将总透射率提升至 99% 以上。
   • 表面加工：通过超精密抛光（表面粗糙度 <λ/10）减少散射损耗。

总结

平行平板玻璃对光束的几何特性（会聚/发散状态、像大小）无影响，但会通过吸收、反射和散射降低光强。其核心优势在于保持光路方向性，而亮度损耗可通过材料优化和镀膜技术显著抑制。这一特性使其成为光学系统中调整光路、保护元件的理想选择。

五、平面折射成像与像散

像散是光学系统中一种典型的成像缺陷，其本质是同一物点发出的光线经过系统折射后，因方向依赖性折射差异，无法汇聚于单一像点，导致像的模糊与重叠。这一现象可拆解为以下关键环节：

1、光线分裂：子午与弧矢方向的“分道扬镳”

当光线通过非理想光学系统（如倾斜的透镜或曲面不对称的镜组）时，系统对不同方向的光线折射能力出现差异：

1. 子午光线（位于含光轴的截面内）与弧矢光线（垂直于光轴的截面内）因经过的曲面曲率不同，折射角度产生偏差。
2. 例如，一束平行光入射时，子午光线可能聚焦在像面前方，而弧矢光线聚焦在后方，形成两条分离的焦线（子午焦线与弧矢焦线）。
3. 同一物点发出的所有光线因此被“分裂”为两组，其延长线在像空间无法相交于一点，而是形成一条短线或椭圆光斑。

2、像的退化：从“点”到“弥散斑”的模糊

像散的直接后果是物点的像被“打散”：

1. 点扩散函数（PSF）变形：理想系统中，物点应形成对称的艾里斑；而存在像散时，PSF沿子午/弧矢方向延展为交叉的线状或椭圆，能量分散导致像的对比度下降。
2. 离轴像模糊加剧：像散强度通常随视场角增大而增强，导致图像边缘区域像质显著恶化（如广角镜头边缘的星点拖尾）。
3. 像重叠与混淆：不同物点的弥散斑部分重叠，使图像细节“发虚”（如显微镜中细胞结构的边界模糊）。

3、视觉表现：清晰像的“破碎感”

观察者会感知到：

1. 方向性模糊：像的模糊程度随方向变化，例如水平线条在垂直方向更模糊，反之亦然。
2. 局部清晰与整体模糊的矛盾：在子午或弧矢焦线附近，像可能短暂清晰，但其他方向仍模糊，形成“撕裂感”。
3. 动态场景中的拖影：在高速成像或振动环境中，像散会加剧运动物体的拖尾效应。

4、类比理解：光线的“路径分歧”

可将像散类比为：

• 多车道汇流：若不同方向的车流（光线）在交汇点（像点）因道路坡度（折射率）不同，导致车辆（光子）无法同时到达，形成拥堵（光斑）。
• 透镜的“偏食”：系统对特定方向的光线“偏爱”（折射更强），而对其他方向“忽视”，最终像的能量分布失衡。

5、总结：像散的“破坏性”与校正必要性

像散如同将清晰的像“撕成碎片”，其根源在于光学系统对光线方向的非均匀处理。这一现象在精密成像（如天文观测、半导体检测）中尤为致命，需通过对称设计、非球面校正或自适应光学等技术“重组”光线，恢复物点的锐利成像。理解像散，是掌握光学系统像差控制的关键一步。

六、平面折射近轴成像

平面折射近轴成像是几何光学中的重要概念，指光在两种介质分界面为平面的情况下，以近轴光线（与光轴夹角极小且靠近光轴的光线）成像的过程。以下从成像原理、特点、公式及应用等方面展开介绍：

1. 成像原理

当光线从一种介质进入另一种介质时，由于两种介质的折射率不同，光线会发生折射。在近轴条件下，即光线与光轴的夹角极小，可利用傍轴近似（如sinθ≈tanθ≈θ）简化计算。此时，从物点发出的近轴光线经平面折射后，虽然光线方向发生改变，但光束的同心性得以保持，从而形成清晰的像。

2. 成像特点

1. 无像差：在近轴近似下，高阶像差（如球差、彗差等）被忽略，成像为理想状态。
2. 物像共轭：物点与像点一一对应，满足特定的物像关系公式。
3. 线性关系：横向放大率恒定，像的几何形状与物严格相似。
4. 轴向位移：平行平板（如玻璃板）在近轴区成像时，仅引起光线的轴向位移（纵向平移），不改变光线的同心性或成像性质，因此在近轴区成完善像（无像差的清晰像）。

3. 成像公式

在近轴条件下，平面折射成像的物像位置关系可通过特定公式计算。对于给定的物点（物距L），其像位置（像距L′）与光线与折射平面法线的夹角U（或入射角I）有关。在近轴近似下，当光线接近垂直于折射平面时（即I=I′≈0），像散差为0，此时成像最为理想。对于平行平板玻璃，其近轴成像的轴向位移ΔL′可表示为：ΔL′=d(1−n1​)，其中d为平板厚度，n为平板材料的折射率。

4. 应用实例

1. 平行平板玻璃：如玻璃窗、保护玻璃等，在近轴条件下可近似成像，像可认为是由物体经过轴向位移得到。
2. 光学仪器：在设计光学仪器（如显微镜、望远镜等）时，近轴光学公式可用于近似确定像的位置和大小，为方案制定和原理分析提供依据。
3. 人眼成像：在眼视光学中，近轴成像原理有助于理解光线经眼球折射后如何在视网膜上形成清晰像。

七、什么是成像

成像是指光学系统或其他物理系统将物体发出的光线（或信号）经过传递、转换后，在特定位置形成与原物体相似或可解析的图形的过程。它是光学、摄影、显微技术、遥感等领域的核心概念，本质是信息的空间再分配。以下从原理、类型、应用及关键指标四方面展开说明：

1、成像的物理基础：光线的传递与聚焦

成像的核心是光线追踪，即通过几何光学或波动光学分析物体发出（或反射）的光线如何被系统处理：

1. 几何光学视角：
   • 物体可视为无数点光源的集合，每个点发出的光线经光学系统（如透镜、反射镜）折射或反射后，遵循直线传播规律。
   • 若系统能将同一物点发出的所有光线汇聚到像空间的一点（像点），则形成清晰像；否则像模糊。
   • 例子：凸透镜成像中，物距 u、像距 v 与焦距 f 满足 u1​+v1​=f1​，实现倒立实像或正立虚像。
2. 波动光学视角：
   • 光具有波粒二象性，成像需考虑衍射效应。即使系统几何完美，光波通过有限孔径时也会产生衍射极限（如艾里斑），限制分辨率。
   • 例子：显微镜的分辨率受波长 λ 和数值孔径 NA 限制，公式为 d=NA0.61λ​。

2、成像的类型：从理想到实际

根据系统特性与像质，成像可分为以下类型：

1. 理想成像：
   • 满足等光程条件（物点到像点的光程相等），像与物严格相似（大小、方向可能变化）。
   • 例子：平面镜成像（虚像）、薄透镜中心区域成像。
2. 实际成像：
   • 受像差（如球差、色差、像散）影响，像发生变形或模糊。
   • 例子：
     • 球差：透镜边缘光线聚焦于不同位置，导致像点周围出现光晕；
     • 色差：不同波长光折射率不同，像边缘出现彩色镶边；
     • 像散（如前文所述）：子午与弧矢方向光线无法汇聚，像呈十字形模糊。
3. 计算成像：
   • 通过算法补偿系统缺陷或突破物理限制，如压缩感知、去卷积、相位恢复等。
   • 例子：手机相机通过多帧合成校正手抖模糊；天文望远镜用自适应光学抵消大气湍流。

3、成像的应用：从微观到宏观

成像技术贯穿人类探索世界的各个尺度：

1. 微观成像：
   • 光学显微镜：利用可见光观察细胞、微生物（分辨率约200nm）；
   • 电子显微镜：用电子束替代光束，实现原子级分辨率（如扫描隧道显微镜，STM）。
2. 宏观成像：
   • 摄影与摄像：记录可见光场景，艺术与科学记录工具；
   • 遥感成像：通过卫星或飞机搭载传感器，获取地表信息（如多光谱成像监测植被健康）。
3. 特殊波段成像：
   • X射线成像：医学CT扫描，观察人体内部结构；
   • 红外成像：夜间监控或热成像，检测物体温度分布；
   • 超声波成像：医学B超，利用声波反射生成组织图像。

4、成像质量的关键指标

评价成像系统性能的核心参数包括：

1. 分辨率：系统能分辨的最小细节尺寸（如显微镜的瑞利判据）；
2. 对比度：像中明暗区域的亮度差异，反映细节可见性；
3. 畸变：像的几何变形程度（如桶形畸变、枕形畸变）；
4. 信噪比（SNR）：有效信号与背景噪声的比值，影响图像清晰度；
5. 景深：系统能同时清晰成像的物空间深度范围。

5、总结：成像——连接物理与信息的桥梁

成像不仅是“光的汇聚”，更是物体信息通过物理系统的编码与解码过程。

从古代小孔成像到现代量子成像，其发展始终围绕两个核心目标：

1. 提高保真度：减少像差与噪声，逼近理想成像；
2. 拓展能力边界：突破分辨率、波段、速度等物理限制（如超分辨显微技术）。

理解成像的本质，有助于我们设计更精密的光学系统，或开发创新的计算方法，最终揭示自然界的隐藏细节——无论是纳米级的细胞结构，还是光年外的星系演化。