B系列树详细讲解

在这篇文章中我们围绕着B树、B+树和B*树进行详细讲解

一.B树

引言：在面对数据量不是很大时，可以直接拷到内存中使用，但是当面对磁盘中数据量非常大时，无法一次拷贝到内存中，那么如果需要进行搜索等相关操作，该如何解决呢？

此时可以想到：存放关键字和其在磁盘隐射的地址在内存中，如果查找发现需要该详细数据，就去对应的磁盘中查看，减少磁盘I/O次数，提高效率，这就是B树

B树概念：

一棵m（m >= 2）阶树，是一个M路平衡搜索树，该树可以为空，如果不为空，有以下性质：

1.根至少有两个孩子

2.每个分支节点都包含k-1个关键字和k个孩子（孩子存放的是隐射地址），关键词存放的是key，k的取值范围为（m/2）向上取整<= k <= m

3.对于每个叶子节点，同样是k-1个关键字和k个孩子，但是B树需要保证叶子节点都在同一层上

4.每个节点的关键字都需要从小到大排好序，k-1个关键字正好可以划分k个孩子，如下图：

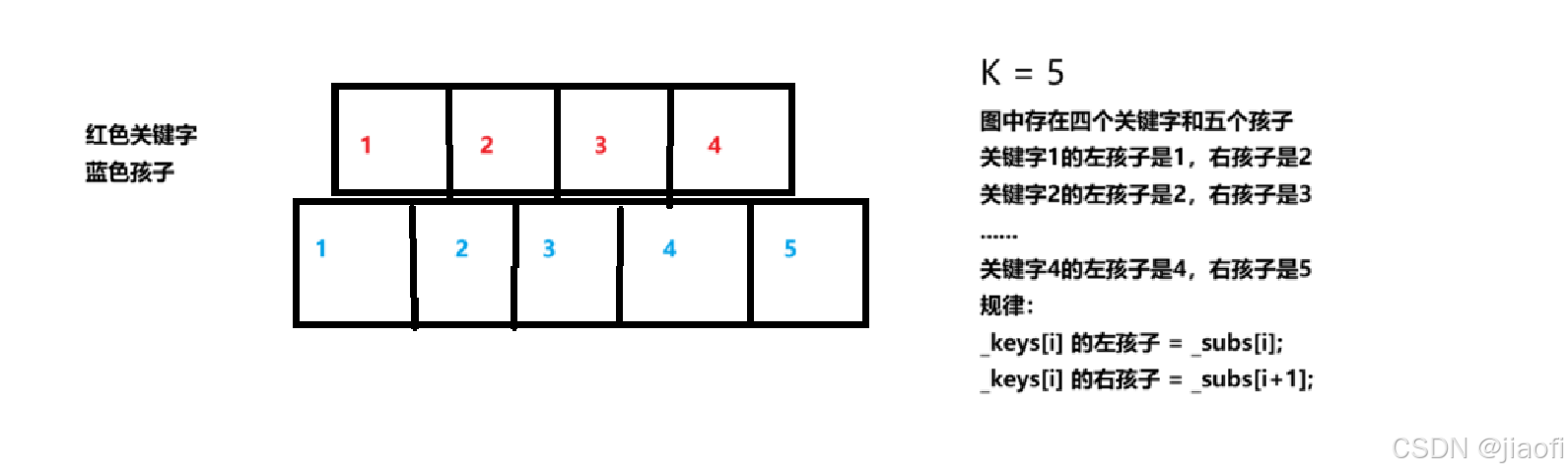
下面我们讲解下插入的主要思路：

在节点上插入，存放在关键字中，当该节点满了，接下来找到中位数，将中位数右边的值存放在新开辟的兄弟节点中，中位数存放在父节点中，如果不存在父节点，就新建，如果存放后父节点也满了，重复上述操作，不要忘记将节点关键字对应的孩子也要分裂，补充说明：我们实现的插入一定是在叶子节点上插入的，因此B数是向上向右扩展的

B树的删除原理;

通过查找来删除数据，当找到时，我们不能直接删除，需要观察删除后的影响，如果删除后该节点中关键字< (k/2)-1,需要去向父节点中借关键字，如果父亲无法借，接下来去兄弟借，如果还不行，再向父亲的兄弟借，依次向上借节点，知道满足，才能保证叶子节点在同一层，当然实际还不止这么简单，还需要适当的合并，总而言之，删除更加复杂，如果你感兴趣可以去《算法导论》中或者

《数据结构-殷人昆》中学习，后面我们不实现删除的

接下来我们来实现对于B数的插入和查找代码实现：

注意的是在实际中我们存放k个关键字和k+1个孩子,方便后续分裂新节点，具体代码如下：

#include <iostream> using namespace std;//B树实现：
//Node:
template<class K,size_t M>
struct BTreeNode
{//正常情况下我们是定义M-1个关键字，M个孩子，但是为了方便分裂，我们是M个关键字，M+1个孩子K _keys[M];//每个节点的关键字数量BTreeNode<K,M>* _subs[M+1];//M+1个孩子 ，存放的是指针BTreeNode<K,M>* _parent;//父结点size_t n;//实际上使用的关键之数量 BTreeNode(){//将关键之和孩子全部初始化默认值for(size_t i = 0;i < M;++i) {_keys[i] = K();_subs[i] = nullptr;}//孩子多一个_subs[M] = nullptr;//初始化父结点和实际关键字数量 _parent = nullptr;_n = 0;		}
}; 
//Tree
template<class K,size_t M>
class BTree
{typedef BTreeNode<K,M> Node;
public://查找pair<Node*,int> Find(const K& key) {Node* parent = nullptr;Node* cur = _root;while(cur){size_t i = 0;while(i < cur->_n){//在当前节点中查找关键字if(key < cur->_keys[i]){//说明在其孩子存放的下一级中break; } else if(key > cur->_keys[i]){//还可能在其右边关键字中i++; }else{//找到了return make_pair(cur,i);//返回当前节点和在其中关键字位置 }}//跳到孩子上parent = cur;cur = cur->_subs[i];//注意i对应的就是比当前节点小的孩子上 }//找到最后都没有找到，返回需要构造的父结点，其子节点可以存放该keyreturn make_pair(parent,-1);}//直接使用默认构造，不s实现bool Insert(const K& key) {if(root == nullptr){//初始插入_root = new Node;_root -> _keys[0] = key;_root -> _n ++;return true; }//非初始化插入//B树具有每个关键字都不相同特性，相同不允许插入//利用Find查找pair<Node*,int> res = Find(key);if(res.second != -1){//已存在，不允许插入return false; }//不存在，插入,插入的位置由parent标出Node* parent = res.first;K newkey = key;Node* child = nullptr; while(1){//先插入，后续在检查是否满了InsertKey(parent,newkey,child);//判断是否满了if(parent->_n < M)//等于M时就是利用了我们的多开的空间 {return true;}else{//分裂size_t mid = M / 2;Node* brother = new Node;int left = 0;//分裂左边[0,mid) int right = mid + 1;//分裂右边[right,M)int tmp = 0;//计数 while(right < M) {//分裂拷贝brother->_keys[tmp] = parent->_keys[right];brother->_subs[tmp] = parent->_subs[right];if(parent->_subs[right]){//该parent不是叶子节点，_subs[i]存在下一级//所以要将孩子的父指针也继承给兄弟parent->_subs[right]->_parent = brother; }tmp++;//拷贝走的内容置空parent->_keys[right] = K();parent->_subs[right] = nullptr;	right++; }//由于孩子比关键字多一个，格外处理brother->_subs[tmp] = parent->_subs[right];//也需要判断是否需要继承下一代if(parent->_subs[right]) {parent->_subs[right]->_parent = brother;}parent->_subs[right] = nullptr;//处理//处理中位数和_nbrother->_n = tmp;parent->_n -= (tmp + 1);K midkey = parent->_keys[mid];parent->_keys[mid] = K();//如果刚刚分裂的是根节点if(parent->_parent == nullptr) {_root = new Node;_root->_keys[0] = midkey;_root->_subs[0] = parent;_root->_subs[1] = brother;_root->_n = 1;parent->_parent = _root;brother->_parent = _root;break;}else{//非根节点//重新走循环newkey = midkey;child = brother;parent = parent->_parent; }}}}//方便查看:中序:左-根-右 void InOrder(){_InOrder(_root);}
private:void _InOrder(Node* cur){if (cur == nullptr)return;// 左 根  左 根  ...  右size_t i = 0;for (; i < cur->_n; ++i){_InOrder(cur->_subs[i]); // 左子树cout << cur->_keys[i] << " "; // 根}_InOrder(cur->_subs[i]); // 最后的那个右子树}void InsertKey(Node* node, const K& key, Node* child){int end = node->_n - 1;while(end >= 0){if(key < node->_keys[end){//后移原位置node->_keys[end + 1]  = node->_keys[end];//不要忘了孩子node->_subs[end + 2] = node->_subs[end + 1];end--;}else{//找到要插入的位置了 break;}					}node->_keys[end + 1] = key;node->_subs[end + 2] = child;if(child){//孩子存在，孩子的父指针也要得到相应设置child->_parent = node; }_node -> _n ++;}//成员变量: Node* root = nullptr;//根节点	
};int main()
{return 0;
}

现在B数相关的部分大体我们了解了，请回答下面这个简单问题：

为什么在磁盘等外存中不适合使用哈希或者AVL树，亦或者红黑树？？？

平衡搜索树高度是LogN，看起来不大，但是磁盘I/O是非常消耗时间的，所以不能再外存中使用；哈希面对数据量非常的的情况下哈希冲突也是严重，导致访问次数剧增，B树实际是M=1024的情况下，我们只需要四层就可以存放1024*1024*1024*1023个关键字，约1000亿个数据，此时就可以快速到磁盘中定位，减少I/O次数，效率高

二.B+树

B+树是B树的变形，基于B树优化的多路平衡搜索树，在MySQL的搜素引擎Innodb和MyIsam中就有使用，下面来讲解下其特性:

1.分支节点的关键字和孩子数量一样多，如下图:

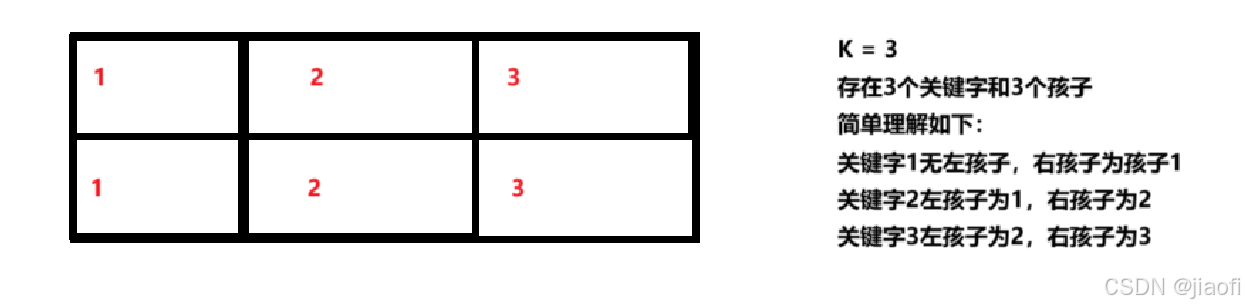
2.分支节点的子树指针p[i]指向关键字大小在[k[i],k[i+1])之间

3.将叶子节点通过一个链表指针连接

4.分支节点和叶子节点存在重复值（B树是不存在的），分支节点记录的是叶子节点的索引

5.通常情况下分支节点是利用叶子节点的最小值做索引存放在关键字中

如下图：

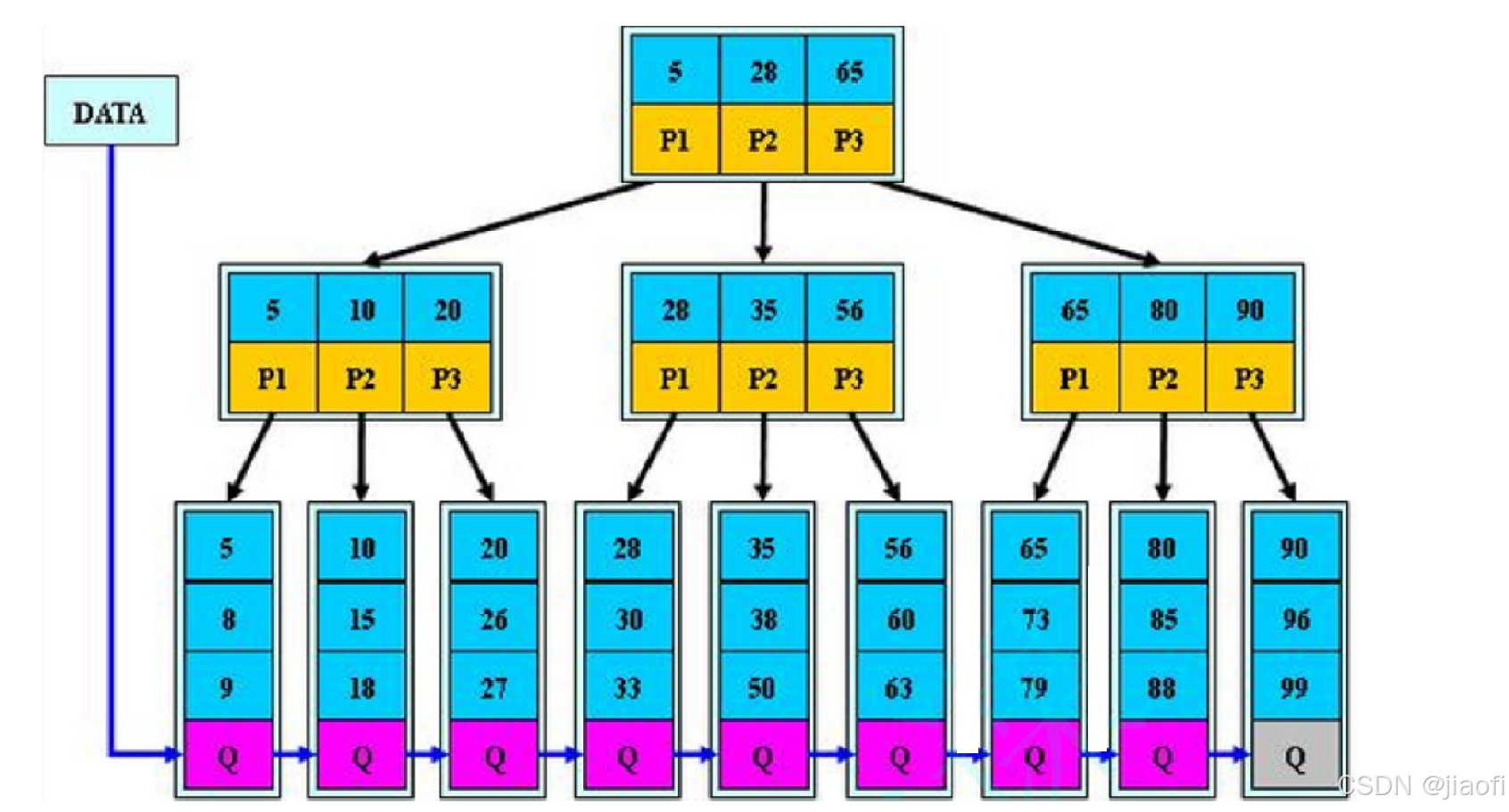
重点：B+树中一定要记住数据实际是存放在叶子中的，分支节点存放的是索引！！！

下面我们来模拟下B+树的分裂过程：

开始时就是直接建立两层，叶子层和根层，后续和B树一样，向叶子中插入，当叶子满了，就分裂给兄弟，分一半给兄弟，没有中位数向上，而是将兄弟最小值作为索引放在父节点中

接下来操作和B树一样

三.B*树

B*树是在B+树的基础上再一次变形，在B+树的非根节点和非叶子节点上引入指向兄弟的指针，如下图：

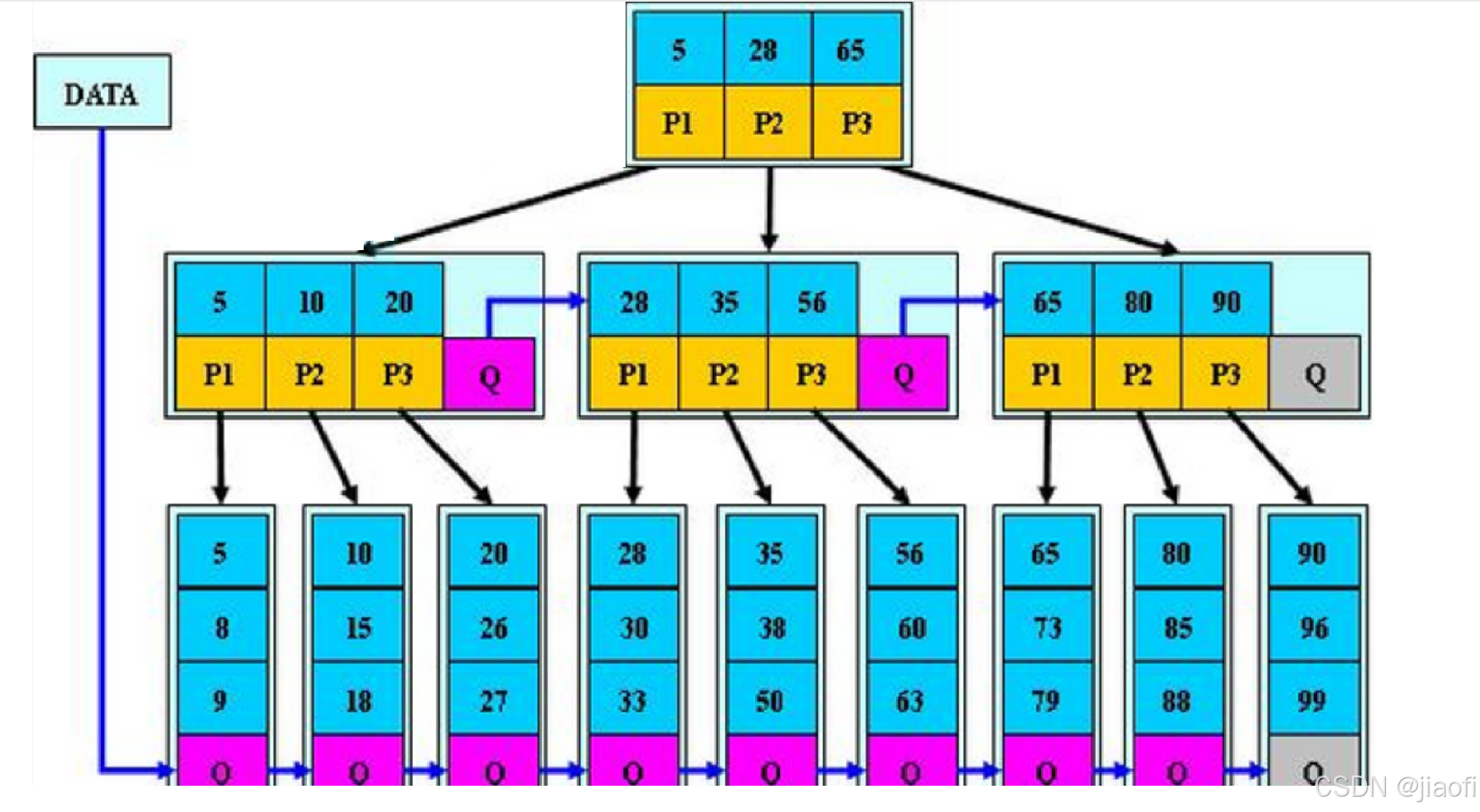
B*树分裂和B+树不同，B+树分裂影响的是当前节点和父节点，但是B*树不同，由于存在指向兄弟的指针，所以当当前节点满的时候，如果其兄弟节点未满，就会将数据分一部分到其兄弟上，然后再修改兄弟在父节点中的关键字（最小值改变）;当该节点和兄弟节点都满的时候，此时通过将该节点的后1/3和兄弟节点的前1/3分到新开辟的节点中，兄弟节点数据调整和修改兄弟节点在父节点的索引，在将新分配的节点索引存放在父节点中，其余同B树操作，判断是否继续分裂

这也可以看出B*树的作用：由于B树和B+树都可能存在空间利用率低的情况，引入B*树先向兄弟中存放，不能做到满足在开辟新节点，这样就大大提高空间利用率，但是实际使用并不多，原因是因为磁盘太大了，完全不用担心空间利用问题，毕竟B*树效率比不是比B+树好的，而且实现复杂

总结:

B树：有序数组+平衡多叉树

B+树：有序数组链表+平衡多叉树

B*树：实际上是一个更加丰满的B+树，空间利用率更高

感谢你的支持，后续我会讲解其在数据库中应用，欢迎查看！！！