算法详细讲解 - 离散化/区间合并
离散化
讲解
这里的离散化特指整数有序离散化。整个值域跨度很大,但是值非常稀疏的情况。
问题背景
我们有一个无限长的数轴,初始时每个位置上的值都是0。我们需要进行两种操作:
- 修改操作:在某个位置
x上增加一个值c。 - 查询操作:询问区间
[l, r]内所有位置的值之和。
数据范围
- 操作次数
n和查询次数m最多为10^5。 - 坐标
x和区间端点l,r的范围是-10^9到10^9。 - 修改值
c的范围是-10000到10000。
解题思路
由于坐标范围非常大(-10^9 到 10^9),直接使用数组存储每个位置的值会非常浪费空间。因此,我们需要使用离散化技术,将实际的坐标映射到一个小范围内。
离散化步骤
- 收集所有需要离散化的值:包括所有的修改位置
x和查询区间的端点l和r。 - 排序并去重:对这些值进行排序,并去掉重复的值。
- 映射:将每个原始值映射到一个新的小范围内的索引。
模板题
802. 区间和 - AcWing题库
#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;
const int N = 300010;
int n, m;
int a[N], s[N]; // 存数数组与前缀和数组
vector<int> alls; // 存储所有要离散化的值
vector<PII> add, query; // 添加与查询// 二分查找找到 x 在 alls 中的位置
int find(int x) {int l = 0, r = alls.size() - 1;while (l < r) {int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1; // 返回 x 映射后的位置
}int main() {cin >> n >> m;for (int i = 0; i < n; i++) {int x, c;cin >> x >> c;add.push_back({x, c});alls.push_back(x); // 收集需要离散化的值}for (int i = 0; i < m; i++) {int l, r;cin >> l >> r;query.push_back({l, r});alls.push_back(l);alls.push_back(r); // 收集需要离散化的值}// 对 alls 排序并去重sort(alls.begin(), alls.end());alls.erase(unique(alls.begin(), alls.end()), alls.end());// 处理插入操作for (auto item : add) {int x = find(item.first); // 找到 x 映射后的位置a[x] += item.second; // 在该位置增加 c}// 预处理前缀和for (int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + a[i];// 处理查询操作for (auto item : query) {int l = find(item.first), r = find(item.second); // 找到 l 和 r 映射后的位置cout << s[r] - s[l - 1] << endl; // 输出区间 [l, r] 的和}return 0;
}模板题讲解
pair 是为了 把“有关系的两个数据”绑在一起,方便一起存储和使用。
在本题中:
add操作需要两个数:位置x和 要加的值cquery查询也需要两个数:左端点l和 右端点r
我们用 pair<int, int> 把它们“配对”起来,这样就不会搞混。
想象你在记账:
| 时间 | 事件 |
|---|---|
| 3点 | 在超市花 50 元 |
| 5点 | 在餐厅花 100 元 |
你想记录这些操作,你会怎么存?错误方式:
vector<int> times = {3, 5};
vector<int> money = {50, 100};问题:如果排序或删除,很容易“时间”和“金额”对不上!
vector<pair<int, int>> records = {{3, 50}, {5, 100}};这样,3点 和 50元 永远是一对,不会错乱。
再回到题目:vector<PII> add; —— 存修改操作
for (int i = 0; i < n; i++) {int x, c;cin >> x >> c;add.push_back({x, c}); // 把“位置x”和“加的值c”绑在一起
}比如输入:
1 2
3 6
7 5add 变成:
add = { {1,2}, {3,6}, {7,5} }{1,2}表示:在位置 1 加 2{3,6}表示:在位置 3 加 6
好处:后面遍历的时候,item.first 就是 x,item.second 就是 c。
find函数的作用是什么?
int find(int x) {int l = 0, r = alls.size() - 1; // l=左边界,r=右边界while (l < r) { // 二分查找开始int mid = l + r >> 1; // 相当于 (l + r) / 2,找中间位置if (alls[mid] >= x) // 如果中间的数 >= xr = mid; // 说明 x 在左边,把右边界缩小到 midelse // 如果中间的数 < xl = mid + 1; // 说明 x 在右边,把左边界移到 mid+1}return r + 1; // 返回位置(+1 是因为窗口号从 1 开始,且r是下标,从0开始)
}这个 find 函数,就是在一个排好序的列表里,快速找到某个数 x 的“排名”(位置),然后返回它的“新编号”。find(x) 就像查字典:给你一个词(x),快速找到它在词典(alls)里的页码(新编号),方便后面查数据。
举个生活例子:排队领号
想象你去银行办事:
- 银行有 10 个窗口,但今天只有 3 个人来办业务,他们的号码是:
1, 3, 7 - 银行不想浪费窗口资源,于是说:“我们重新分配窗口号!”
- 把这三个号码 从小到大排序,然后按顺序分配新窗口号:
1→ 窗口 13→ 窗口 27→ 窗口 3
这个过程就叫 离散化:把很大的原始号码(比如 1亿),映射到很小的窗口号(1,2,3)。
在你的代码里,alls 就是那个“排好序的号码列表”。比如:
alls = {1, 3, 7} // 原始坐标,已经排序去重我们想问:
“原始坐标
3对应哪个窗口号?”
答案是:第 2 个位置 → 所以返回 2
| 原始坐标 x | 在 alls 中的下标 | 返回值(r+1) | 新编号 |
|---|---|---|---|
| 1 | 0 | 0+1 = 1 | 1 |
| 3 | 1 | 1+1 = 2 | 2 |
| 7 | 2 | 2+1 = 3 | 3 |
为什么用二分?不用直接找?
因为 alls 可能有 30 万个数,如果一个一个找(线性查找),太慢了!
- 线性查找:最多要查 30 万次
- 二分查找:最多查
log₂(30万) ≈ 19次
快了上万倍!
处理修改与查询操作
第一部分:处理修改操作
for (int i = 0; i < n; i++) {int x, c;cin >> x >> c; // 读入位置 x 和要加的值 cadd.push_back({x, c}); // 把 (x, c) 存起来,后面要用alls.push_back(x); // 把 x 记录下来,准备离散化!
}| i | x | c | add 变成 | alls 变成 |
|---|---|---|---|---|
| 0 | 1 | 2 | {1,2} | {1} |
| 1 | 3 | 6 | {1,2},{3,6} | {1,3} |
| 2 | 7 | 5 | {1,2},{3,6},{7,5} | {1,3,7} |
所以现在:
add存了所有“在哪加、加多少”alls存了所有被修改过的位置:1, 3, 7
第二部分:处理查询操作
for (int i = 0; i < m; i++) {int l, r;cin >> l >> r; // 读入查询区间 [l, r]query.push_back({l, r}); // 把 (l, r) 存起来,后面要用alls.push_back(l); // 把 l 记下来,也要离散化!alls.push_back(r); // 把 r 记下来,也要离散化!
}| i | l | r | query 变成 | alls 新增 |
|---|---|---|---|---|
| 0 | 1 | 3 | {1,3} | 1, 3 → alls = {1,3,7,1,3} |
| 1 | 4 | 6 | {1,3},{4,6} | 4,6 → alls = {1,3,7,1,3,4,6} |
| 2 | 7 | 8 | {1,3},{4,6},{7,8} | 7,8 → alls = {1,3,7,1,3,4,6,7,8} |
为什么查询的 l 和 r 也要放进 alls?
因为我们要对所有出现过的坐标进行离散化!
你想啊,后面要查 [4,6] 的和,但 4 和 6 这两个位置根本没人改过,它们不在 add 里。
但我们必须知道:
4在离散化后对应哪个编号?6在离散化后对应哪个编号?
否则没法查区间!
所以:只要是出现过的坐标(无论是修改还是查询),都要放进 alls!
后面代码会做两件事:
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());排序 + 去重后变成:
{1, 3, 4, 6, 7, 8}然后我们就可以离散化了:
| 原始坐标 | 新编号(find 返回) |
|---|---|
| 1 | 1 |
| 3 | 2 |
| 4 | 3 |
| 6 | 4 |
| 7 | 5 |
| 8 | 6 |
处理插入,预处理前缀和,处理询问(输出每个区间的和)
第一段:处理插入(把值加到离散化后的位置)
for (auto item : add) {int x = find(item.first); // 找到原始位置对应的新编号a[x] += item.second; // 把值加到新位置上
}第一次:item = {1,2}
item.first = 1→find(1) = 1→x = 1a[1] += 2→a[1] = 2
第二次:item = {3,6}
find(3) = 2→x = 2a[2] += 6→a[2] = 6
第三次:item = {7,5}
find(7) = 5→x = 5a[5] += 5→a[5] = 5
现在 a 数组长这样(只看 1~6):
| 新编号 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 值 a[i] | 2 | 6 | 0 | 0 | 5 | 0 |
注意:a[i] 存的是离散化后编号为 i 的位置上的值
第二段:预处理前缀和
for (int i = 1; i <= alls.size(); i++)s[i] = s[i - 1] + a[i];alls.size() = 6,所以 i 从 1 到 6
我们来算 s[i],它表示:前 i 个离散化位置的值的总和
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| s[i] | 0 | 2 | 8 | 8 | 8 | 13 | 13 |
第三段:处理询问(输出每个区间的和)
for (auto item : query) {int l = find(item.first), r = find(item.second);cout << s[r] - s[l - 1] << endl;
}举个例子
查询 1:item = {1,3} → 查 [1,3] 的和
l = find(1) = 1r = find(3) = 2- 输出:
s[2] - s[1 - 1] = s[2] - s[0] = 8 - 0 = 8
区间合并
讲解
区间合并就是对区间求并集。
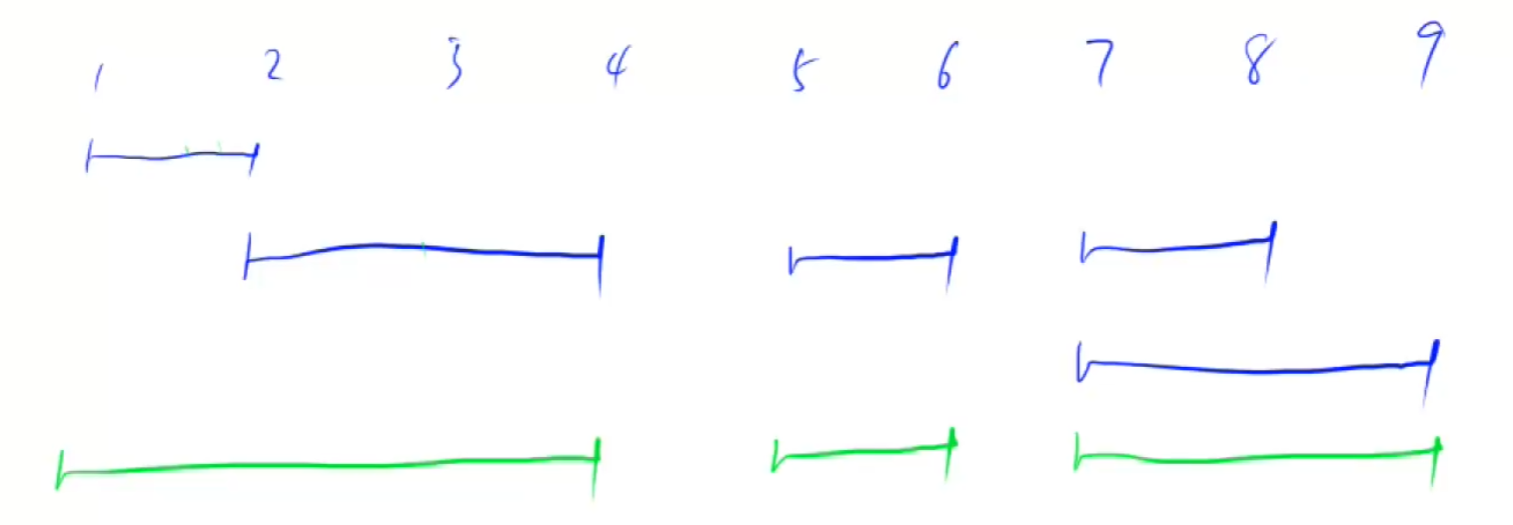
给定一些区间,比如 [1,3] 和 [2,6],如果这些区间有交集(包括端点相交),我们就需要把它们合并成一个更大的区间。最终我们要计算合并后剩下多少个不重叠的区间。
我们可以看到:
[1, 2]和[2, 4]有交集,可以合并成[1, 4][7, 8]和[7, 9]有交集,可以合并成[7, 9][5, 6]没有和其他区间交集,保持不变
所以最终合并后的区间是:
[1, 4][5, 6][7, 9]
因此,合并后的区间个数是 3。
模板题
AcWing 803. 区间合并 - AcWing
#include <bits/stdc++.h>
using namespace std;typedef pair<int, int> PII;// 合并区间的函数
void merge(vector<PII> &segs) {// 结果数组,存储合并后的区间vector<PII> res;// 对输入的区间按照起始位置进行排序sort(segs.begin(), segs.end());// 初始化当前区间的起始和结束位置int st = -2e9, ed = -2e9;// 遍历所有区间for (auto seg : segs) {// 如果当前区间的起始位置大于上一个区间的结束位置if (ed < seg.first) {// 如果st不是初始值,说明之前已经有一个区间了,将其加入结果数组if (st != -2e9) {res.push_back({st, ed});}// 更新当前区间的起始和结束位置st = seg.first, ed = seg.second;} else {// 如果当前区间的起始位置小于等于上一个区间的结束位置,说明有交集// 更新当前区间的结束位置为两者中的较大值ed = max(ed, seg.second);}}// 最后检查是否有剩余的区间未加入结果数组if (st != -2e9) {res.push_back({st, ed});}// 将结果数组赋值给原数组,完成合并操作segs = res;
}int main() {// 区间数量int n;cin >> n;// 创建一个vector来存储所有的区间vector<PII> segs;// 读取每个区间并存入vector中for (int i = 0; i < n; i++) {int l, r;cin >> l >> r;segs.push_back({l, r});}// 调用merge函数进行区间合并merge(segs);// 输出合并后的区间个数cout << segs.size() << endl;return 0;
}模板题讲解
int st = -2e9, ed = -2e9; 这一步是怎么来的?
目的是初始化一个“虚拟”的起始区间,用来方便地处理第一个真实区间的合并逻辑。
注意:-2e9 就是 -2 * 10^9,题目说区间范围是 -10^9 ≤ li ≤ ri ≤ 10^9,所以 -2e9 比所有可能的左端点都小,可以当作“负无穷”。
int st = -2e9, ed = -2e9; // 初始状态:没有正在合并的区间
for (auto seg : segs) {if (ed < seg.first) { // 当前区间无法和 seg 合并(断开了)if (st != -2e9) { // 如果 st 不是初始值,说明我们之前已经在合并某个真实区间res.push_back({st, ed}); // 把之前合并好的区间存进去}// 开启一个新的合并区间:就是当前这个 segst = seg.first;ed = seg.second;} else {// 能合并!更新当前合并区间的右边界ed = max(ed, seg.second);}
}
// 循环结束后,最后一个正在合并的区间还没加入结果
if (st != -2e9) {res.push_back({st, ed});
}为什么需要这个“虚拟起点”?
是为了统一处理逻辑,避免写一堆 if (第一个区间) 的判断。
比如如果没有这个技巧,你可能会写:
if (res.empty()) {st = seg.first;ed = seg.second;
} else if (ed < seg.first) {res.push_back({st, ed});st = seg.first;ed = seg.second;
} else {ed = max(ed, seg.second);
}int st = -2e9, ed = -2e9; 是一种编程技巧,叫做“哨兵”或“虚拟初始值”,作用是:
- 让你在处理第一个真实区间时,也能套用统一的逻辑;
- 用
st != -2e9来判断“是否已经开始合并一个真实区间”; - 避免特判第一个元素,让代码更简洁、不易出错。
