神经网络训练核心组件

一、梯度下降的优化算法

我们在机器学习的时候学习了三种传统的梯度下降算法，分别是批量梯度下降（BGD）、随机梯度下降（SGD）、小批量梯度下降（MGBD），但这些算法都存在一些问题。

• 收敛速度慢：BGD和MBGD使用固定学习率，太大会导致震荡，太小又收敛缓慢。

• 局部最小值和鞍点问题：SGD在遇到局部最小值或鞍点时容易停滞，导致模型难以达到全局最优。

• 训练不稳定：SGD中的噪声容易导致训练过程中不稳定，使得训练陷入震荡或不收敛。

接下来将介绍几种优化算法。

在这之前我们要了解一个概念——指数加权平均

指数加权平均：Exponential Moving Average，简称EMA，是一种平滑时间序列数据的技术，它通过对过去的值赋予不同的权重来计算平均值。

对序列 $x_t$，其指数加权平均 $s_t$ 定义为：

$s_t=\alpha \cdot x_{t-1}+(1-\alpha )\cdot s_t$

• $s_t$ 是时刻 $t$ 的 EMA
• $α∈(0,1) $是平滑因子（衰减率），$$\alpha$$ 越接近 $$1$$，表示对历史数据依赖性越高；越接近 $$0$$ 则越依赖当前数据。
• $x_t$ 是当前时刻的观测值
• 初始值 $s_0$ 通常设为 $x_0$ 或 0

Momentum优化法

动量（Momentum）是梯度下降优化方法的一种，可以更好地应对梯度变化和梯度消失问题，从而提高训练模型的效率和稳定性。该方法运用 指数加权平均 来积累历史梯度信息，从而在更新参数时形成“动量”，帮助优化算法更快地越过局部最优或鞍点。

算法过程：

1.更新动量项

$$v_t=\beta v_{t-1}+(1-\beta ){\nabla }_{\theta }J({\theta }_t)$$

其中：

• $$v_{t-1}$$ 是之前的动量项；
• $$\beta$$ 是动量系数（通常为 0.9）；
• $${\nabla }_{\theta }J({\theta }_t)$$ 是当前的梯度；

2.更新参数

用动量项更新参数：${\theta }_t={\theta }_{t-1}-\eta v_t$

特点：

• 由于利用了历史梯度，使得该方法具有“惯性”，会沿着当前方向继续更新参数，不会因为当前梯度逼近0而停滞。
• 该方法平滑了梯度更新，减少了鞍点附近的震荡，帮助优化过程稳定向前推进。
• 该方法在优化过程中持续沿着某个方向前进，能够更快地穿越鞍点区域，避免在鞍点附近长时间停留。

小结：

Momentum 算法是对梯度值的平滑调整，使得参数能够继续更新的一种算法，并没有对梯度下降中的学习率进行优化。

注意历史梯度与梯度清零的概念：清零的梯度是梯度本身，而这个缓存的历史梯度是用来作为动量计算的一个参数

AdaGrad优化法

AdaGrad（Adaptive Gradient Algorithm）为每个参数引入独立的学习率，它根据历史梯度的平方和来调整这些学习率。这种方法会逐渐减小学习率，避免了统一学习率的不足，更多用于处理稀疏数据和梯度变化较大的问题。

算法过程：

1.初始化：

​ 初始化参数$${\theta }_0$$ 和学习率 $$\eta$$并将梯度累积平方的向量 $$G_0$$ 初始化为零向量。

2.梯度计算：

​ 计算当前时间t的梯度$$g_t={\nabla }_{\theta }J({\theta }_t)$$。

3.累计梯度平方：

​
$$G_t=G_{t-1}+g_t^2$$
其中$$G_t$$ 是累积的梯度平方和，$$g_t$$ 是第$$i$$个参数在时间步$$t$$ 的梯度。

4.参数更新：

​ 利用累计的梯度平方更新参数：
$${\theta }_t={\theta }_{t-1}-\frac{\eta }{\sqrt{G_t+ϵ}}{g}_t$$
其中：

• $$\eta$$ 是全局的初始
• $$ϵ$$ 是一个非常小的常数，用于避免除零操作（通常取$$10^{-8}$$）。
• $$\frac{\eta }{\sqrt{G_t+ϵ}}$$ 是自适应调整后的学习率。

AdaGrad为每个参数分配了不同的学习率：对于较大的参数，Gt较大，学习率较小，从而避免更新过快；对于梯度较小的参数，Gt较小，学习率较大，从而加快更新速度。

方法特点：

• 自适应学习率：由于每个参数的学习率是基于其梯度的累积平方和 $$G_{t,i}$$ 来动态调整的，这意味着学习率会随着时间步的增加而减少，对梯度较大且变化频繁的方向非常有用，防止了梯度过大导致的震荡。

• 学习率过度衰减：随着时间的推移，累积的时间步梯度平方值越来越大，导致学习率逐渐接近零，模型会停止学习。

AdaGrad是一种有效的自适应学习率算法，但由于学习率衰减问题，我们将选择其他更为合适的方法。

# 使用Pytorch中的AdaGrad优化器
import torch.optim as optimopt = optim.Adagrad(model.parameters())

RMSProp优化法

​ RMSProp（Root Mean Square Propagation）是一种自适应学习率的优化算法，通过引入 指数加权平均 来累积历史梯度的平方，从而动态调整学习率，解决了AdaGrad 学习率单调递减的问题。

其公式为：
$$\begin{gathered} s_t=\beta \cdot s_{t-1}+(1-\beta )\cdot g_t^2 \\ {\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{s_t+ϵ}}\cdot gt \end{gathered}$$

• β是衰减因子，通常取 0.9。
• η是初始学习率。
• ϵ是一个小常数（通常取 $10^{-8}$），用于防止除零。
• $g_t$是当前时刻的梯度。

优点：

• RMSProp自适应调整每个参数的学习率，对于梯度变化较大的情况非常有效，使得优化过程更加平稳。
• 解决过度衰减问题：通过引入指数加权平均，RMSProp避免了AdaGrad中学习率过快衰减的问题，保持了学习率的稳定性

缺点：RMSProp的效果对衰减率 $$\alpha$$ 和学习率 $$\eta$$ 的选择比较敏感，需要不断调试得出最优参数。

# 使用Pytorch中的RMSProp优化器
import torch.optim as optim
opt = optim.RMSprop(model.parameters(), lr=0.01)

Adam优化法

Adam（Adaptive Moment Estimation）算法将动量法（Momentum）和RMSProp的优点结合在了一起，通过指数加权平均对梯度和学习率进行动态调整。

一阶动量估计（梯度的指数加权平均）：
$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$$
其中，$$m_t$$ 是当前时间步 $$t$$ 的一阶动量估计，表示梯度的指数加权平均。

二阶动量估计（梯度平方的指数加权平均）：

更新二阶动量估计：
$$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$$
其中，$$v_t$$ 是当前时间步 $$t$$ 的二阶动量估计，表示梯度平方的指数加权平均。

由于一阶动量和二阶动量在初始阶段可能会有偏差，特别是当数据数量特别小时，会导致实际结果和期望偏差过大，所以使用以下公式进行偏差校正：
$$\begin{gathered} {\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t} \\ {\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t} \end{gathered}$$
使用校正后的动量估计更新参数：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t$$
优点

1. 高效稳健：Adam结合了动量法和RMSProp的优势，在处理非静态、稀疏梯度和噪声数据时表现出色，能够快速稳定地收敛。

2. 自适应学习率：Adam通过一阶和二阶动量的估计，自适应调整每个参数的学习率，避免了全局学习率设定不合适的问题。

3. 适用大多数问题：Adam几乎可以在不调整超参数的情况下应用于各种深度学习模型，表现良好。

缺点

1. 超参数敏感：尽管Adam通常能很好地工作，但它对初始超参数（如 $${\beta }_1$$、$${\beta }_2$$ 和 $$\eta$$）仍然较为敏感，有时需要仔细调参。
2. 过拟合风险：由于Adam会在初始阶段快速收敛，可能导致模型陷入局部最优甚至过拟合。因此，有时会结合其他优化算法（如SGD）使用。

小结：Adam 中的偏差修正是为了补偿初始动量估计（指数加权平均）因历史数据不足而系统性偏低的偏差（例如m0 = 0），若不修正，模型早期梯度估计过小导致参数更新缓慢，影响训练效果，且当数据不足时，最后的梯度结果会与长期平均梯度相差很大；除了对一阶动量（梯度的平均）进行估计，Adam 还计算二阶动量（梯度平方的加权平均）来自适应调整每个参数的学习率，实现更稳定和高效的优化。对于二阶动量（梯度平方的指数加权平均）来说，不进行偏差修正会导致初期估计值偏低，使得分母$ \sqrt{\hat{v}_t} +ϵ$ 变小，导致学习率放大得不准确，可能引发参数更新不稳定。

二、常见激活函数

sigmoid激活函数

​ Sigmoid激活函数是一种经典的非线性函数，数学表达式为 $\sigma (x)=\frac{1}{1+e^{-x}}$，它将输入映射到0到1之间，常用于二分类模型的输出层以表示概率。Sigmoid函数曲线呈“S”形，输入为大正值时输出接近1，输入为大负值时输出接近0。

公式：
$$f(x)=\sigma (x)=\frac{1}{1+e^{-x}}$$
$$e$$ 是自然常数（约等于2.718），$$x$$ 是输入。

函数图像即导数图像：

)

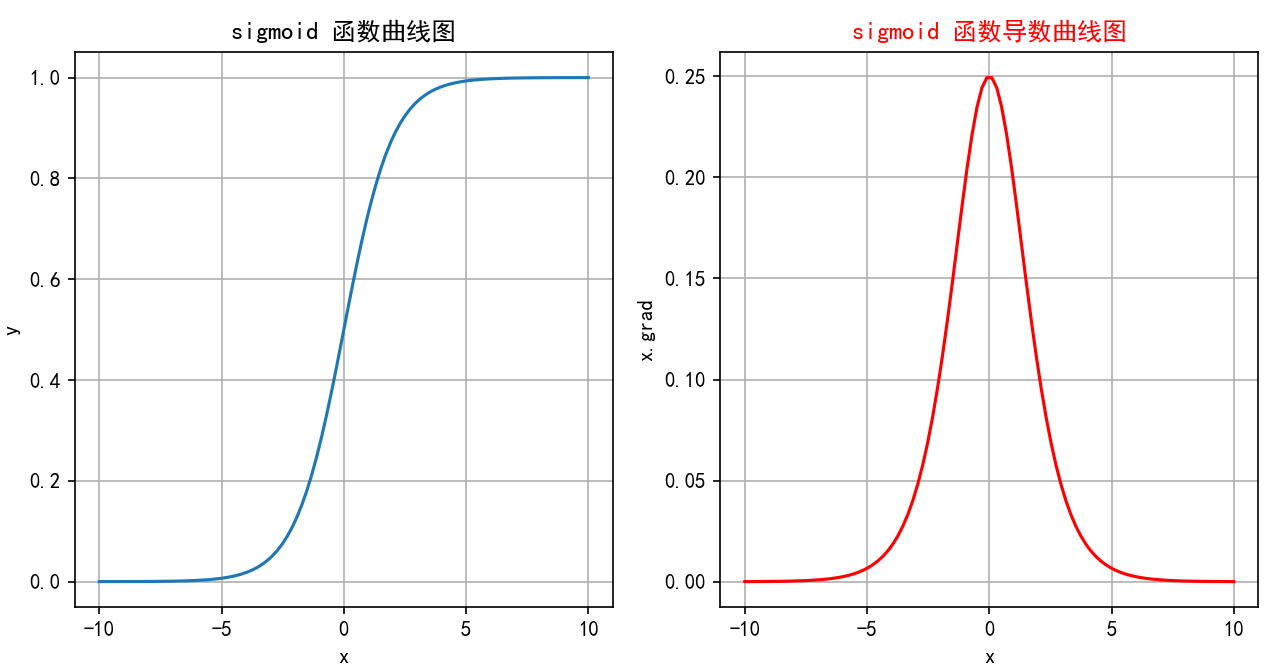
特点：

1. 将任意实数输入映射到 (0, 1)之间，因此非常适合处理概率场景。
2. 梯度消失：在输入非常大或非常小时，Sigmoid函数的梯度会变得非常小，接近于0。这导致在反向传播过程中，梯度逐渐衰减。这会使得早期层的权重更新非常缓慢，进而导致训练速度变慢甚至停滞。
3. 早期层的权重更新非常缓慢，进而导致训练速度变慢甚至停滞。

tanh激活函数

​ tanh激活函数将输入映射到 −1 到 1 之间，输出中心对称于原点，具有零均值的特点。相比于 Sigmoid，tanh 在负输入时能输出负值，能更好地缓解梯度消失问题，促进网络更快收敛。

公式：
$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
函数图像即导数图像：

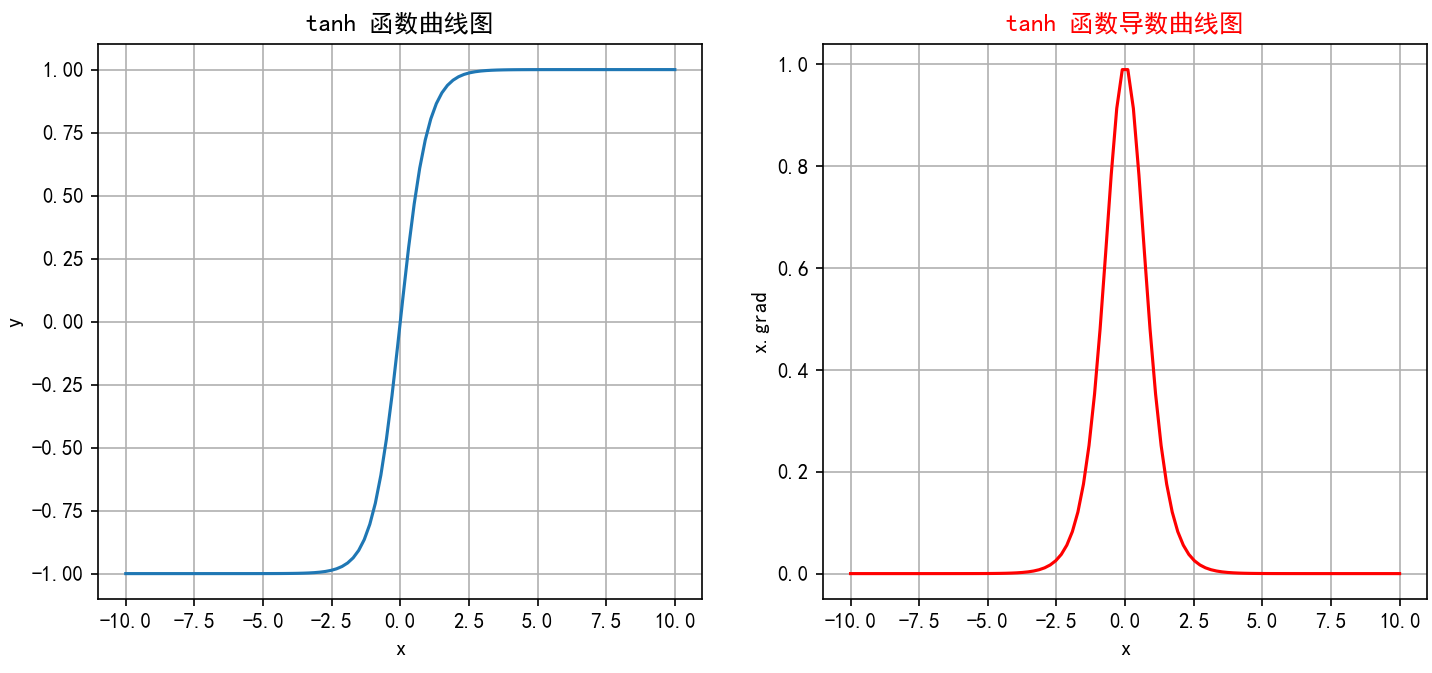
特点：

1. 梯度消失：虽然在一定程度上改善了梯度消失问题，但是其根本的问题还是没有得到解决在输入值非常大或非常小时导数还是非常小，这在深层网络中仍然是个问题。

​ 2.计算成本: 由于涉及指数运算，Tanh的计算成本还是略高，尽管 差异不大。

ReLU激活函数

​ ReLU（Rectified Linear Unit，线性整流单元）激活函数是目前深度学习中最常用的激活函数之一，它将所有负值输入映射为0，正值输入保持不变，因此计算简单且具备稀疏激活的特性。

公式：
$$\text{ReLU}(x)=\max (0,x)$$
等同于
$$\begin{gathered} \bullet \text{当 }x>0\text{ 时,ReLU}(x)=x \\ \bullet \text{当 }x\le 0\text{ 时,ReLU}(x)=0 \end{gathered}$$
函数图像即导数图像：

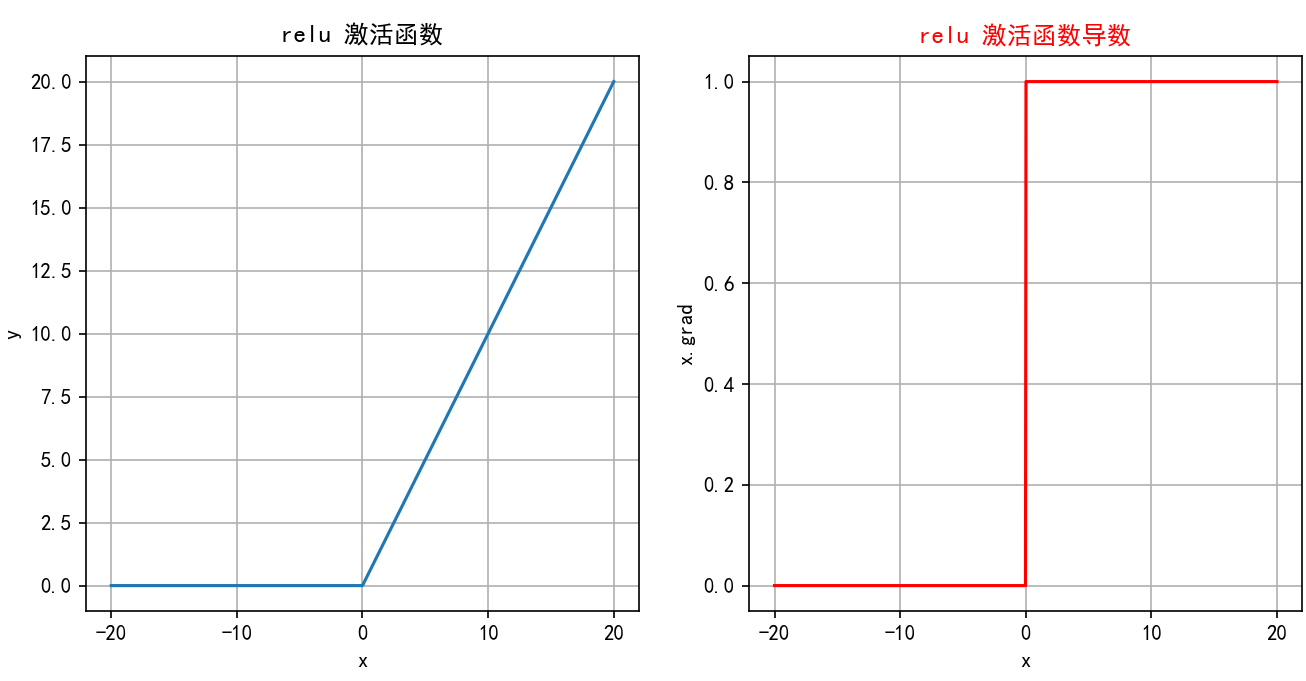
特点：

1. 计算简单：只需要对输入进行一次比较运算，在实际应用中大大加速了神经网络的训练。
2. 缓解梯度消失：相比sigmoid和tanh激活函数，ReLU 在正半区的导数恒为 1，这使得深度神经网络在训练过程中可以更好地传播梯度，不存在饱和问题。
3. 神经元死亡：由于$$ReLU$$在$$x\le 0$$时输出为$$0$$，如果某个神经元输入值是负，那么该神经元将永远不再激活，成为“死亡”神经元。随着训练的进行，网络中可能会出现大量死亡神经元，从而会降低模型的表达能力。

LeakyReLU激活函数

​ Leaky ReLU 是 ReLU 激活函数的改进版本，旨在解决 ReLU 的“神经元死亡”问题。

公式：
$$\text{Leaky ReLU}(x)=\{\begin{array}{ll}x,& \text{if }x>0\\ \alpha x,& \text{if }x\le 0\end{array}$$
其中，$\alpha $是一个很小的常数（如 0.01），表示在负输入时仍保留一小部分梯度。这样，Leaky ReLU 允许负值输入有微弱的非零输出，避免了部分神经元长期不更新的现象。它在保持 ReLU 简单高效的同时，提高了模型的鲁棒性，常用于深度神经网络中以提升训练效果。

函数图像即导数图像：

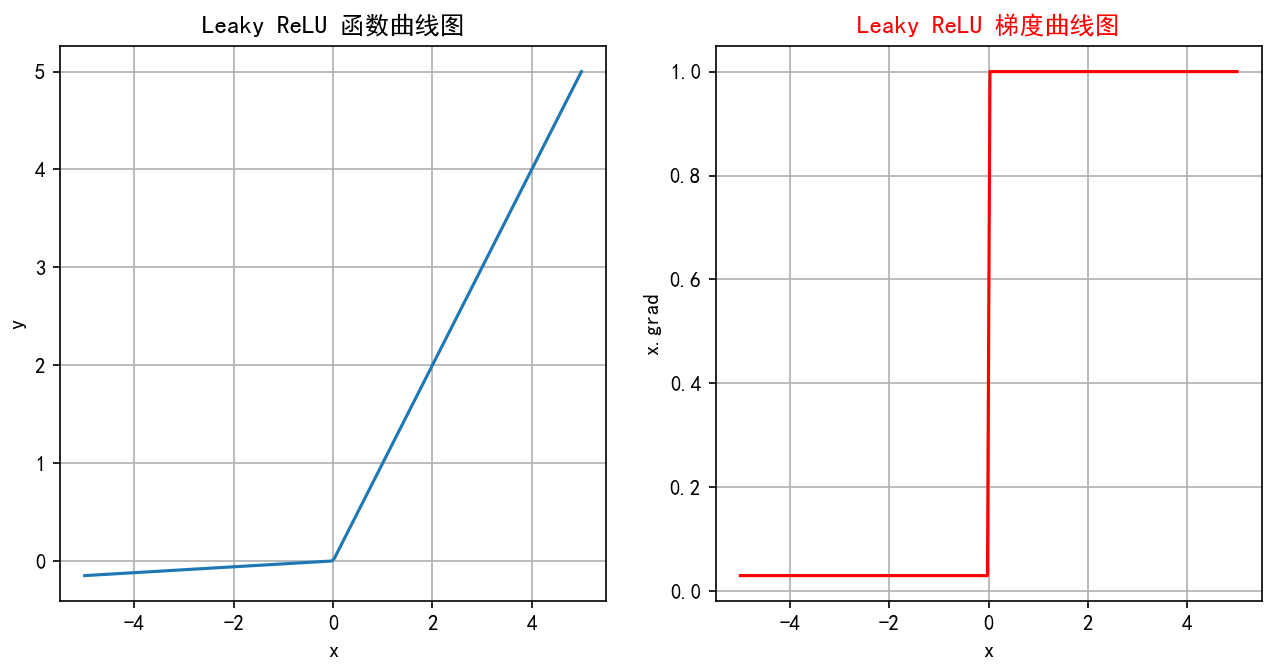
特点：

1. 避免神经元死亡：通过在$$x\le 0$$ 区域引入一个小的负斜率，即使输入值小于等于零，Leaky ReLU仍然会有梯度，允许神经元继续更新权重，避免神经元在训练过程中完全“死亡”的问题。
2. 计算简单：只需简单的比较和线性运算，计算开销低。
3. 需要进行参数调整：$$\alpha$$ 是一个需要调整的超参数，选择合适的$$\alpha$$ 值可能需要实验和调优。如果$$\alpha$$ 设定得不当，仍然可能导致激活值过低。

softmax激活函数

Softmax函数是多分类神经网络最后一层常用的激活函数，它将一个实数向量转换成一个概率分布，使得输出的各个类别的概率之和为 1，常应用在多分类问题中。

公式：

假设输出层由$$n$$个节点，每个节点的输入为$$z_i$$，则 ：
$$\mathrm{Softmax}(z_i)=\frac{e^{z_i}}{{\sum }_{j=1}^n{e}^{z_j}}$$
该公式将每个输出值设置在了(0,1)之间，并且输出值之和为1。

特点：

1. 概率分布：$$Softmax$$的输出是一个概率分布，即每个输出值$$\text{Softmax}(z_i)$$都是一个介于$$0$$和$$1$$之间的数，并且所有输出值的和为 1。
2. 将输出转化为概率：通过$$Softmax$$，可以将网络的原始输出转化为各个类别的概率，从而可以根据这些概率进行分类决策。
3. 将输出转化为概率：通过$$Softmax$$，可以将网络的原始输出转化为各个类别的概率，从而可以根据这些概率进行分类决策。
4. 在实际应用中，$$Softmax$$常与交叉熵损失函数Cross-Entropy Loss结合使用，用于多分类问题。在反向传播中，$$Softmax$$的导数计算是必需的。

softmax函数在pytorch框架中的优化：

在原本的softmax函数中，当$$z_i$$的数值过大，$$e^{z_i}$$可能会导致数值溢出。所以pytorch的框架对softmax函数进行了优化：
$$\mathrm{Softmax}(z_i)=\frac{e^{z_i-\max (z)}}{{\sum }_{j=1}^n{e}^{z_j-\max (z)}}$$
分子和分母同时除以$e^{max(z)}$。

解释：$$z_i-\max (z)$$是一个非正数，由于 $e^{z_i-max(z)}$ 的形式，当 $z_i$ 接近 max(z) 时，$e^{z_i-max(z)}$ 的值会接近 1，而当 $z_i$ 远小于 max(z) 时，$e^{z_i-max(z)}$ 的值会接近 0。这使得 Softmax 函数的输出中，最大值对应的概率会相对较大，而其他值对应的概率会相对较小，从而提高数值稳定性。这种调整不会改变$$Softmax$$的概率分布结果，因为从数学的角度讲相当于分子、分母都除以了$$e^{\max (z)}$$。

选择激活函数：

隐藏层：优先使用ReLU，如果ReLU效果不佳，在尝试其他函数，如Leaky ReLU等；避免使用sigmoid函数，尝试使用tanh函数。

输出层：二分类问题选择sigmoid函数，多分类问题选择softmax函数

更多的激活函数请参考官方文档：https://pytorch.org/docs/stable/nn.html#non-linear-activations-weighted-sum-nonlinearity

三、常见损失函数

线性回归损失函数

在之前进行机器学习的过程中，总结了两种关于线性回归的损失函数，分别是MSE损失函数和MAE损失函数。

• MSE（Mean Squared Error，均方误差），也被称为L2损失函数

，通过计算预测值和真实值之间的绝对差的平方取平均值来衡量预测他们的差异。

MSE公式：
$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2$$
特点：

1. MSE 对较大误差施加更大惩罚， 对异常值更为敏感。
2. MSE 是一个凸函数，这意味着它具有一个唯一的全局最小值，有助于优化问题的求解。

• MAE（Mean Absolute Error，平均绝对误差），也被称为L1损失函数，通过计算预测值与真实值之间的绝对差取平均值来衡量他们的差异。

MAE公式：
$$\text{MAE}=\frac{1}{n}\sum _{i=1}^n\left|y_i-{\hat{y}}_i\right|$$
特点：

1. 鲁棒性：MAE不会像MSE一样对较大的误差平方敏感，对异常值更为鲁棒。
2. MAE以与原始数据相同的单位度量误差，使其易于解释。

两者应用场景上：MAE通常用于需要对误差进行线性度量的情况，尤其是当数据中可能存在异常值时，MAE可以避免对异常值的过度惩罚。

而MSE被广泛应用在神经网络中。

交叉熵损失函数

对于多分类问题而言，输出层的结果往往是概率，对这些概率进行计算得出交叉熵公式：
$$\text{CrossEntropyLoss}(y,\hat{y})=-\sum _{i=1}^C{y}_i\log ({\hat{y}}_i)$$

• $$C$$ 是类别的总数。
• $$y$$ 是真实标签的one-hot编码向量，表示真实类别。
• $$\hat{y}$$ 是模型的输出（经过 softmax 后的概率分布）。
• $$y_i$$ 是真实类别的第 $$i$$ 个元素（0 或 1）。
• $${\hat{y}}_i$$ 是预测的类别概率分布中对应类别 $$i$$ 的概率。

其函数图形为：

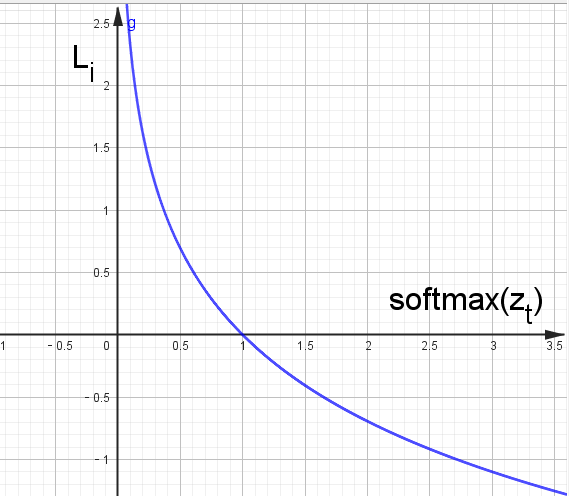
该公式表明了当预测值越大时，即样本为目标类别概率越大，函数值越小，损失低。

在实际运用交叉熵损失函数的过程中往往搭配softmax函数一起使用，使得模型的输出表示为一个概率分布，而在pytorch中的 nn.CrossEntropyLoss 就内置了softmax操作，所以如果我们在输出层中显示地调用softmax就会导致softmax被重复调用，影响模型训练效果。

在大多数多分类问题中，首档选用 nn.CrossEntropyLoss 损失函数。

nn.CrossEntropyLoss基本原理：

由交叉熵公式可知：
$$\text{Loss}(y,\hat{y})=-\sum _{i=1}^C{y}_i\log ({\hat{y}}_i)$$
因为$y_i$是one-hot编码，其值不是1便是0，又是乘法，所以只要知道1对应的index就可以了，展开后：
$$\text{Loss}(y,\hat{y})=-\log ({\hat{y}}_m)$$
其中，m表示真实类别。

因为神经网络最后一层分类总是接softmax，所以可以把${\hat{y}}_m$直接看为是softmax后的结果。
$$\text{Loss}(i)=-\log (softmax(x_i))$$
所以，CrossEntropyLoss 实质上是两步的组合：Cross Entropy = Log-Softmax + NLLLoss

• Log-Softmax：对输入 logits 先计算对数 softmax：log(softmax(x))。
• NLLLoss（Negative Log-Likelihood）：对 log-softmax 的结果计算负对数似然损失。简单理解就是求负数。原因是概率值通常在 0 到 1 之间，取对数后会变成负数。为了使损失值为正数，需要取负数。

中的reduction参数：

• ‘mean’（默认）：对所有样本的损失求平均值
• ‘sum’：将所有样本的损失加和
• ‘none’：不做聚合，返回每个样本单独的损失值，形状与输入的 batch 大小相同。

二分类BCELoss函数

二分类交叉熵损失函数公式是由上述的交叉熵公式演变而来，其针对于二分类问题，真实标签 y的值为（0 或 1），假设模型预测为正类的概率为 $\hat{y}$：
$$
\begin{cases} {y} & 如果 y=1\
1−{y} & 如果 y=0

\end{cases}
$$所以BCELoss函数：$$
\text{BCELoss}(y, \hat{y}) = -[ylog(\hat{y}) + (1-y)log(1-\hat{y})]
$$

nn.BCELoss

而在解决实际二分类问题时，BCELoss函数往往搭配sigmoid激活函数使用，如果单独使用BCELoss损失函数则需要显示调用激活函数。同nn.CrossEntropyLoss一样，二分类的交叉熵损失函数也有内置了sigmoid函数的损失函数。

nn.BCEWithLogitsLoss

总结

• 在解决多分类问题时，输出层使用softmax+交叉熵损失函数；
• 在解决二分类问题时，输出层使用sigmoid+二分类交叉熵损失函数（逻辑回归中使用的就是这种方法）；
• 当处理线性回归时，通常使用L2均方差损失函数。

四、Dropout

在之前学习机器学习的时候介绍了解决过拟合的两种正则化方法：L1正则化和L2正则化，这里我们着重降一下另一种能够解决过拟合的方法——Dropout

Dropout是一种在训练过程中随机丢弃部分神经元的技术。它作为一个特殊层（正则化层）存在于神经网络中，通过减少神经元之间的依赖来防止模型过于复杂，从而避免过拟合。

Dropout工作流程：

1.通过传入的概率参数选择一部分神经元。

2.训练过程中被选中的神经元将不参与本轮训练中的前向传播与反向传播。

3.由于训练时会随机丢弃一部分神经元，为了保证剩余神经元在整体输出上的期望值与不丢弃时一致，需要将其输出按比例放大，缩放因子为$$1/(1-p)$$，这样可以避免因随机失活导致输出整体偏小，从而保持网络在训练和推理阶段的数值分布一致。

假设某个神经元的输出为 x，Dropout 的操作可以表示为：

• 在训练阶段：
  $$y=\{\begin{array}{ll}\frac{x}{1-p}& 以概率1-p保留神经元\\ 0& 以概率p丢弃神经元\end{array}$$

• 在测试阶段：
  $$y=x$$

例如在构建自定义神经网络时使用dropout：

class MyNet(nn.Module):def __init__(self):super(MyNet, self).__init__()self.fc1 = nn.Linear(16 * 26 * 26, 256)self.bn1 = nn.BatchNorm1d(256)self.relu = nn.LeakyReLU()self.fc2 = nn.Linear(256, 512)self.bn2 = nn.BatchNorm1d(512)self.fc3 = nn.Linear(512, 10)self.dropout = nn.Dropout(0.35)def forward(self, x):x = self.bn1(self.fc1(x))x = self.relu(x)x = self.dropout(self.bn2(self.fc2(x)))x = self.relu(x)x = self.fc3(x)return x

以上内容是博主学习深度学习的一些总结笔记，若文章中出现错误请及时指正博主，感谢浏览☆噜~☆