衡量机器学习模型的指标
为了进一步了解模型的能力,我们需要某个指标来衡量,这就是性能度量的意义。有了一个指标,我们就可以对比不同的模型了,从而知道哪个模型相对好,哪个模型相对差,并通过这个指标来进一步调参以逐步优化我们的模型。
1. 正确率、精确率和召回率
假设你有一台用来预测某种疾病的机器,这台机器需要用某种疾病的数据作为输入,输出只可能是两种信息之一:有病或者没病。虽然机器的输出只有两种,但是其内部对疾病的概率估计p是一个实数。机器上还有一个旋钮用来控制灵敏度阈值a。因此预报过程是这样子:首先用数据计算出p,然后比较p和a的大小,p>a输出有病(检测结果为阳性),p<a就输出没病(检测结果为阴性)。
如何评价这台机器的疾病预测性能呢?这里就要注意了,并不是每一次都能准确预报的机器就是好机器,因为它可以次次都预报有疾病(把a调很低),自然不会漏掉,但是在绝大多数时候它都只是让大家虚惊一场,称为虚警;相反,从不产生虚警的机器也不一定就是好机器,因为它可以天天都预报没有病(把a调很高)——在绝大数时间里这种预测显然是正确的,但也必然漏掉真正的病症,称为漏报。一台预测能力强的机器,应该同时具有低虚警和低漏报。精确率高意味着虚警少,能保证机器检测为阳性时,事件真正发生的概率高,但不能保证机器检测为阴性时,事件不发生。相反,召回率高意味着漏报少,能保证机器检测为阴性时,事件不发生的概率高,但不能保证机器检测为阳性时,事件就一定发生。
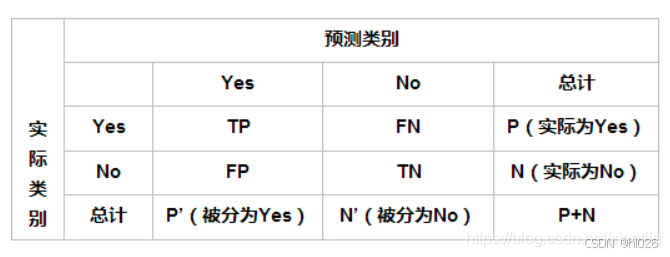
先介绍几个常见的模型评估术语,现在假设分类目标只有两类,正例(Positive)和负例(Negative)分别是:
- 真正例(True Positives, TP):模型正确预测为正类的样本数。
- 真负例(True Negatives, TN):模型正确预测为负类的样本数。
- 假正例(False Positives, FP):模型错误预测为正类的样本数(实际上是负类)。
- 假负例(False Negatives, FN):模型错误预测为负类的样本数(实际上是正类)。
(1)正确率(Accuracy)=(TP+TN)/(所有样本数P+N),最常见的评价指标,适用于样本均衡分布的情况,衡量整体分类准确性,即所有正确预测的样本数占总样本数的比例。
(2)错误率(Error Rate)=(FP+FN)/(所有样本数P+N),与正确率相反,描述被分类器错分的比例,对某一个实例来说,分对与分错是互斥事件。
(3)灵敏度(Sensitive)=TP/P,表示的是所有正例中被分对的比例,衡量了分类器对正例的识别能力。
(4)特效度(Specificity)=TN/N,表示的是所有负例中被分对的比例,它衡量了分类器对负例的识别能力。
(5)精确度(Precision)=TP/(TP+FP),也叫精度,针对预测结果而言,衡量模型预测为正类的样本中实际为正类的比例,反映了预测为正类的准确性。
(6)召回率(Recall)=TP/(TP+FN)=TP/P=灵敏度Sensitive,针对原来的样本而言,表示的是样本中的正例有多少被预测正确了,度量有多少个正例被分为正例。
比如我们一个模型对15个样本进行预测,然后结果如下: 真实值:0 1 1 0 1 1 0 0 1 0 1 0 1 0 0 预测值:1 1 1 1 1 0 0 0 0 0 1 1 1 0 1

精度(precision, 或者PPV, positive predictive value) = TP / (TP + FP)= 5 / (5+4) = 0.556
召回(recall, 或者敏感度,sensitivity,真阳性率,TPR,True Positive Rate) = TP / (TP + FN)
在上面的例子中,召回 = 5 / (5+2) = 0.714
特异度(specificity,或者真阴性率,TNR,True Negative Rate) = TN / (TN + FP)
在上面的例子中,特异度 = 4 / (4+2) = 0.667