力扣.870优势洗牌解决方法: 下标排序编辑力扣.942增减字符串匹配最长回文子序列牛客.背包问题(最大体积)力扣.45跳跃游戏II 另一种思考
目录
力扣.870优势洗牌
解决方法: 下标排序编辑
力扣.942增减字符串匹配
最长回文子序列
牛客.背包问题(最大体积)
力扣.45跳跃游戏II
另一种思考
力扣.870优势洗牌
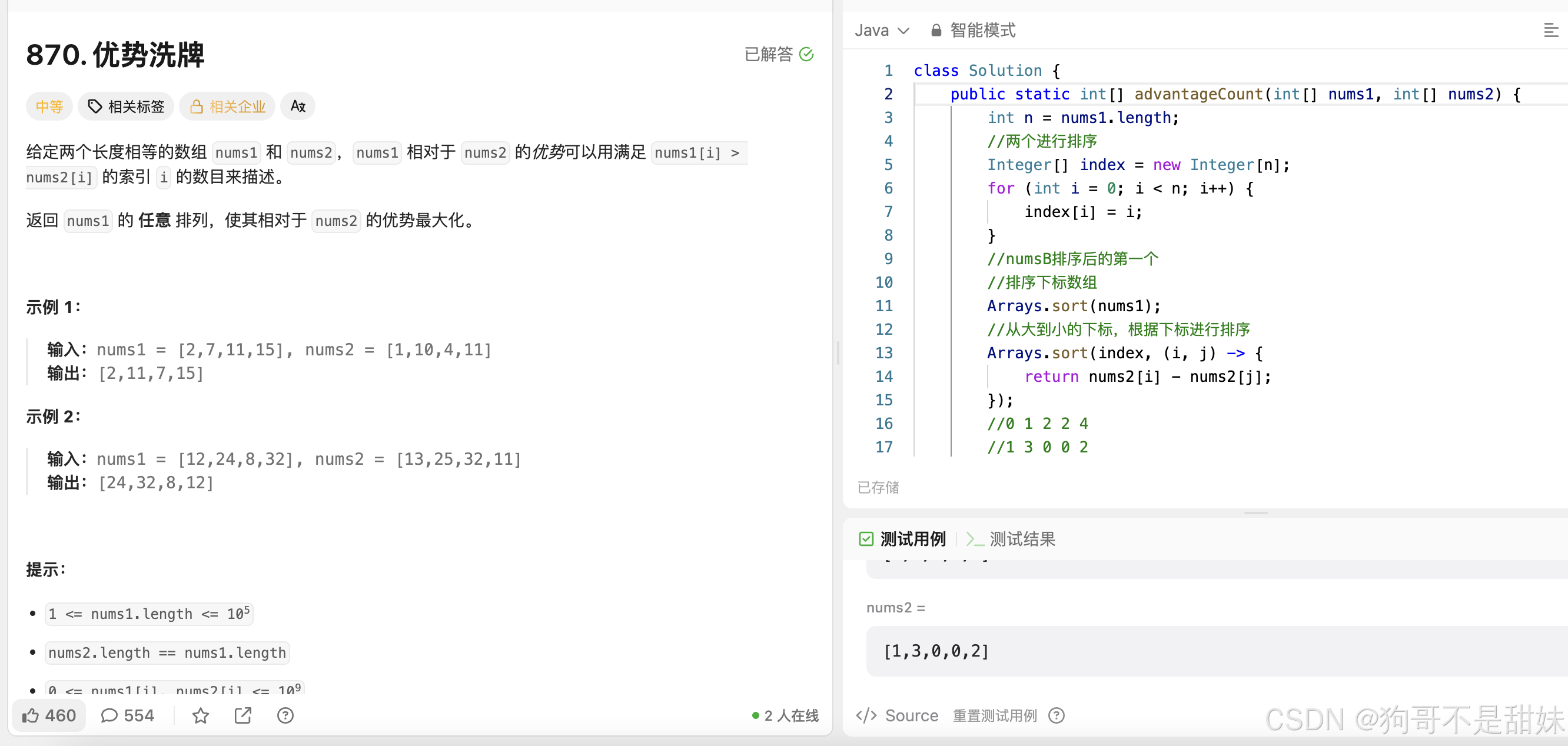
对两个进行排序
难点:排序后,如何找到之前的顺序,进行返回呢
解决方法: 下标排序
通过下标来查找,
然后定义left和right指针,假如比他大就正常给left,否则移动到right里面
感觉下标排序常用,但是不好想。
index[left]就是当前从小到大的下标,也相当于排序,但是不改变原数组
所以相当于从原数组里面排序了找,从小到大找,然后用看是否大于当前值,大于,直接给ret[[]]对应的下标值++,否则给right赋值,就是给最大的那些数
class Solution {public static int[] advantageCount(int[] nums1, int[] nums2) {int n = nums1.length;//两个进行排序Integer[] index = new Integer[n];for (int i = 0; i < n; i++) {index[i] = i;}//numsB排序后的第一个//排序下标数组Arrays.sort(nums1);//从大到小的下标,根据下标进行排序Arrays.sort(index, (i, j) -> {return nums2[i] - nums2[j];});//0 1 2 2 4//1 3 0 0 2//[2 3 0 4 1]int[] ret = new int[n];int left = 0;int right = n - 1;//从nums1遍历for (int x : nums1) {if (x > nums2[index[left]]) {ret[index[left++]] = x;} else {//比不过ret[index[right--]] = x;}}return ret;}
}力扣.942增减字符串匹配
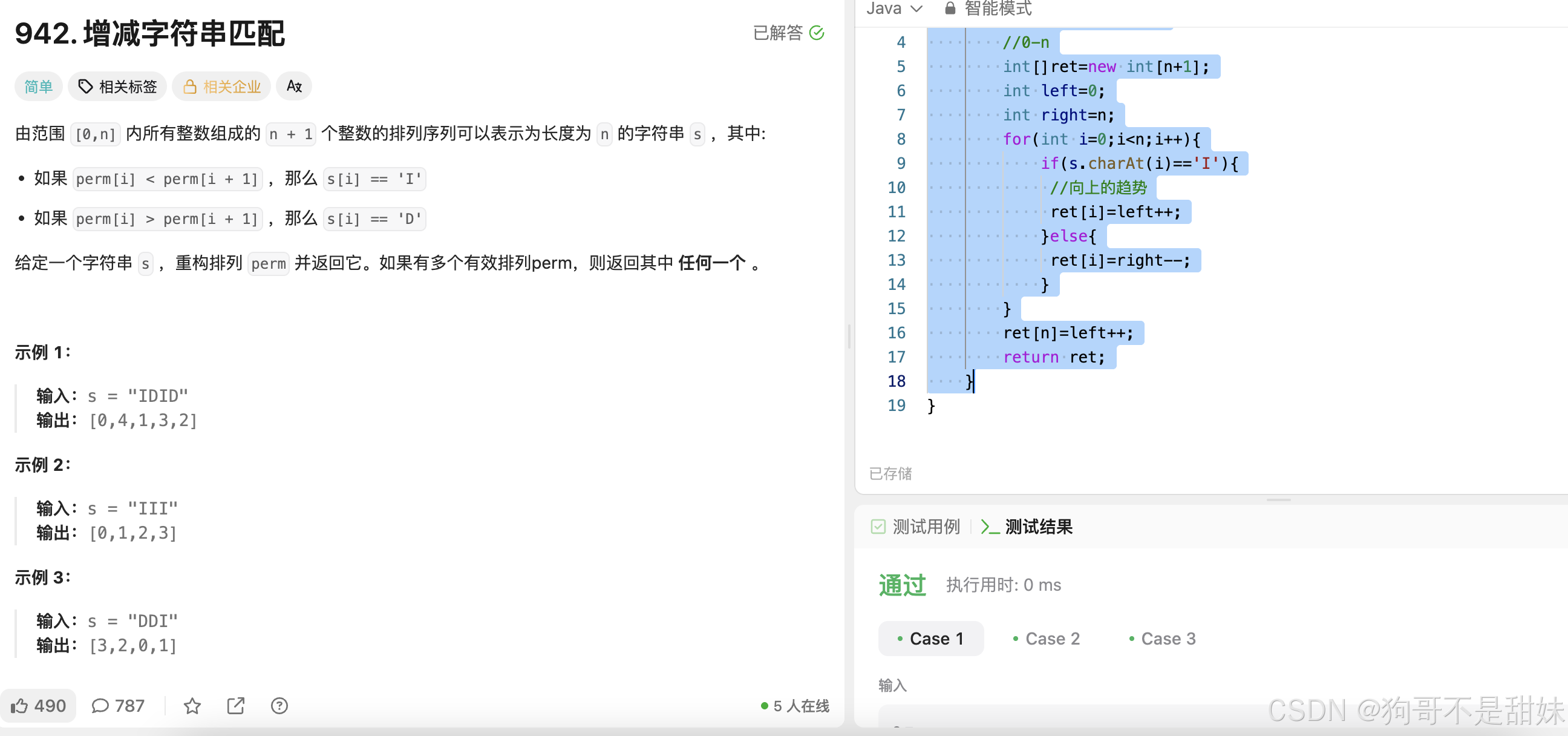
假如当前是I,就是上升的趋势,我直接取最小值上升,假如是d,就是下降的趋,我取最大值下降,为啥是正确的呢?假如当前是I,那么就要给他安排最小的,因为假如上升趋势
I [ ]框里面的每个都是上升趋势,假如d[] 框里面每个都是下降趋势
public int[] diStringMatch(String s) {int n=s.length();//0-nint[]ret=new int[n+1];int left=0;int right=n;for(int i=0;i<n;i++){if(s.charAt(i)=='I'){//向上的趋势ret[i]=left++;}else{ret[i]=right--;}}ret[n]=left++;return ret;}最长回文子序列
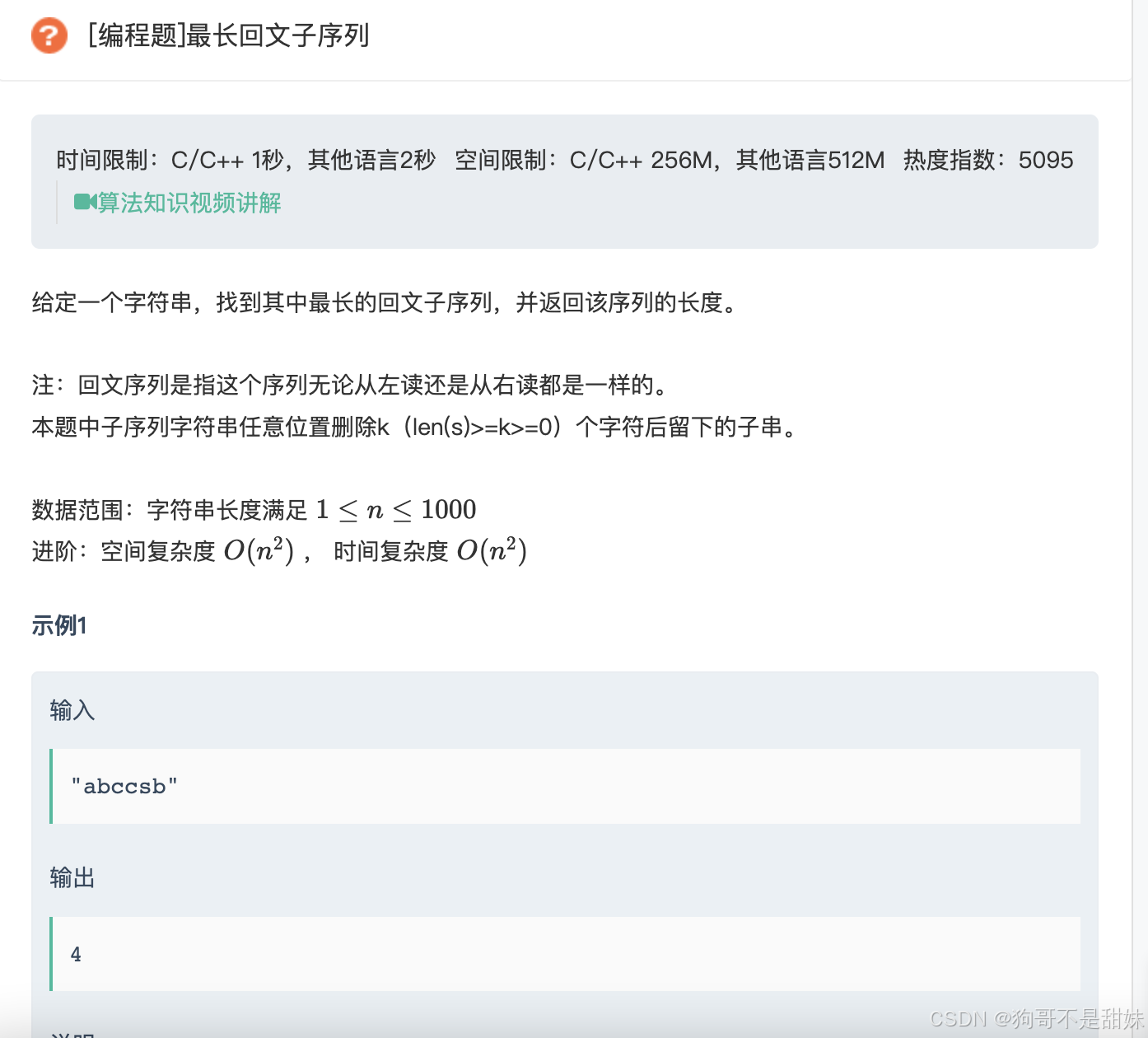
看到回文,子序列有点没反应过来,有试过一维dp,忘了二维dp怎么写了,
class Solution {public int longestPalindromeSubseq(String s) { //dp[i][j]:从i位置到j区间内的最长回文子序列 //dp[i][j]=dp[i+1][j-1]+2; //dp[i][j]=max(dp[i+1][j],dp[i][j-1]) //dp[0][0]:0->0=1 dp[0][1]= //dp[] i<j 从左往右,上半图 返回最大值int n=s.length();char[]ss=s.toCharArray();int[][]dp=new int[n][n];dp[0][0]=1;dp[n-1][n-1]=1;for(int i=n-1;i>=0;i--){for(int j=i;j<n;j++){if(ss[i]==ss[j]){if(i==j) dp[i][j]=1;else{dp[i][j]=dp[i+1][j-1]+2;}}else {dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);}}}return dp[0][n-1];} }
牛客.背包问题(最大体积)

跟我想的基本一样,就是到达i位置的时候,总体积不超过是j,然后剩余空间最小的dp[i][j].
这个的缺点就是需要进行初始化,因为最开始我的剩余体积是24
import java.util.*;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {//背包问题public static void main(String[] args) {Scanner in = new Scanner(System.in);int V=in.nextInt();int n=in.nextInt();int[]a=new int[n+1];for(int i=1;i<=n;i++){a[i]=in.nextInt();}//到达i位置时,空间为j,是剩余空间最小int[][]dp=new int[n+1][V+1];//第0个位置,此时的剩余空间是Vdp[0][V]=V;int min=V;Arrays.fill(dp[0],V);//在第一个开始时候,空间是Vfor(int i=1;i<=n;i++){for(int j=V;j>=0;j--){//塞不进去,保持不动就好dp[i][j]=dp[i-1][j];if(j-a[i]>=0){//此时说明我还能塞,或者看我能不能塞下dp[i][j]=Math.min(dp[i-1][j],dp[i-1][j-a[i]]-a[i]);}min=Math.min(min,dp[i][j]);}}System.out.print(min);}
}这个的优点就很明显,不用去初始化,但是结果需要自己处理,总结就是二者都可以
import java.util.*;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {//背包问题public static void main(String[] args) {Scanner in = new Scanner(System.in);int V=in.nextInt();int n=in.nextInt();int[]a=new int[n+1];for(int i=1;i<=n;i++){a[i]=in.nextInt();}//到达i位置时,空间为j,是剩余空间最小int[][]dp=new int[n+1][V+1];//第0个位置,此时的剩余空间是Vint max=0;// Arrays.fill(dp[0],V);//在第一个开始时候,空间是Vfor(int i=1;i<=n;i++){for(int j=V;j>=0;j--){//塞不进去,保持不动就好dp[i][j]=dp[i-1][j];if(j-a[i]>=0){//此时说明我还能塞,或者看我能不能塞下dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-a[i]]+a[i]);}max=Math.max(max,dp[i][j]);}}System.out.print(V-max);}
}力扣.45跳跃游戏II

假如用动态规划做
//到达i位置时候最小的跳跃次数
dp[i]
转移方程不是常见的那种,要去检测
从0-i-1位置中,能到达i位置
从j开始遍历 0-j j<i;j++
dp[i]=dp[j]+1;开始,第一次,后面的时候dp[i]!=0的时候,就去比较,这么多次dp[j]+1的最小值
class Solution {public int jump(int[] nums) {int n=nums.length;int[]dp=new int[n];dp[0]=0;//到达i位置时候最小的跳跃次数for(int i=1;i<n;i++){for(int j=0;j<i;j++){if(j+nums[j]>=i){if(dp[i]!=0) dp[i]=Math.min(dp[j]+1,dp[i]);else dp[i]=dp[j]+1;}}}return dp[n-1]; } }
贪心
class Solution {public static int jump(int[] a) {int n=a.length;int count=1;if(n==1)return 0;else if(a[0]>=n-1)return 1;for(int i=0;i<n;){//从i+1开始遍历int left=i+1;//右边界int right=a[i]+i;int max=0;//表示下一轮下标的值int j=0;//统计新一轮的值while(left<n&&left<=right){if(max<left+a[left]){j=left;max=left+a[left];}left++;}count++;//i取当前位置能跳的最远的值i=j;if(max>=n-1)break;}return count;} }
另一种思考
dp[i][j]:从前i个数中挑选,所有做法中,能否凑成j这个数字-true/false
状态转移方程
dp[i][j]= 不选i dp[i-1][j]
选i dp[i-1][j-a[i]] 两个取||为判断是否能凑成这个数字
初始化,假如前不管几个,我都不选,那么我都【i】count都为true;
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);int n=in.nextInt();int[]a=new int[n+1];int count=0;for(int i=1;i<=n;i++){a[i]=in.nextInt();count+=a[i];} if(count%2!=0){System.out.print(false);}else{count=count/2;int ret=0;boolean[][]dp=new boolean[n+1][count+1];for(int i=0;i<=n;i++)dp[i][0]=true;//前i个物品中,最大体积//dp[i][j]=-1表示没有这种情况for(int i=1;i<=n;i++){for(int j=0;j<=count;j++){dp[i][j]=dp[i-1][j];if(j-a[i]>=0){//指当前体积+a[i];dp[i][j]=dp[i][j]||dp[i-1][j-a[i]];}//状态,假如当前不存在和存在两种}}if(dp[n][count]==true) System.out.print(true);else System.out.print(false);}} }

