当前位置：首页 > news >正文

AI基础与实践专题：PyTorch实现线性回归

news 2025/8/12 7:42:05

往期AI基础与实践专题回顾：

        PyTorch实现手写数字识别

        AI基础与实践专题：神经网络基础

        AI基础与实践专题：PyTorch深度学习入门

前言

随着数据科学和人工智能的快速发展，机器学习在各行各业的应用日益广泛。其中，房价预测作为一个经典的回归问题，不仅有着实际的商业价值，也适合作为入门机器学习算法的示例。

本文将通过线性回归模型，结合房价数据，带你一步步理解如何构建、训练并评估一个简单有效的房价预测模型

主要内容介绍

本文主要围绕以下几个方面展开：

线性回归基础 — 理解线性回归模型的数学原理与核心思想。
数据准备与特征工程 — 介绍房价数据的基本特征及常见的数据预处理方法。
模型构建与训练 — 以Python实现线性回归训练过程，包含正规方程与梯度下降两种方法。
模型评估与结果分析 — 使用指标评估模型性能，并可视化分析结果。
总结与后续改进方向 — 总结本次案例的重点，并对未来优化提出建议。

一、线性回归基础

1、线性回归的概念

线性回归（Linear Regression）是最基础的监督学习算法之一，可以看作是只有输入层和输出层的最简单神经网络。

它的核心思想是：

$\hat{y} = w x + b$

通过学习权重 $w$ 和偏置 $b$ ，使得预测值 $\hat{y}$ 尽量接近真实值 $y$ 。

输入层：输入特征 $x$
输出层：输出预测值 $\hat{y}$
激活函数：没有（直接线性映射）

2、算法核心流程

假设函数（模型）
- 对于单变量：
  
  $\hat{y} = w x + b$
- 对于多变量：
  
  $\hat{y} = \mathbf{w}^T \mathbf{x} + b$
损失函数
- 常用 均方误差（MSE）：
  
  $L(w, b) = \frac{1}{n} \sum_{i=1}^n (\hat{y}_i - y_i)^2$
  
  它衡量预测值和真实值之间的平均平方差。
优化方法
梯度下降（Gradient Descent）：不断调整 w 和 b 使损失最小。
- 权重更新公式：
  
  $w := w - \alpha \frac{\partial L}{\partial w}$
  
  $b := b - \alpha \frac{\partial L}{\partial b}$
  
  其中 \alpha 是学习率。
训练过程
1. 初始化参数 $w, b$ （可随机）
2. 计算预测值 $\hat{y}$
3. 计算损失 L
4. 计算梯度
5. 更新参数
6. 循环直到损失收敛

3、与神经网络的关系

线性回归可以看作单层、无激活函数的神经网络。
在更复杂的神经网络中，每个神经元的线性部分都是类似的：

$z = w x + b$

然后再经过激活函数进行非线性变换。

下面用 房价预测 这个经典案例，带你从数据、建模、数学原理、实现到诊断与改进一步步理解线性回归。我要尽量把理论和实操结合起来，方便你上手复现或迁移到真实数据上。

4、房价问题概述（问题定义）

目标：用房屋的若干特征（如面积、卧室数、地段、建成年代等）来预测房价 $y$ 。

把它看作回归问题：给定 $x$ （特征向量），求模型 $\hat y = f(x)$ 。线性回归假设 $f$ 是线性的：

$\hat y = w_1 x_1 + w_2 x_2 + \dots + w_p x_p + b$

其中每个系数 $w_j$ 表示对应特征对房价的边际影响（其它特征不变时）。

数据与特征（工程要点）

常见特征举例：

连续数值：建筑面积（sqft）、土地面积、房间数、卫浴数、建成年代、楼层
类别特征：街区/小区（neighborhood）、房屋类型（独栋/公寓）
定位信息：经纬度（lat, lon）或邮编
环境/便利：到地铁/学校/超市距离、学区评分

常见预处理：

处理缺失值（删除、均值/中位数填充、基于模型填充）
对类别用 one-hot 或 target encoding 编码（街区通常 one-hot 会非常稀疏，可考虑基于统计量编码）
特征缩放（StandardScaler）——对梯度方法或正则化有帮助
处理目标（房价）偏态：对数变换 \log(y) 常用于降低异方差并使误差更接近正态

注意：地段（location）通常是决定房价的最关键因子，编码和表示方式很重要（直接 one-hot、经纬度与空间模型、或使用街区平均价格）。

二、利用PyTorch实现房价预测

1、数据的准备以及特征提取

1、载入所需要的头文件（库）
##载入所需的头文件
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
2、下载数据和检查数据格式
!wget https://model-community-picture.obs.cn-north-4.myhuaweicloud.com/ascend-zone/notebook_datasets/fb53911ce74d11efa3a4fa163edcddae/modified_file.csv
##利用pandas打印数据
df = pd.read_csv('modified_file.csv', delimiter=',', encoding='utf-8')
# 打印DataFrame的前几行
df.head(10)
打印数据格式如下：

longitude latitude housingMedianAge totalRooms totalBedrooms population households medianIncome medianHouseValue
0 -122.23 37.88 41.0 8.800 1.290 322.0 1.260 8.3252 4.526
1 -122.22 37.86 21.0 7.099 1.106 2401.0 1.138 8.3014 3.585
2 -122.24 37.85 52.0 1.467 1.900 496.0 1.770 7.2574 3.521
3 -122.25 37.85 52.0 1.274 2.350 558.0 2.190 5.6431 3.413
4 -122.25 37.85 52.0 1.627 2.800 565.0 2.590 3.8462 3.422
5 -122.25 37.85 52.0 9.190 2.130 413.0 1.930 4.0368 2.697
6 -122.25 37.84 52.0 2.535 4.890 1094.0 5.140 3.6591 2.992
7 -122.25 37.84 52.0 3.104 6.870 1157.0 6.470 3.1200 2.414
8 -122.26 37.84 42.0 2.555 6.650 1206.0 5.950 2.0804 2.267
9 -122.25 37.84 52.0 3.549 7.070 1551.0 7.140 3.6912 2.611

	longitude	latitude	housingMedianAge	totalRooms	totalBedrooms	population	households	medianIncome	medianHouseValue
0	-122.23	37.88	41.0	8.800	1.290	322.0	1.260	8.3252	4.526
1	-122.22	37.86	21.0	7.099	1.106	2401.0	1.138	8.3014	3.585
2	-122.24	37.85	52.0	1.467	1.900	496.0	1.770	7.2574	3.521
3	-122.25	37.85	52.0	1.274	2.350	558.0	2.190	5.6431	3.413
4	-122.25	37.85	52.0	1.627	2.800	565.0	2.590	3.8462	3.422
5	-122.25	37.85	52.0	9.190	2.130	413.0	1.930	4.0368	2.697
6	-122.25	37.84	52.0	2.535	4.890	1094.0	5.140	3.6591	2.992
7	-122.25	37.84	52.0	3.104	6.870	1157.0	6.470	3.1200	2.414
8	-122.26	37.84	42.0	2.555	6.650	1206.0	5.950	2.0804	2.267
9	-122.25	37.84	52.0	3.549	7.070	1551.0	7.140	3.6912	2.611

df.describe（）
数据文件信息如下：
<bound method NDFrame.describe of        longitude  latitude  housingMedianAge  totalRooms  totalBedrooms  \
0        -122.23     37.88              41.0       8.800          1.290   
1        -122.22     37.86              21.0       7.099          1.106   
2        -122.24     37.85              52.0       1.467          1.900   
3        -122.25     37.85              52.0       1.274          2.350   
4        -122.25     37.85              52.0       1.627          2.800   
...          ...       ...               ...         ...            ...   
20635    -121.09     39.48              25.0       1.665          3.740   
20636    -121.21     39.49              18.0       6.970          1.500   
20637    -121.22     39.43              17.0       2.254          4.850   
20638    -121.32     39.43              18.0       1.860          4.090   
20639    -121.24     39.37              16.0       2.785          6.160   population  households  medianIncome  medianHouseValue  
0           322.0       1.260        8.3252             4.526  
1          2401.0       1.138        8.3014             3.585  
2           496.0       1.770        7.2574             3.521  
3           558.0       2.190        5.6431             3.413  
4           565.0       2.590        3.8462             3.422  
...           ...         ...           ...               ...  
20635       845.0       3.300        1.5603             0.781  
20636       356.0       1.140        2.5568             0.771  
20637      1007.0       4.330        1.7000             0.923  
20638       741.0       3.490        1.8672             0.847  
20639      1387.0       5.300        2.3886             0.894  [20640 rows x 9 columns]>
这里我们把最后一列的房价信息当作我们的标签值，而其他列的数据则作为我们的输入特征，依靠神经网络进行特征提取，找到房价与各特征之间的关系

最后一列 medianHouseValue（中位房价） 作为标签（目标变量），即模型要预测的房价。

其余列（比如经度 longitude，纬度 latitude，房屋中位年龄 housingMedianAge，总房间数 totalRooms，总卧室数 totalBedrooms，人口 population，户数 households，中位收入 medianIncome）作为输入特征（自变量）。

利用神经网络模型，通过训练让模型学会从这些输入特征中提取有效信息（特征提取），进而找到它们和房价之间的复杂关系，从而预测新的样本的房价。

简单来说就是：

输入（多个特征） → 神经网络 → 输出（预测房价）

2、数据集的划分以及数据加载

\训练集测试集的划分 --> 使用skelearn库
coff = df.iloc[:,:-1];###关注的特征
tar = df.iloc[:,-1]; ##房价coff_train,tar_train,coff_test,tar_test = train_test_split(coff,tar,test_size= 0.33,random_state=1 )# 固定随机种子，保证数据划分结果可复现
input_scalar = StandardScaler();
output_scalar = StandardScaler();
##标准化工具
coff_train = input_scalar.fit_transform(coff_train).T;
coff_test = input_scalar.transform(coff_test).T;
tar_train = input_scalar.fit_transform(coff_train).T;
tar_test = input_scalar.transform(tar_test).T;
1. x_train = input_scalar.fit_transform(x_train).

input_scalar 通常是一个用于数据标准化的对象，比如 sklearn.preprocessing.StandardScaler()。

.fit_transform(x_train) 作用是：

fit：计算 x_train 中每个特征的均值和标准差（这两个参数会被保存下来）。

transform：根据刚才计算的均值和标准差，对 x_train 做标准化处理（即对每个特征值减均值除以标准差）。

.T 是转置操作，把训练集特征矩阵的形状转成(特征数, 样本数)，这通常是因为后续模型输入要求这样的格式。

总结：对训练数据做标准化并转置。

        2. x_test = input_scalar.transform(x_test).T

注意这里没有 .fit_transform，而只是 .transform。

这是为了避免数据泄露（data leakage）：测试集的标准化必须基于训练集的均值和标准差进行转换，而不是重新计算。

同样做转置操作。

总结：用训练集标准化参数标准化测试集，并转置

问题：为什么测试集不能用 .fit_transform()，只能用 .transform()？

避免数据泄露（Data Leakage）：

        测试集本质上是用来模拟“真实环境下模型遇到的新数据”。如果在标准化时用测试集本身去计算均值和标准差（即 .fit()），模型就“提前知道”了测试集的统计信息，这样就泄露了测试集信息，导致评估结果不真实。

保证训练和测试数据处理一致：

训练集和测试集的分布是相似的，所以用训练集的均值和标准差去标准化测试集，确保两者的尺度一致。

如果测试集用自己的均值和标准差去标准化，数据尺度就不一样，模型性能的评价可能会失真。

        3. y_train = output_scalar.fit_transform(y_train).reshape(-1)

对训练标签（目标值）y_train 做标准化处理。

fit_transform：计算训练标签的均值和标准差并做转换。

.reshape(-1) 把结果转换成一维数组，方便模型训练时输入

4. y_test = output_scalar.transform(y_test).reshape(-1)

同样，测试标签只做转换，不重新计算参数。

维度也调整为一维数组

为什么要对输入和输出都做标准化？

输入特征：不同特征量纲不一样，标准化能让每个特征“权重”更均衡，避免某些特征因量纲太大而主导训练。

输出标签：对于回归问题，标准化标签能帮助模型更快收敛，尤其是当标签数值范围差别较大时

3、神经网络（线性回归器）的搭建

###定义我们的线性回归类
class linear_regression():def __init__(self,dim,lr = 0.1):self.lr = lr;self.w = np.zeros((dim));self.grads = {"dw" : np.zeros((dim)) + 5};##创建字典存储梯度矩阵def forward(self,x):y = self.w.T @ x;return ydef backward(self,x,y_hat,y):assert y_hat.shape == y.shape;self.grads["dw"] = (1 / x.shape[1]) * ((y_hat - y) @ x.T).Tassert self.grads["dw"].shape == self.w.shape;def optimizer(self):self.w = self.w - lr*self.grads["dw"];

这里定义了我们的权重矩阵，梯度权重矩阵，前向和反向传播算法。

4、训练参数设置和训练

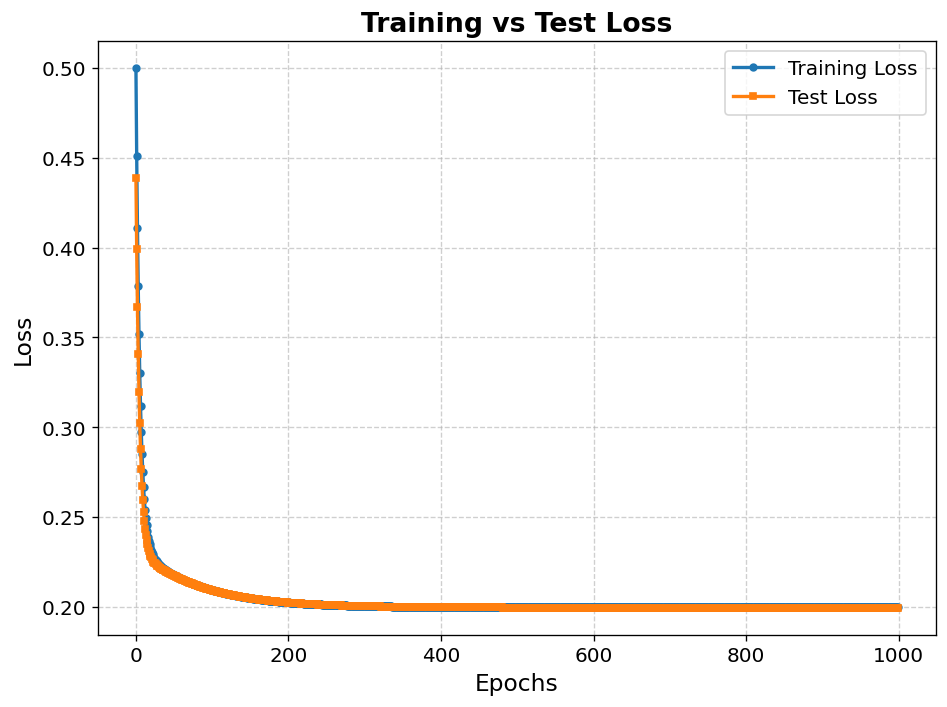
### 开始训练，参数的定义
num_epochs = 1000;
dim = coff_train.shape[0];
train_loss_history = [];
test_loss_history = [];
w_history =[];
num_train = coff_train.shape[1];
num_test = coff_test.shape[1];
lr 
model = linear_regression(dim,lr = 0.1);
for i in range(num_epochs):####训练集y_hat = model.forward(coff_train);train_loss = ((tar_train - y_hat)**2).sum()/(2*num_train);w_history.append(model.w);
#     print("y_hat shape:", y_hat.shape)
#     print("tar_train shape:", tar_train.shape)model.backward(coff_train,y_hat,tar_train)model.optimizer();####测试集y_hat = model.forward(coff_test);test_loss = ((tar_test - y_hat)**2).sum()/(2*num_test);train_loss_history.append(train_loss)test_loss_history.append(test_loss)if i % 20 == 0:print(f"Epoch {i} | Train Loss {train_loss} | Test Loss {test_loss}")

这里定义了1000个训练周期，定义的损失函数为常规的MSE损失函数。

输出结果及可视化：

poch 0 | Train Loss 0.4999999999999999 | Test Loss 0.4385709557441168
Epoch 20 | Train Loss 0.23155592118127374 | Test Loss 0.22747287991136736
Epoch 40 | Train Loss 0.22027307961690287 | Test Loss 0.2195193741305869
Epoch 60 | Train Loss 0.21558861443906438 | Test Loss 0.21528849452502388
Epoch 80 | Train Loss 0.21206482263627935 | Test Loss 0.21187488396756804
Epoch 100 | Train Loss 0.20932658412179803 | Test Loss 0.20918250106064035
Epoch 120 | Train Loss 0.20719378244078954 | Test Loss 0.20707537769918252
Epoch 140 | Train Loss 0.20553161386575025 | Test Loss 0.2054287322517851
Epoch 160 | Train Loss 0.20423581523869258 | Test Loss 0.20414204147058299
Epoch 180 | Train Loss 0.20322541980949602 | Test Loss 0.2031364117577128
Epoch 200 | Train Loss 0.20243745464312454 | Test Loss 0.20235024181461067
Epoch 220 | Train Loss 0.20182289432960243 | Test Loss 0.20173546786782337
Epoch 240 | Train Loss 0.20134354696349765 | Test Loss 0.2012545829391712
Epoch 260 | Train Loss 0.20096964704321188 | Test Loss 0.20087831000857748
Epoch 280 | Train Loss 0.20067798937695516 | Test Loss 0.20058379051150507
Epoch 300 | Train Loss 0.20045047951844747 | Test Loss 0.20035317364319333
Epoch 320 | Train Loss 0.20027300622749628 | Test Loss 0.2001725169793004
Epoch 340 | Train Loss 0.20013456360447066 | Test Loss 0.20003092916203988
Epoch 360 | Train Loss 0.200026567182549 | Test Loss 0.19991990104214577
Epoch 380 | Train Loss 0.19994232089658304 | Test Loss 0.1998327836847065
Epoch 400 | Train Loss 0.1998766015233576 | Test Loss 0.19976438090535595
Epoch 420 | Train Loss 0.1998253346408226 | Test Loss 0.1997106311629599
Epoch 440 | Train Loss 0.19978534191738714 | Test Loss 0.1996683591889015
Epoch 460 | Train Loss 0.1997541440118482 | Test Loss 0.19963508205122227
Epoch 480 | Train Loss 0.1997298068370851 | Test Loss 0.1996088577143953
Epoch 500 | Train Loss 0.1997108216421471 | Test Loss 0.19958816677656194
Epoch 520 | Train Loss 0.19969601147085964 | Test Loss 0.1995718201105018
Epoch 540 | Train Loss 0.19968445819392444 | Test Loss 0.19955888672994096
Epoch 560 | Train Loss 0.1996754455888482 | Test Loss 0.19954863744799745
Epoch 580 | Train Loss 0.19966841493791576 | Test Loss 0.19954050086661804
Epoch 600 | Train Loss 0.1996629303909952 | Test Loss 0.19953402899473288
Epoch 620 | Train Loss 0.19965865194559942 | Test Loss 0.19952887038533382
Epoch 640 | Train Loss 0.1996553143689939 | Test Loss 0.19952474914424784
Epoch 660 | Train Loss 0.19965271075558552 | Test Loss 0.1995214485245173
Epoch 680 | Train Loss 0.19965067970022277 | Test Loss 0.19951879810224835
Epoch 700 | Train Loss 0.19964909529221977 | Test Loss 0.19951666374991373
Epoch 720 | Train Loss 0.1996478593097941 | Test Loss 0.19951493979494447
Epoch 740 | Train Loss 0.1996468951310223 | Test Loss 0.19951354288561254
Epoch 760 | Train Loss 0.19964614298383382 | Test Loss 0.19951240719094615
Epoch 780 | Train Loss 0.1996455562405756 | Test Loss 0.19951148064319446
Epoch 800 | Train Loss 0.19964509852743548 | Test Loss 0.19951072199519815
Epoch 820 | Train Loss 0.19964474146953 | Test Loss 0.19951009851486687
Epoch 840 | Train Loss 0.19964446293186805 | Test Loss 0.19950958417787876
Epoch 860 | Train Loss 0.19964424564714198 | Test Loss 0.19950915825010257
Epoch 880 | Train Loss 0.19964407614528054 | Test Loss 0.19950880417496833
Epoch 900 | Train Loss 0.1996439439184022 | Test Loss 0.1995085086995379
Epoch 920 | Train Loss 0.19964384076940306 | Test Loss 0.19950826118749637
Epoch 940 | Train Loss 0.19964376030379605 | Test Loss 0.19950805307858338
Epoch 960 | Train Loss 0.19964369753329944 | Test Loss 0.19950787746281118
Epoch 980 | Train Loss 0.19964364856659927 | Test Loss 0.19950772874470826

可视化损失函数：