汉森(1982)提出的广义矩估计法
汉森(1982)提出的广义矩估计法(Generalized Method of Moments, GMM)是计量经济学中最重要的参数估计方法之一。以下是对这一经典方法的详细介绍:
一、基本概念
GMM是一种基于矩条件的半参数估计方法,适用于模型设定不完全但能确定一组矩条件的情形。其核心思想是通过使样本矩尽可能接近理论矩来估计参数。
二、模型设定
考虑以下矩条件模型:
E[g(xi,θ0)]=0 E[g(x_i,\theta_0)] = 0 E[g(xi,θ0)]=0
其中:
- g(xi,θ)g(x_i,\theta)g(xi,θ)是qqq维矩函数
- θ0\theta_0θ0是ppp维待估参数
- 当q>pq>pq>p时为过度识别情形
三、估计步骤
-
目标函数构建:
Qn(θ)=[1n∑i=1ng(xi,θ)]′Wn[1n∑i=1ng(xi,θ)] Q_n(\theta) = \left[\frac{1}{n}\sum_{i=1}^n g(x_i,\theta)\right]' W_n \left[\frac{1}{n}\sum_{i=1}^n g(x_i,\theta)\right] Qn(θ)=[n1i=1∑ng(xi,θ)]′Wn[n1i=1∑ng(xi,θ)]
其中WnW_nWn是正定权重矩阵 -
参数估计:
θ^=argminθQn(θ) \hat{\theta} = \arg\min_{\theta} Q_n(\theta) θ^=argθminQn(θ)
四、最优权重选择
汉森证明了当权重矩阵取为:
Wnopt=[1n∑i=1ng(xi,θ~)g(xi,θ~)′]−1 W_n^{opt} = \left[\frac{1}{n}\sum_{i=1}^n g(x_i,\tilde{\theta})g(x_i,\tilde{\theta})'\right]^{-1} Wnopt=[n1i=1∑ng(xi,θ~)g(xi,θ~)′]−1
时(其中θ~\tilde{\theta}θ~为初始一致估计量),GMM估计量达到渐进有效。
五、主要特性
- 一致性:在正则条件下,θ^→pθ0\hat{\theta} \xrightarrow{p} \theta_0θ^pθ0
- 渐进正态性:n(θ^−θ0)→dN(0,V)\sqrt{n}(\hat{\theta}-\theta_0) \xrightarrow{d} N(0,V)n(θ^−θ0)dN(0,V)
- 有效性:最优GMM估计量的方差达到下界
六、应用领域
该方法广泛应用于:
- 工具变量回归
- 资产定价模型
- 动态面板数据模型
- 结构计量模型
七、与SGMM的区别
如文档所述,传统GMM是"离线"方法,需要完整数据集;而SGMM通过随机近似实现了:
- 在线流式处理能力
- 更低的内存需求
- 更快的计算速度
- 保持与传统GMM相同的渐进性质
文中表1和表2的模拟结果验证了SGMM与传统GMM在估计精度上的可比性:
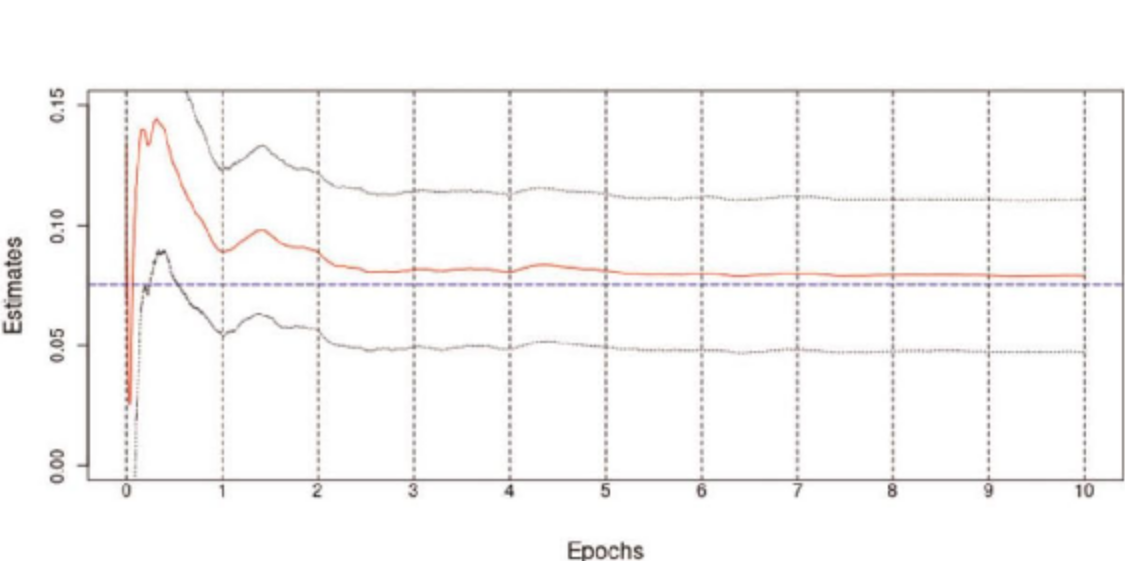
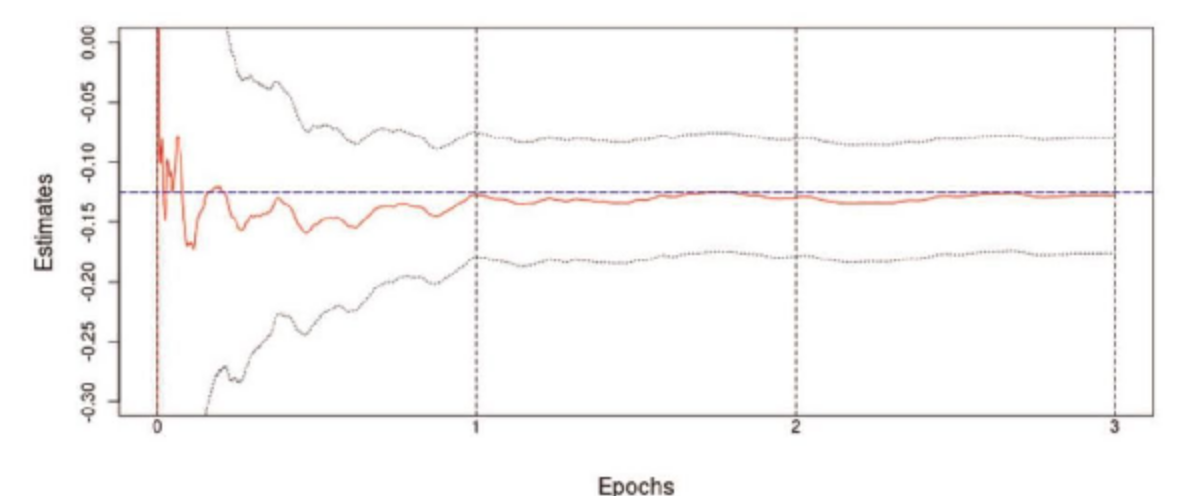
这些结果展示了SGMM在保持统计性质的同时,显著提升了计算效率。
