当前位置：首页 > news >正文

【排序算法】④堆排序

news 2025/8/10 13:25:08

系列文章目录

第一篇：【排序算法】①直接插入排序-CSDN博客

第二篇：【排序算法】②希尔排序-CSDN博客

第三篇：【排序算法】③直接选择排序-CSDN博客

第四篇：【排序算法】④堆排序-CSDN博客

目录

系列文章目录

前言

一、堆是什么？

二、实现堆排序

1.堆排序所需要的堆函数

HeapCreate：堆的构建

核心算法BigADjustUp：(大堆)向上调整算法

HeapPopBig：删除节点

核心算法BigADjustDown：向下调整算法

HeapDestory：堆的销毁

2.堆排序代码

三、分析堆排序

总结

前言

堆排序是指利用二叉树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。

值得注意的是：排升序要建大堆，排降序建小堆。

一、堆是什么？

想要了解堆是什么，首先需要明白什么是完全二叉树

完全二叉树：

1. 二叉树：由一个根节点加上两棵别称为左子树和右子树的二叉树组成。

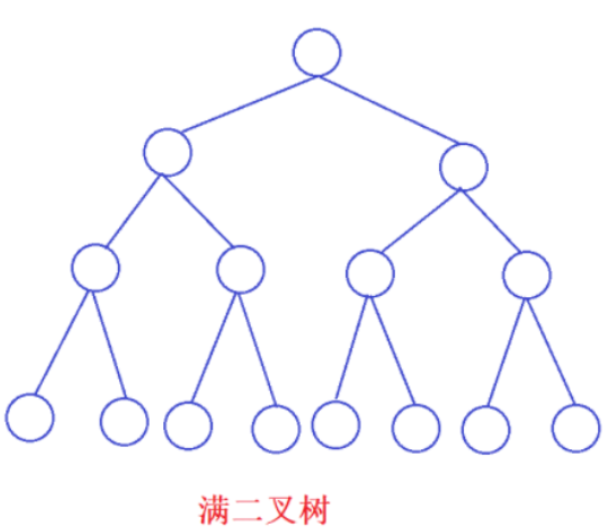
2. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
3. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

堆的定义：

如果有一个码的集合K = {k0 ，k1 ，k2 ，…，kn-1 }，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：ki <= k2i+1且ki <= k2i+2( ki>=k2i+1 且ki >=k2i+2 ) i = 0，1，2…，则称为小堆(或大堆).

简单来说：

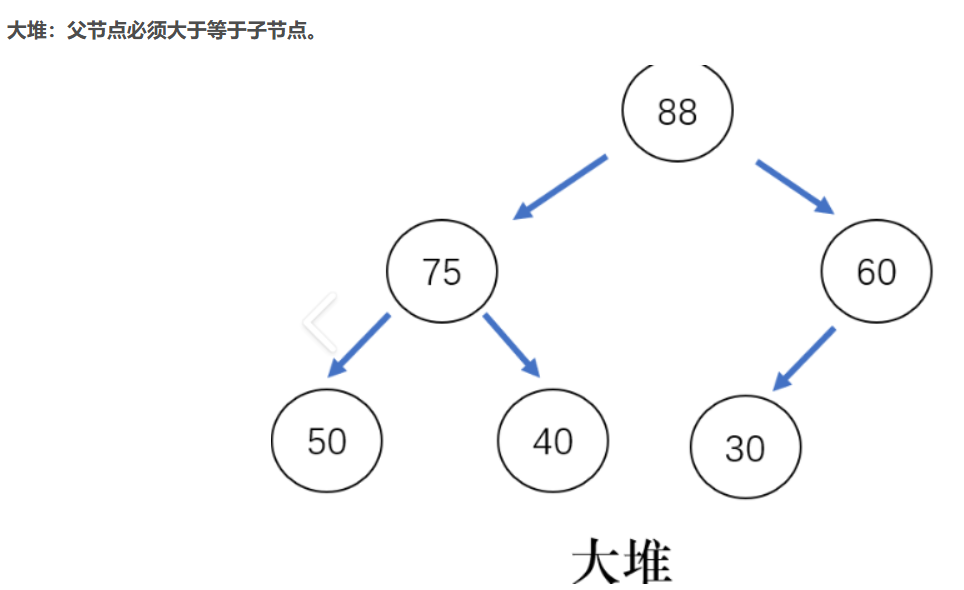
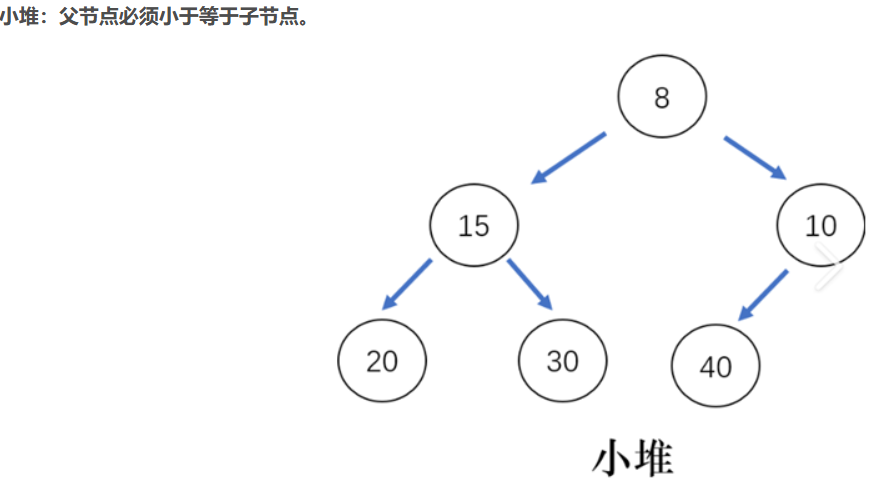
完全二叉树由于其性质非常适合使用顺序结构存储，所以，现实中我们通常把堆使用顺序结构的数组来存储。

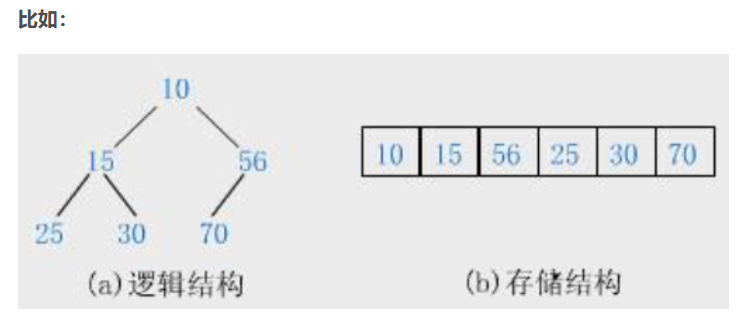
于是我们可以推出堆的数据结构：

typedef int HPDataType;typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;

上面是简述堆的概念，目的是为堆排序准备。若是之前未接触过堆这种数据结构的读者，强烈建议先看看链接文章：【数据结构】二叉树①-堆-CSDN博客

二、实现堆排序

本文以外部建堆实现堆排升序为例进行介绍，至于本地建堆或者堆排降序由于核心思想未变，可同理得出。

1.堆排序所需要的堆函数

HeapCreate：堆的构建

通过传入数组a和数据个数nums，直接将传入的数组构造成小堆。

// 堆的初始化，并构建传入数组：为堆排序
void HeapCreateBig(Heap* hp, HPDataType* a, int nums)
{if(!hp||!a)return;HPDataType* temp = (HPDataType*)malloc(sizeof(HPDataType) * nums);if (temp){hp->_a = temp;hp->_capacity = nums;hp->_size = nums;}else{perror("HeapCreate malloc fail");exit(-1);}for (int i = 0; i < nums; ++i){hp->_a[i] = a[i];BigADjustUp(hp, i);}
}

上述代码的核心在于最后的for循环：

①在循环中，将外部a数组的数据一个一个赋予给malloc出来堆中的数组；

②每赋予一个值，便调用依次BigADjustUp函数。

核心算法BigADjustUp：(大堆)向上调整算法

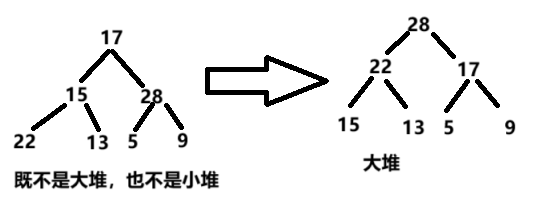
假设有一个数组，在逻辑上看做一颗完全二叉树。我们通过从根节点开始的向上调整算法可以把它调整成一个大堆。

假设该数组为：

int a[] = { 17,15,28,22,13,5,9 };

可以看到该数组中的内容并不符合大堆要求。

向上调整算法核心思路：

①默认数组第一个元素为根节点数据；

②之后每Push进一个数据，便与它的父节点比较，若父节点数据小于子节点数据，则交换，然后将父节点(下标)赋值给子节点，再计算新父节点，重复上述步骤，直至子节点到根结点处（下标为0时）。

③中途若父节点数据大于等于子节点数据（满足小堆要求），则break跳出循环。

代码参考：

//大堆调整：
void BigADjustUp(Heap* hp, int loc)
{assert(hp);HPDataType* a = hp->_a;int child = loc;int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child]){swap(&a[parent], &a[child]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

解释：

①父节点（parent）、子节点（child）在代码中表示的是数组下标；

②loc，即location位置的意思，记录Push数据在数组中的下标；

③计算新父节点：（左孩子或者右孩子的下标-1）/ 2就==他们父节点的下标，比如数组下标1与数组下标2的父节点在数组中就是下标0；

④每push进一个数据，先让他做当前位置对应的左或者右孩子（该位置肯定是是叶节点），然后通过向上调整算法，若数据大于父节点中的数据，则交换、上升。

用该算法调整后：

int a[] = { 17，15，28，22，13，5，9 };

调整后：{28，22，17，15，13，5 ，9}；

HeapPopBig：删除节点

将堆顶元素与数组最后一个元素交换，_size--，然后调用向下调整算法。

// 堆的删除:为堆排序
void HeapPopBig(Heap* hp)
{assert(hp);assert(hp->_a);swap(&hp->_a[0], &hp->_a[hp->_size - 1]);hp->_size--;BigADjustDown(hp, 0);
}

将堆顶元素与最后一个元素交换位置后，重要的是调用BigADjustDown（）函数，使得堆能继续成立。

核心算法BigADjustDown：向下调整算法

向下调整算法有一个前提：左右子树必须是堆，才能调整。

堆的删除，即删除堆顶元素需要用到第二个核心算法——向下调整算法。

我们先说明堆删除的思想：将堆顶元素与数组最后一个元素交换，然后_size--。

也就是说，向下调整算法的核心目标是：将堆顶所在的元素调整到适合它的位置。

算法思路：

①选择该父节点对应的左/右孩子节中值较大的那一个，与父节点的值交换（一开始是根节点）；

②将交换的孩子节点当作新一轮的父节点，重复①；

③直到数组末尾，或者中途遇到小于或等于，满足小堆条件退出。

void BigADjustDown(Heap* hp, int loc)
{assert(hp);HPDataType* a = hp->_a;//parent与child均为下标int parent = loc;int lchild = parent * 2 + 1, rchild = (parent + 1) * 2, max_child = 0;while (parent < hp->_size){max_child = a[lchild] > a[rchild] ? lchild : rchild;if (hp->_a[max_child] > hp->_a[parent] && max_child < hp->_size){swap(&hp->_a[parent], &hp->_a[max_child]);parent = max_child;lchild = parent * 2 + 1;rchild = (parent + 1) * 2;}else{break;}}}

解释：

①新父节点下标：已知父节点的数组下标，那么该节点的左孩子数组下标=父节点下标*2+1，右孩子数组下标=（父节点下标+1）*2。如父节点数组下标为0，则左孩子为0*2+1，右孩子为（0+1)*2。

②BigADjustDown是配合HeapPopBig使用的，所以不要忘了实际场景是：堆顶与末尾数据进行了交换，需要BigADjustDown重新调整堆。

这也是为什么排升序要建大堆，排降序建小堆的原因：因为实现机制是将堆顶数据倒插到数组尾，大堆堆顶是数组数据最大的，故为升序；小堆堆顶是数组最小的，故为降序。

HeapDestory：堆的销毁

记得将无用指针置空，防止野指针。

// 堆的销毁
void HeapDestory(Heap* hp)
{assert(hp);free(hp->_a);hp->_capacity = hp->_size = 0;hp->_a = NULL;
}

2.堆排序代码

//堆排序:升序
void HeapSortUp(int* a, int n)
{if (!a)return;Heap he;HeapCreateBig(&he, a, n);int cnt = n;while (cnt){HeapPopBig(&he);cnt--;}for (int i = 0; i < n; ++i)a[i] = he._a[i];HeapDestory(&he);
}

解释：

①将传入的数组通过HeapCreateBig构建起大堆；

②while循环，通过利用HeapPopBig每循环一次将堆顶（最大数据）移动至数组末尾，由于HeapPopBig一次成员变量_size便会--（数组尾下标不断向前），当循环结束后成员变量数组_a存储的数据便是升序排列；

这里利用HeapPopBig删除机制，将堆顶逐渐移动至数组尾，但注意不是真正的删除了而是堆中的_size--了（下次再向堆中push数据就会将原数据覆盖），实际如果不再push那么这些数据是依然存在的。

③最后的for循环将排好的堆内数组挨个赋值给外部数组，之后再销毁堆。

以上述调整后：{28，22，17，15，13，5 ，9}的数组为例模仿代码执行，

while中HeapPopBig执行情况：

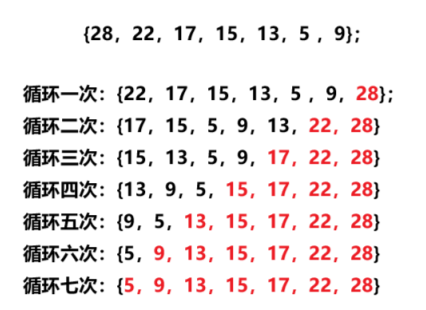
三、分析堆排序

特性总结：
1.同样是选择排序，相比直接选择排序，堆排序使用堆来选数，效率高了很多。
2. 时间复杂度：建堆过程为O(n)，每次调整（弹出）为O(log n)，总共n次调整，所以整体时间复杂度为O(n log n)
3. 空间复杂度：本文中的代码实现为O(N)（也可以采取另一种原地建堆的方法，那样空间复杂度为O(1)）；
4. 稳定性：不稳定，交换堆顶和末尾元素时，可能破坏相同元素的相对顺序。