【DFS系列 | 递归】DFS算法入门：递归原理与实现详解

算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！

深度优先搜索（DFS）是算法学习中的重要基石，而递归则是实现DFS最直观的方式。但对于初学者来说，递归的执行流程、函数调用栈以及搜索终止条件往往令人困惑。本文将从递归的基本原理出发，结合DFS的遍历过程，详细解析递归调用的执行机制、DFS的核心思想，并通过经典问题（如二叉树遍历、图的连通性检测等）演示如何用代码实现DFS算法，帮助读者真正掌握这一基础而强大的搜索策略。

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏： 初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志 我自踏雪至山巅

前言：名词解释(入坑必看)

一、递归

1.什么是递归

递归是指函数自己调用自己的情况，通常二叉树、快排、归并都有递归的影子

2.为什么会用到递归

将大问题分解无数的小问题，大事化小。

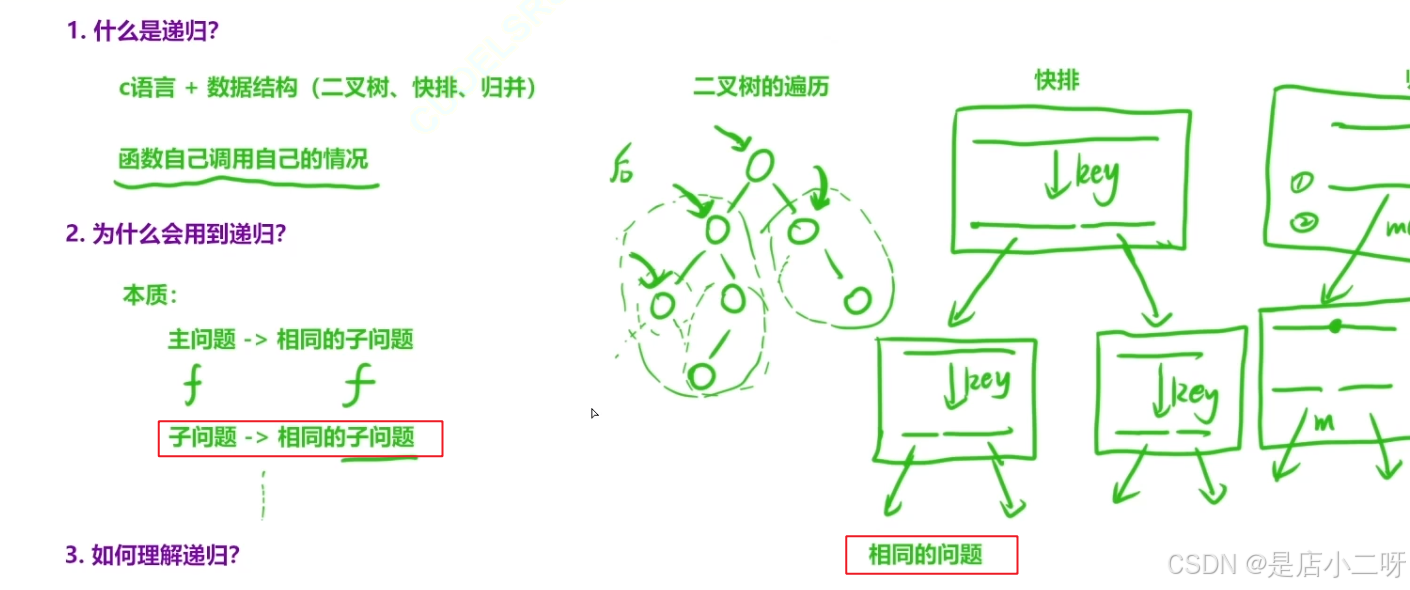
3.如何理解递归

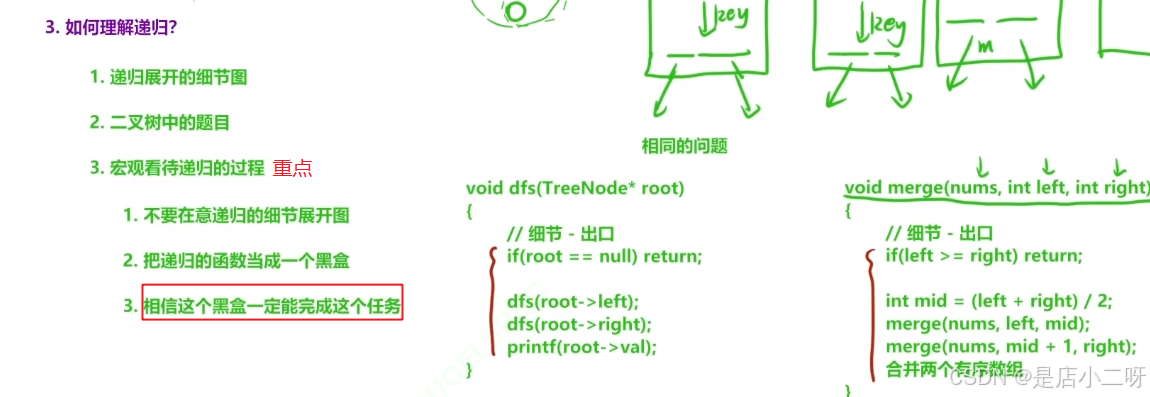
4.如何写好递归的步骤

二、搜索 vs 深度优先遍历 vs 深度优先搜索 vs 宽度优先遍历的vs 宽度优先搜索 vs 暴搜

理解：遍历是形式、目的是搜索

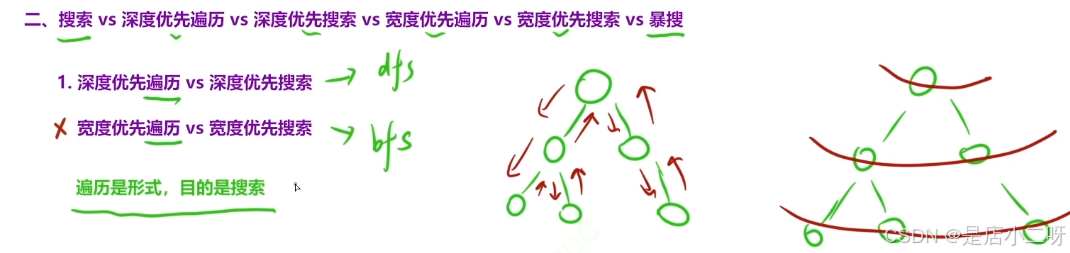
三、回溯与剪枝

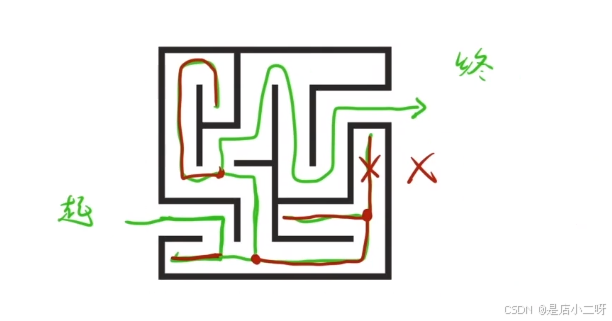
• 回溯是一种算法思想，它通过一步步尝试不同的选择来寻找问题的解。如果发现某一步无法继续，就回到上一步再尝试其他可能性。
• 剪枝是回溯过程中的优化技术，它通过提前判断哪些路径不可能得到解，避免不必要的计算，从而提高效率。

就像在迷宫中找路，回溯是你走到一个岔路口时，选择一条路试试看，如果走不通就退回去重新选择；剪枝是你在走之前就判断哪些路根本没可能到达终点，直接不走那些路。

---

面试题 08.06. 汉诺塔问题

【题目】：面试题 08.06. 汉诺塔问题

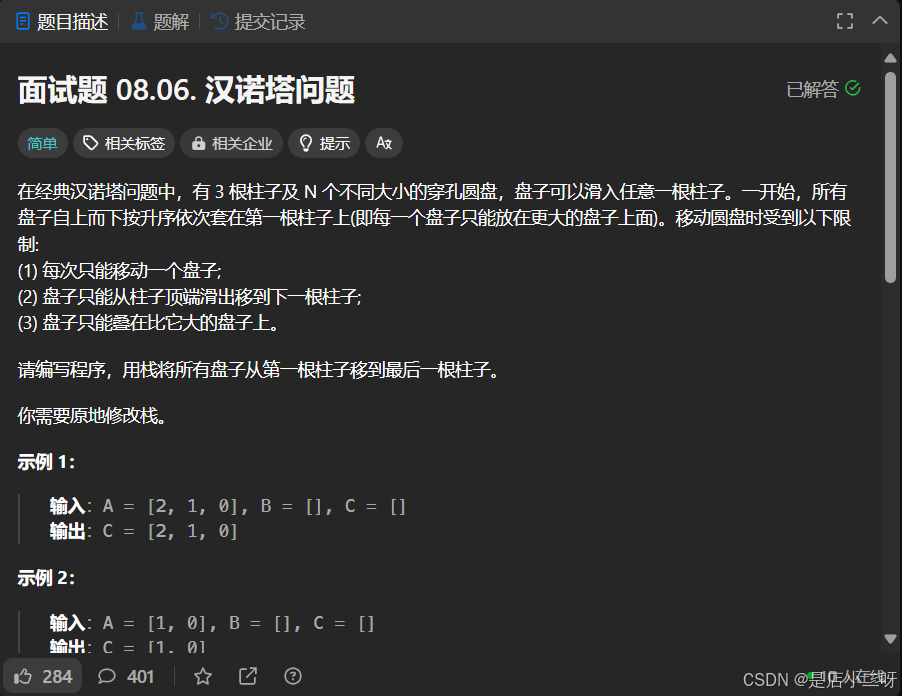
【算法思路】

【1.如何解决汉诺塔问题】

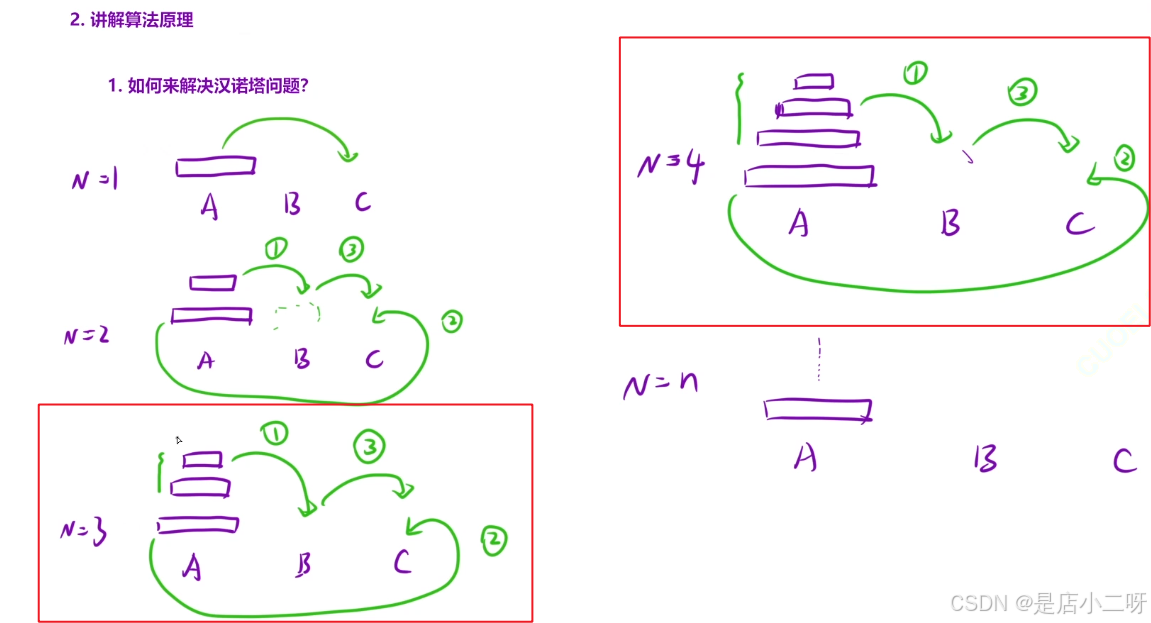
【2.为什么可以用递归】

• 大问题->相同类型的子问题
• 子问题->相同类型的子问题

通过绘图可以看出，求解N = n的问题和求解N = n - 1的问题本质上是相同类型的子问题。因此，基于上述三步法，我们可以理解如何编写递归代码。

【3.如何编写递归的代码】

将递归函数看出一个黑箱，相信黑盒可以帮助我们完成任务。

1..重复子问题:设计函数头

该Dfs函数 能将x柱子上的一堆盘子，借助y柱子，转移到z柱子上面，故而void dfs(x, y , z, int n)。

2..只关心某一个子问题在做什么->函数体

• 【第一步】:将x柱子上的n - 1个盘子，借助z柱子，转移到y柱子上
• 【第二步】:将x柱子剩下盘子，转移到z柱子上
• 【第三步】:最后将y柱子上 n - 1个盘子，借助x柱子，转移到z柱子上

通过子问题的解决方案，去解决类似子问题，从而解决大问题。

3.递归出口

当递归到达最后一次，需要设计出口返回。这里就是N = 1，x.back()转移到柱子上

【代码实现】

class Solution {
public:void hanota(vector<int>& a, vector<int>& b, vector<int>& c) {dfs(a, b, c, a.size());}void dfs(vector<int>& a, vector<int>& b, vector<int>& c, int n){if(n == 1){c.push_back(a.back());a.pop_back();return ;}dfs(a, c, b, n - 1);c.push_back(a.back());a.pop_back();dfs(b, a, c, n - 1);}
};

---

21.合并两个有序链表

【题目】：21. 合并两个有序链表

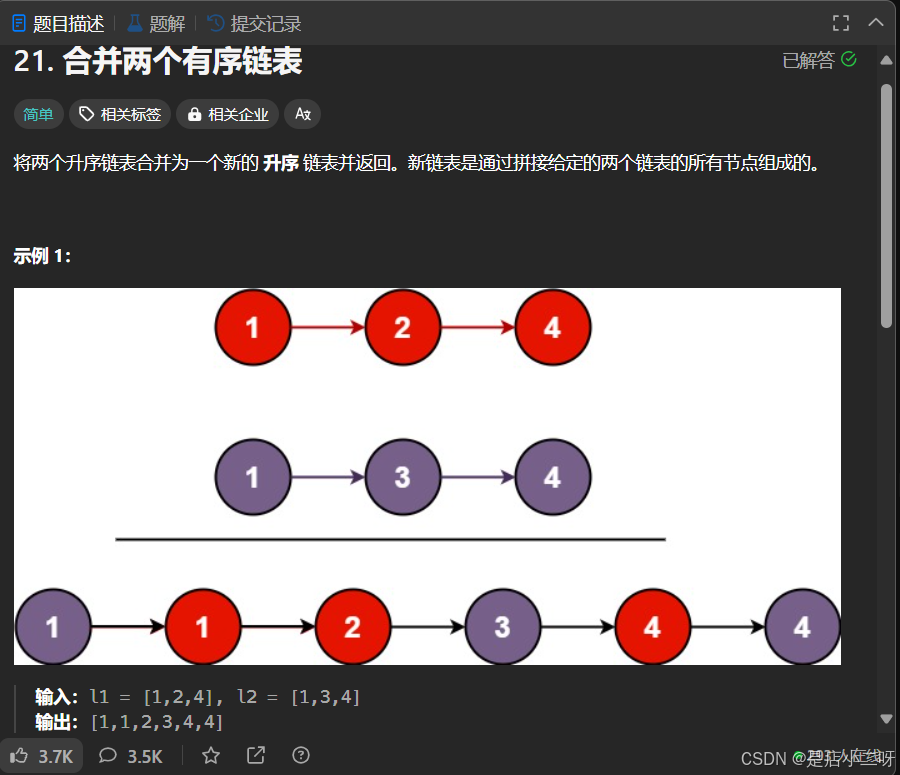
【算法思路】

当出现重复的子问题时，可以考虑使用递归问题。我们需要判断重复子问题 + 宏观看待递归问题

1. 重复子问题->函数头的设计

这里的重复子问题是‘合并两个有序链表’，在解决数据结构相关问题时，建议通过绘图来分析问题。通过绘制，可以发现函数的返回值应该是一个 Node* 指针，函数接受两个链表的指针作为参数，功能是‘返回合并后有序链表的头节点’。

2. 只关心某一个子问题在做什么事情->函数体的设计

【第一步】:比较大小，用较小节点去连接"合并两个有序链表"返回的头节点

【第二步】:接收链表l1 -> next = dfs(l1->next, l2)，这里展示 l1-val < l2->val情况，l2同理可得。

3. 递归出口

如果链表1为空，返回链表2；如果链表2为空，返回链表1；如果两个链表都为空，则返回顺便一个链表指针。

【代码实现】

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2){if(list1 == nullptr) return list2;if(list2 == nullptr) return list1;if(list1->val <= list2->val){list1->next = mergeTwoLists(list1->next, list2);return list1;}else{list2->next = mergeTwoLists(list1, list2->next);return list2;}}
};

循环(迭代) vs 递归

---

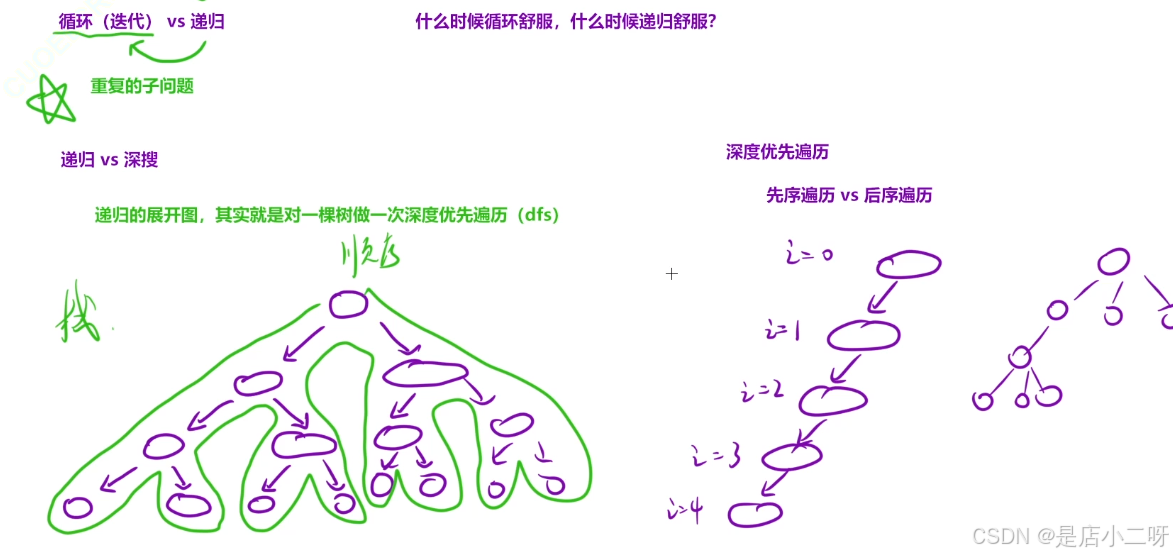
206.反转链表

【题目】：206. 反转链表

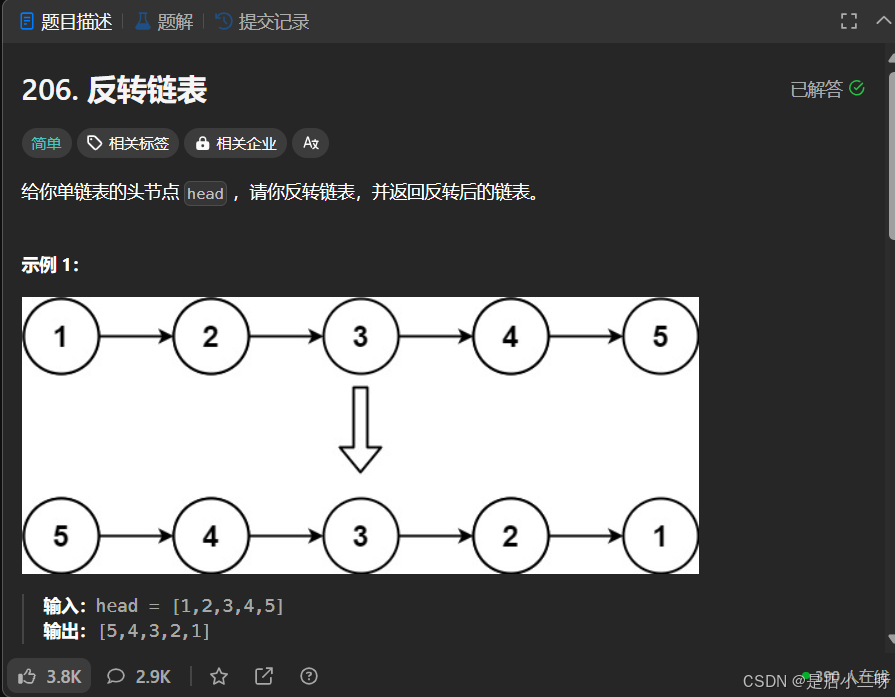
【算法思路】

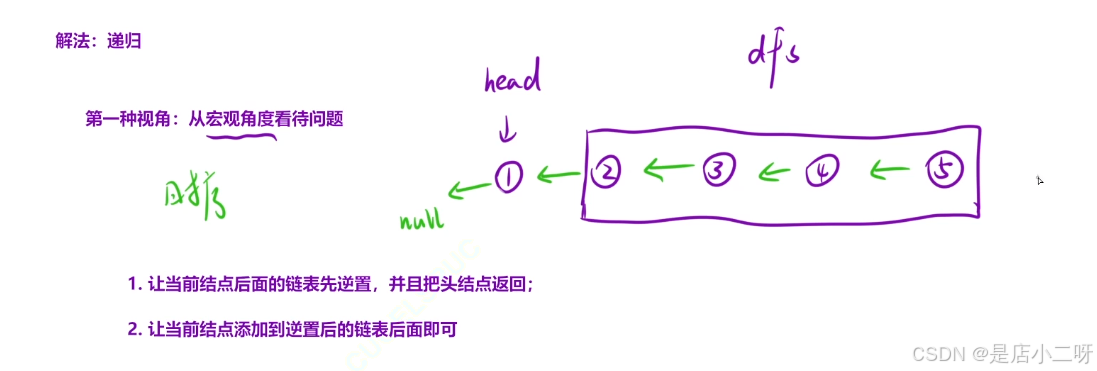
【函数头】:功能设计为"当前节点后面的链表逆序，然后返回逆序后指针"

【函数体】:让当前节点后面的链表先逆置，并且把头节点返回；让当前节点添加到逆着后的链表后面即可。

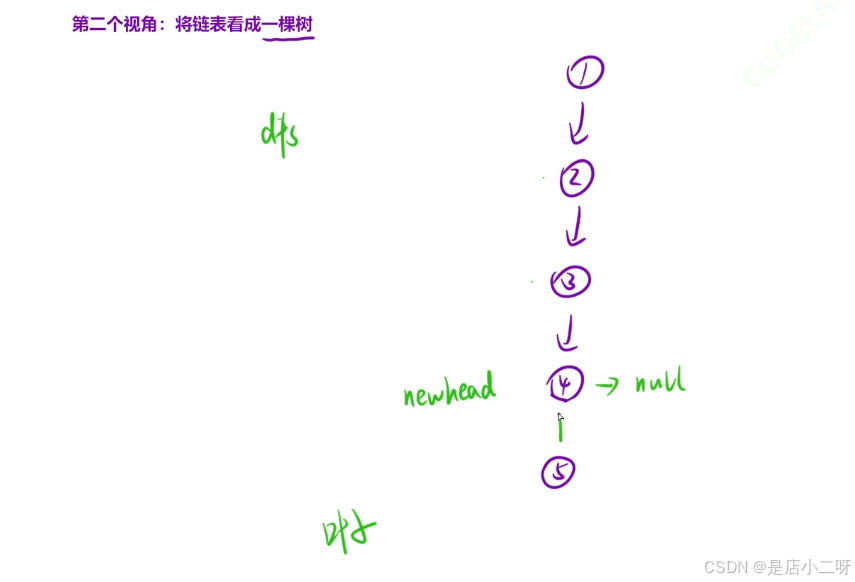
【代码实现】

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution 
{
public:ListNode* reverseList(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode * newHead = reverseList(head-> next);head->next->next = head;head->next = nullptr; return newHead;}
};

【个人思考】

在处理链表相关问题，特别是链表指向关系时，一定要画图分析，否则很难理解像 head->next->next = head; 这样的表达式的含义。

---

24.两两交换链表中的节点

【题目】：24. 两两交换链表中的节点

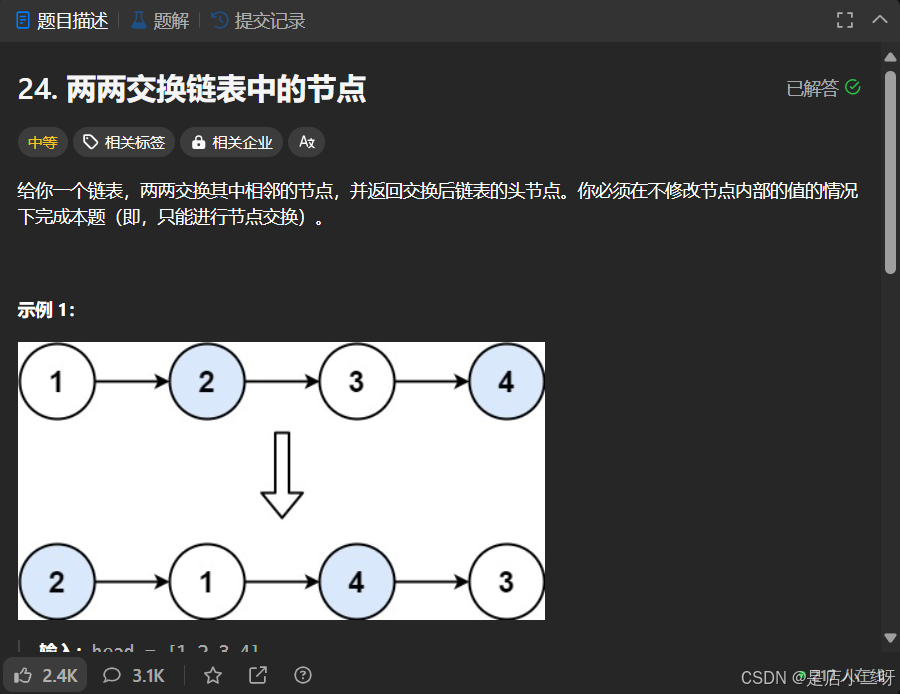
【算法思路】

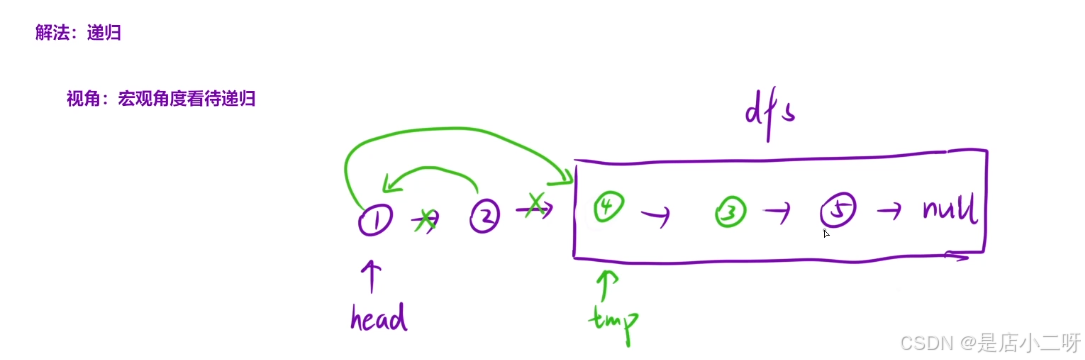
【函数头】:功能设计为"将后续节点两两交换，返回链表指针"，也是属于相关类型子问题。

【函数体】:使用tmp变量接收后续"节点两两交换"链表指针，按照图中连接方式，进行调动。

【代码实现】

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode() : val(0), next(nullptr) {}*     ListNode(int x) : val(x), next(nullptr) {}*     ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode * tmp = swapPairs(head->next->next);ListNode * ret = head->next;head->next->next = head;head->next = tmp;return ret;}
};

---

50. Pow(x, n)

【题目】：50. Pow(x, n)

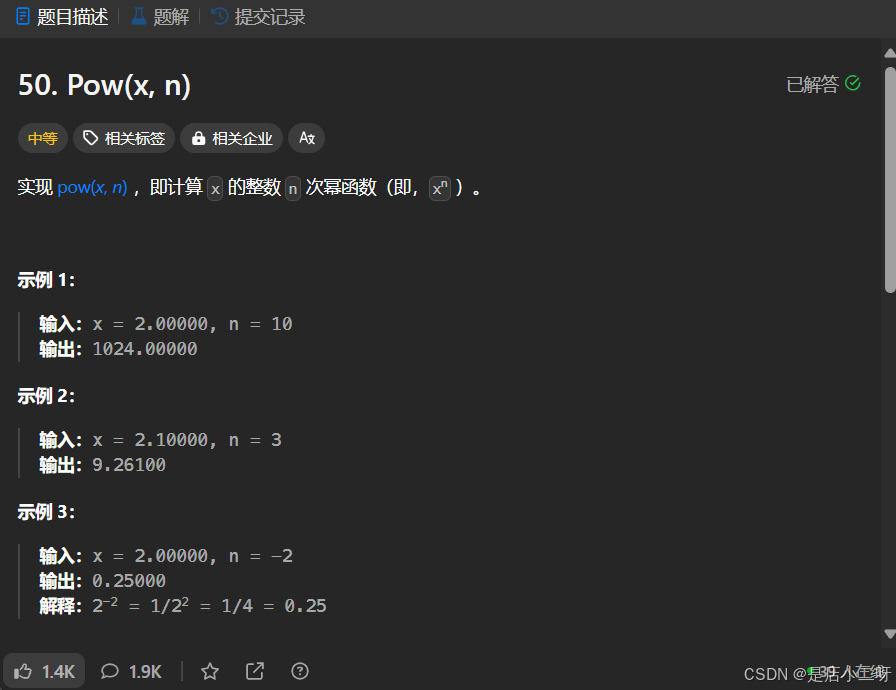
【算法思路】

1.相同子问题->函数头设计

通过利用指数幂的性质，将问题转化为相关的子问题，函数为 int pow(x, n)。

2.只关心每一个子问题做了什么->函数体

【代码实现】

class Solution {
public:double myPow(double x, int n) {return n < 0 ? 1.0 / pow(x, -(long long)n) :pow(x,n);}double pow(double x, long long n) {if(n == 0) return 1.0;double tmp = pow(x, n/2);return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;}
};

【细节问题】

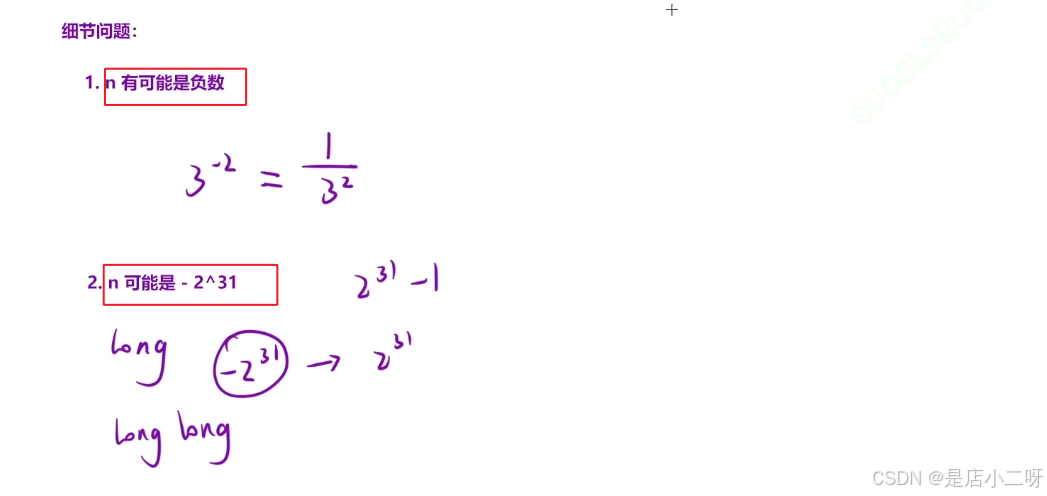
快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！