优选算法2

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

7. 分治-快排

就是把一个大问题划分为子问题，在把子问题划分为更小的子问题

7.1 颜⾊分类

颜⾊分类

数组分三块

以前的移动零，划分为两个区域，所以就是双指针

这个就相当于把小于1的放左边，大于1的放右边，等于1的放中间
划分三个区域，可以搞一个三指针

i来遍历，left指向0的最右侧，指向的就是0，right指向2的最左侧，指向的就是2

0~left:全是0
left+1~i-1：全是1
i~right-1：未扫描
right~n-1：全是2

nums[i]
为0时：交换left+1和i，i++，left++
为1时，i++
为2时：交换right-1，与i，i不变，right–


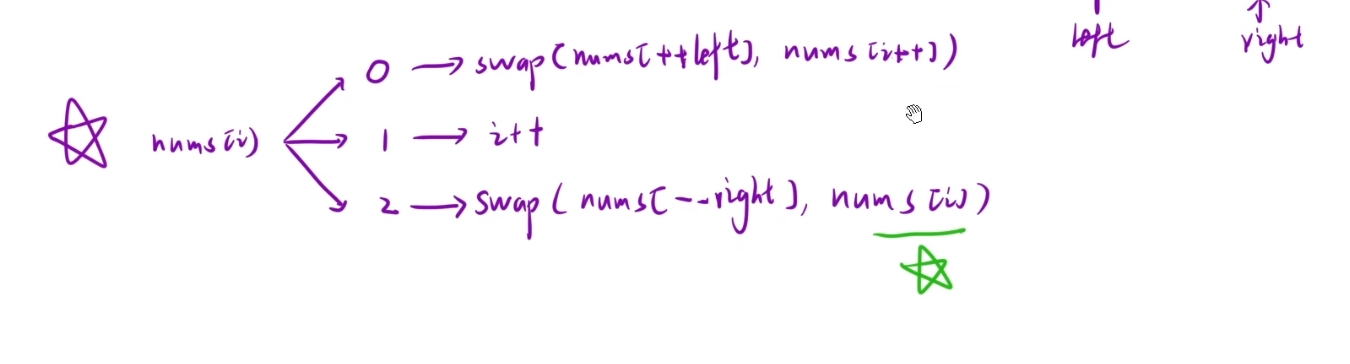
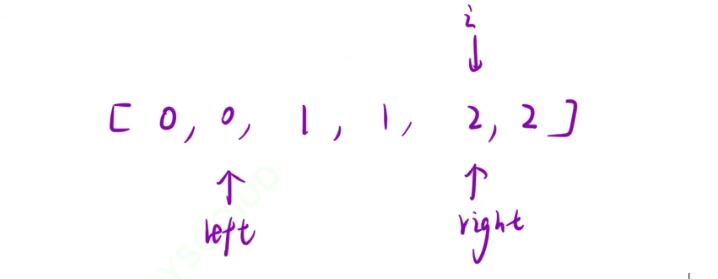
初始化：left=-1,right=n

class Solution {void swap(int[] nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;}public void sortColors(int[] nums) {int left = -1 , right = nums.length , i =0;while(i<right){if(nums[i]==1){i++;}else if(nums[i]==0){swap(nums,i,left+1);left++;i++;}else if(nums[i]==2){swap(nums,i,right-1);right--;}}}
}

7.2 快速排序

快速排序

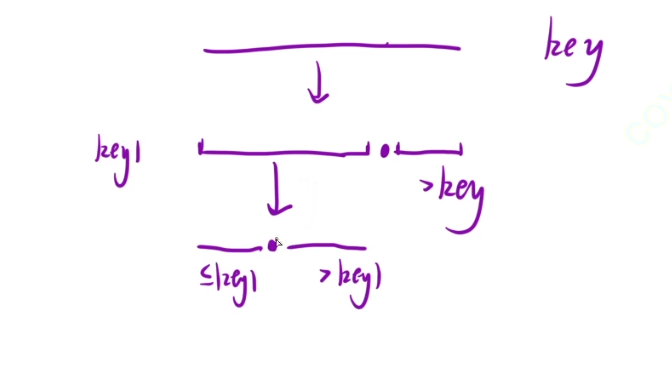
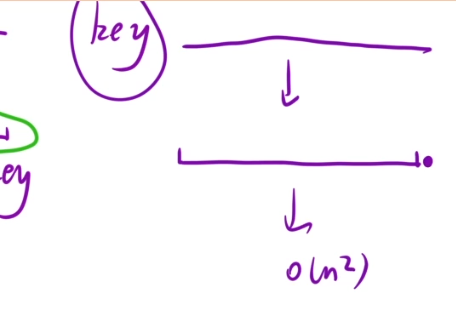
但是如果数据都一样的话，那么就是n^2的复杂度

我们可以分为三个区域
一个小于，一个等于key，一个大于key

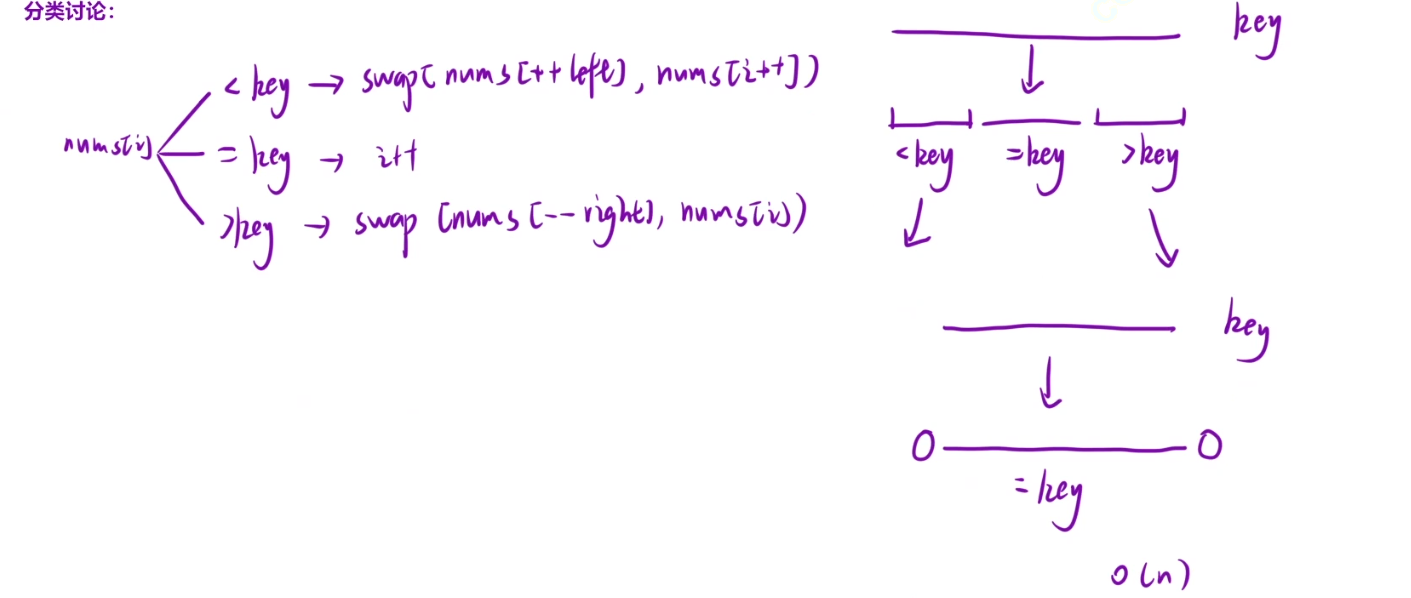
优化选择基准元素：随机选择基准元素：随机数

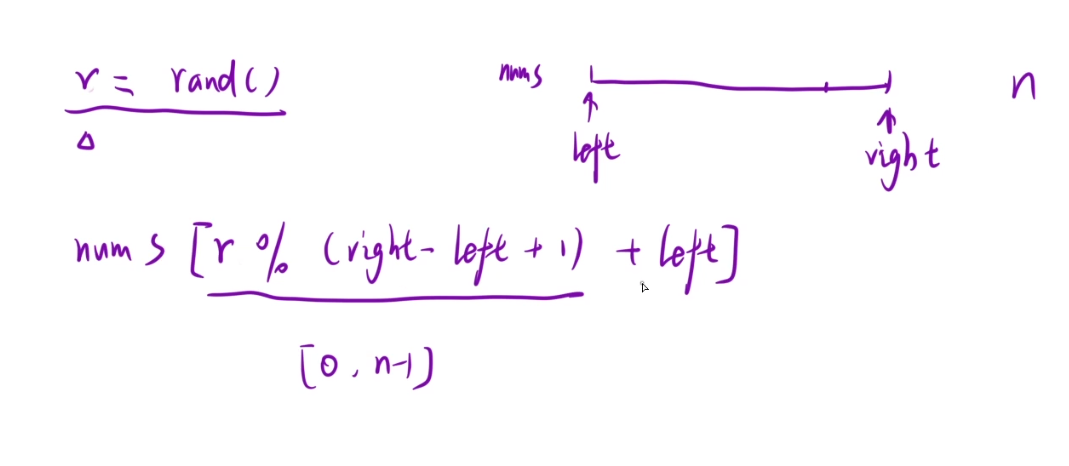
坐标随机生成就可以了

class Solution {public int[] sortArray(int[] nums) {qsort(nums,0,nums.length-1);return nums;}public void qsort(int[] nums,int l,int r){if(l>=r)return ;int left  = l-1 ,right = r+1,i=l;int key = nums[new Random().nextInt(r-l+1) + l];while(i<right){if(nums[i]<key){swap(nums,++left,i++);}else if(nums[i]==key){i++;}else{swap(nums,--right,i);}}qsort(nums,l,left);qsort(nums,right,r);}void swap(int[]nums,int i,int j){int tmp = nums[i];nums[i]=nums[j];nums[j]=tmp;}}

7.3 快速选择算法

快速选择算法

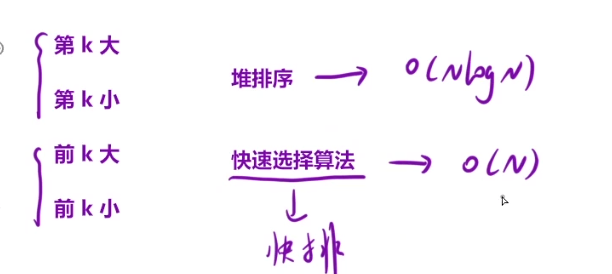
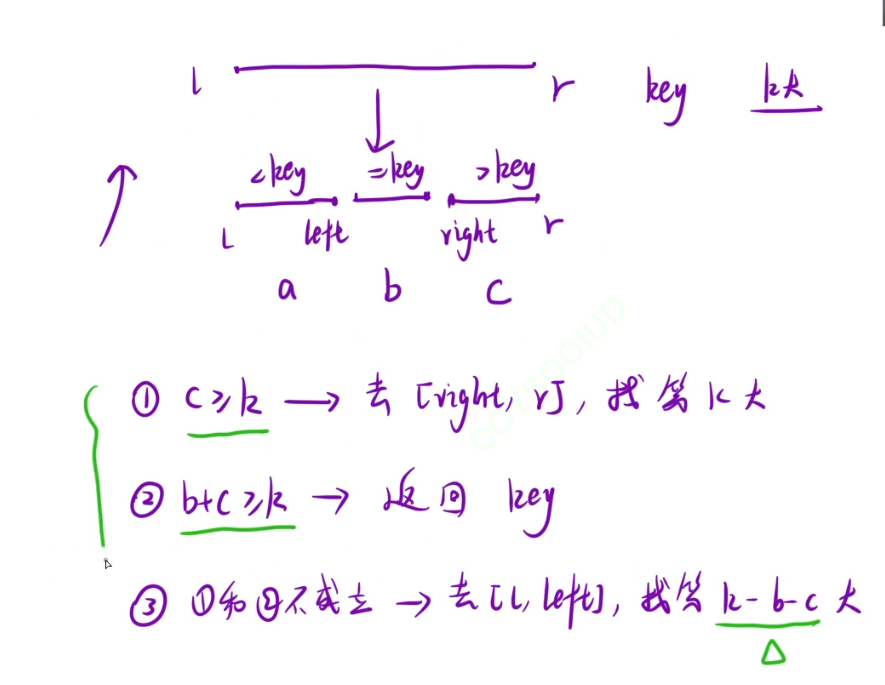
a,b,c是三个区间的元素个数

就是对数组进行快速排序，然后一次快速排序的结果进行处理，看三个区间的长度，如果第三个区间长度大于k，说明第k大的就在第三个区间
如果第二和第三区间大于k，说明第三个区间小于k，第k大肯定不在第三区间，而第二和第三区间大于k，说明第k大就在这两个区间，所以就在第二个区间
当然整个区间长度肯定大于k，上面两个都不满足，说明第k大肯定在第一区间，所以就在第一区间找k-b-c大的

class Solution {public int findKthLargest(int[] nums, int k) {return sort(nums, 0, nums.length-1,k);}public int sort(int[]nums ,int l,int r ,int k){int key  = nums[new Random().nextInt(r-l+1)+l];int left = l-1,right = r+1,i=l;//快速排序while(i<right){if(nums[i]<key) swap(nums,i++,++left);else if(nums[i]==key)i++;else swap(nums,i,--right);}//三个区间，，，，l,left   left+1,right-1  right,rint b = right-left-1,c = r-right+1;if(c>=k)return sort(nums,right,r,k);else if((b+c)>=k)return nums[right-1];else  return sort(nums,l,left,k-b-c);}void swap(int[]nums,int i,int j){int tmp = nums[i];nums[i]=nums[j];nums[j]=tmp;}
}

7.4 最⼩的 k 个数

最⼩的 k 个数

第一可以创建一个大根堆
第二就是排序
第三就是快速选择算法

就是三个区间中找左边的数据
区间长度分别为a,b,c
a>k:最小的k个在第一个区间
a+b>=k:最小的k个，就是第一个区间，和剩余的k-a个第二个区间里面的东西
前面两个都不满足的话：那么前面两个区间都是最小的，然后在剩下的right,r区间里面找k-a-b个最小的

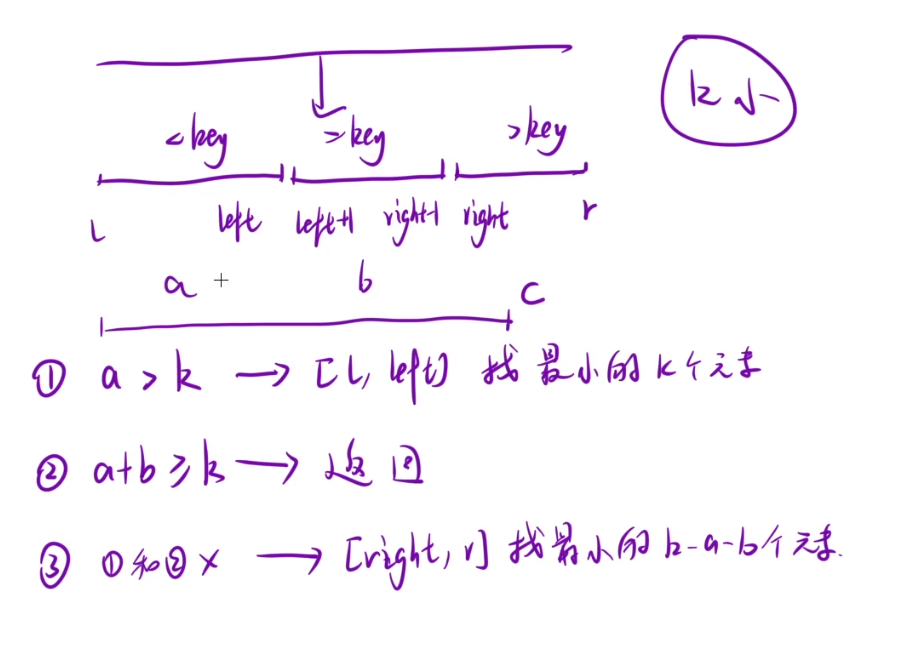
可以把k的大小一直变化，放入图中，就知道为什么这样了,将k的大小长度放入图中进行比较，就一目了然了

class Solution {public int[] inventoryManagement(int[] nums, int k) {qsort(nums,0,nums.length-1,k);//将最小的k个放前面int[] ret = new int[k];for(int i=0;i<k;i++){ret[i] = nums[i];}return ret;}public void qsort(int[]nums , int l,int r,int k){if(l>=r)return;//如果这里不返回的话，当l==r的时候，还会继续执行，然后l就<r了int key = nums[new Random().nextInt(r-l+1) + l];int left = l-1,right = r+1,i=l;while(i<right){if(nums[i]<key) swap(nums,i++,++left);else if(nums[i]==key) i++;else swap(nums,i,--right);}//一次快速排序完成int a = left -l +1;int b = right -left -1;if(a>=k) qsort(nums,l,left,k);else if(a+b>=k) return ;else qsort(nums,right,r,k-a-b);}public void swap(int[]nums,int i,int j){int tmp = nums[i];nums[i]=nums[j];nums[j]=tmp;}
}

8. 分治-归并

8.1 归并排序

归并排序

class Solution {int[]tmp;public int[] sortArray(int[] nums) {tmp= new int[nums.length];mergeSort(nums,0,nums.length-1);return nums;}void mergeSort(int[]nums,int left,int right){if(left>=right){return;}int mid = (left+right)/2;mergeSort(nums,left,mid);mergeSort(nums,mid+1,right);//排序排完了左右区间//合并两个有序数组int i = left ,j = mid+1,x=left;while(i<=mid&&j<=right){tmp[x++] = nums[i]<nums[j]?nums[i++]:nums[j++];}while(i<=mid){tmp[x++]=nums[i++];}while(j<=right){tmp[x++]=nums[j++];}for(int y = left;y<=right;y++){nums[y]=tmp[y];}}
}

8.2 数组中的逆序对

数组中的逆序对

暴力枚举：n^2

可以这样，先在左区间挑选出逆序对，然后是右区间，然后是左右区间一起的逆序对，最后在一起排序
就是相当于左区间选两个，右区间选两个，然后左右区间各选一个，这样就可以了

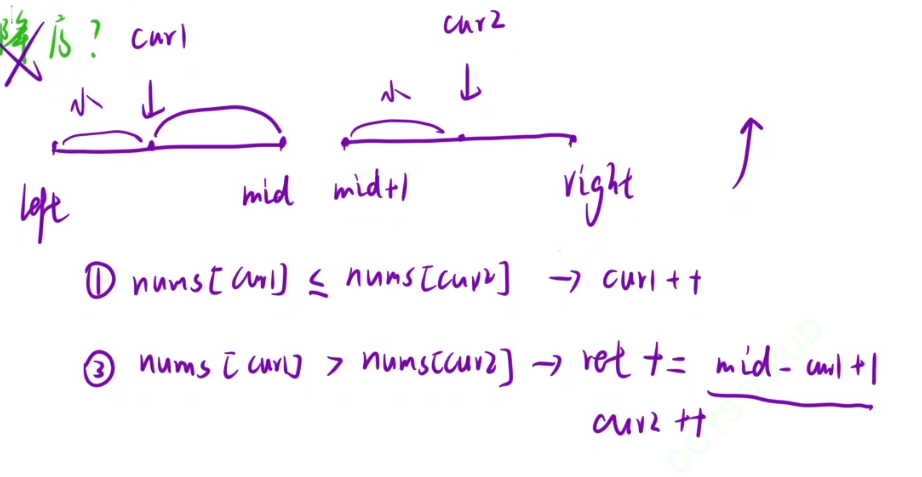
找一个区间的某个数有多少个比它大的时候，可以用升序的归并排序
如果找多少个小的，那么就用降序的归并排序

class Solution {int[]tmp;public int reversePairs(int[] nums) {tmp=new int[nums.length];return mergeSort(nums,0,nums.length-1);}int mergeSort(int[]nums,int left,int right){if(left>=right)return 0;int ret = 0;int mid = (left+right)/2;ret+=mergeSort(nums,left,mid);ret+=mergeSort(nums,mid+1,right);//mergeSort的作用是返回这两个区间的逆序对，然后还要把这两个区间排好序//先求出左右区间一起的逆序对,一边求，一边排序int cur1= left,cur2=mid+1,i=left;while(cur1<=mid&&cur2<=right){//主要是找左边比右边大的if(nums[cur1]>nums[cur2]){tmp[i++]=nums[cur2++];ret+=mid-cur1+1;//那么cur1后面的都比cur2大，所以可以找到很多个cur2为第二个的逆序对}else{tmp[i++]=nums[cur1++];}}while(cur1<=mid){tmp[i++]=nums[cur1++];}while(cur2<=right){tmp[i++]=nums[cur2++];}for(int j=left;j<=right;j++){nums[j]=tmp[j];}return ret;}
}

这个是升序的归并排序
当然也可以弄降序的归并排序

// class Solution {
//     int[]tmp;//     public int reversePairs(int[] nums) {
//         tmp=new int[nums.length];
//         return mergeSort(nums,0,nums.length-1);
//     }//     int mergeSort(int[]nums,int left,int right){
//         if(left>=right)return 0;
//         int ret = 0;
//         int mid = (left+right)/2;
//         ret+=mergeSort(nums,left,mid);
//         ret+=mergeSort(nums,mid+1,right);
//         //mergeSort的作用是返回这两个区间的逆序对，然后还要把这两个区间排好序
//         //先求出左右区间一起的逆序对,一边求，一边排序
//         int cur1= left,cur2=mid+1,i=left;
//         while(cur1<=mid&&cur2<=right){//主要是找左边比右边大的
//             if(nums[cur1]>nums[cur2]){
//                 tmp[i++]=nums[cur2++];
//                 ret+=mid-cur1+1;//那么cur1后面的都比cur2大，所以可以找到很多个cur2为第二个的逆序对
//             }else{
//                 tmp[i++]=nums[cur1++];
//             }
//         }
//         while(cur1<=mid){
//             tmp[i++]=nums[cur1++];
//         }
//         while(cur2<=right){
//             tmp[i++]=nums[cur2++];
//         }
//         for(int j=left;j<=right;j++){
//             nums[j]=tmp[j];
//         }
//         return ret;
//     }
// }class Solution {int[]tmp;public int reversePairs(int[] nums) {tmp=new int[nums.length];return mergeSort(nums,0,nums.length-1);}int mergeSort(int[]nums,int left,int right){if(left>=right)return 0;int ret = 0;int mid = (left+right)/2;ret+=mergeSort(nums,left,mid);ret+=mergeSort(nums,mid+1,right);//mergeSort的作用是返回这两个区间的逆序对，然后还要把这两个区间排好序//先求出左右区间一起的逆序对,一边求，一边排序int cur1= left,cur2=mid+1,i=left;while(cur1<=mid&&cur2<=right){//主要是找左边比右边大的if(nums[cur1]>nums[cur2]){tmp[i++]=nums[cur1++];ret+=right-cur2+1;//那么cur2后面的都比cur1小，所以可以找到很多个cur1为第一个的逆序对}else{tmp[i++]=nums[cur2++];}}while(cur1<=mid){tmp[i++]=nums[cur1++];}while(cur2<=right){tmp[i++]=nums[cur2++];}for(int j=left;j<=right;j++){nums[j]=tmp[j];}return ret;}
}

8.3 计算右侧⼩于当前元素的个数

计算右侧⼩于当前元素的个数

和逆序对是差不多了
找多少个比它小的—》可以用降序的归并排序
先找左边的，在找右边的
最后是一左一右的

但是要返回数组
那么就是数组对应元素+=right-cur2+1
但是这个已经排完序了，不是以前对应的位置了
怎么加呢，怎么找到以前对应下标的位置呢
我们可以设置一个下标数组index，0，1,2，3,4
让这个数组和nums数组一起变化，那么对应的下标也会一起变化了，这样就可以找到了
所以辅助数组tmp也要两个了

class Solution {int ret[];int index[];int indexTmp[];int numsTmp[];public List<Integer> countSmaller(int[] nums) {int n  = nums.length;ret = new int[n];index = new int[n];indexTmp= new int[n];numsTmp = new int[n];for(int i=0;i<n;i++){index[i]=i;//index与nums同步变化，那么nums排序后的数组也可以找到以前的下标了}mergeSort(nums,0,n-1);List<Integer> l = new ArrayList<Integer>();for(int x : ret){l.add(x);}return l;}public void mergeSort(int[] nums ,int left ,int right){if(left>=right)return;int mid = (left+right)/2;mergeSort(nums,left,mid);//排序并找出每个小于元素个数mergeSort(nums,mid+1,right);int cur1 = left , cur2 = mid+1 ,i =left;while(cur1<=mid&&cur2<=right){if(nums[cur1]>nums[cur2]){//说明cur1比cur2后面的都要大。这样就找到了一左一右的时候，比cur1小的了ret[index[cur1]] += (right-cur2+1);numsTmp[i]=nums[cur1];//降序的indexTmp[i++] = index[cur1++];}else{numsTmp[i] = nums[cur2];indexTmp[i++] =index[cur2++];}}while(cur1<=mid){numsTmp[i]=nums[cur1];indexTmp[i++] = index[cur1++];}while(cur2<=right){numsTmp[i] = nums[cur2];indexTmp[i++] =index[cur2++];}for(int j=left;j<=right;j++){index[j] = indexTmp[j];nums[j]=numsTmp[j];}}
}

8.4 翻转对

翻转对
降序
nums[i]>2nums[j]
说明i比j后面的两倍都要大，
但是nums[i]>2nums[j]不能作为条件去排序了
所以ret的计算和排序要分开来

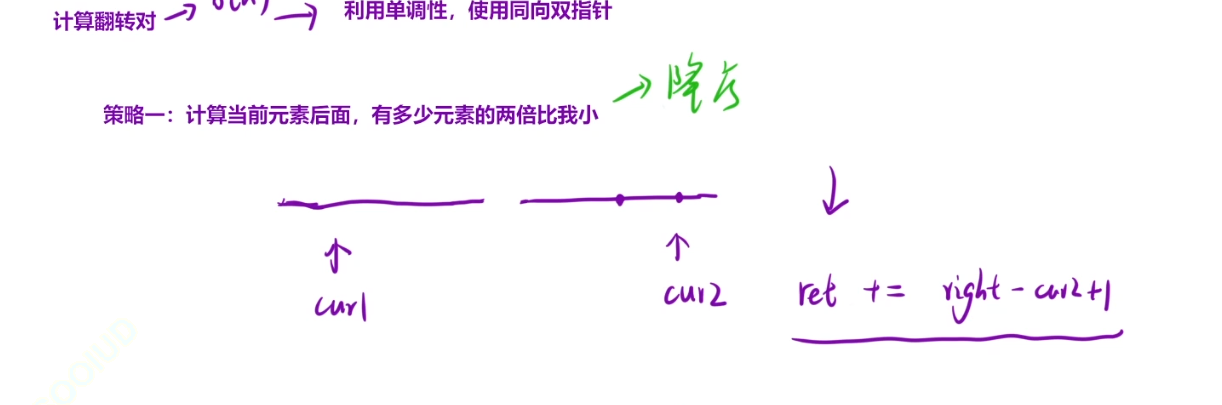
class Solution {int tmp[];public int reversePairs(int[] nums) {tmp = new int[nums.length];return mergeSort(nums,0,nums.length-1);}public int mergeSort(int[]nums,int left ,int right){if(left>=right) return 0;int ret = 0;int mid = (left+right)/2;ret+=mergeSort(nums,left,mid);ret+=mergeSort(nums,mid+1,right);//降序int cur1 = left ,cur2= mid+1,i=left;while(cur1<=mid&&cur2<=right){// if(nums[cur1]>2*nums[cur2]){//不能等于if(nums[cur1]/2.0>nums[cur2]){//防止越界，但是不要/2,要/2.0，这样就可以除的清了，和原来一模一样的意思//cur1肯定也比cur2后面的要大ret+=right-cur2+1;//以cur1开始的翻转对就找完了cur1++;}else{cur2++;}}cur1 = left ;cur2= mid+1;i=left;while(cur1<=mid&&cur2<=right){//现在开始排序tmp[i++] = nums[cur1]>=nums[cur2] ? nums[cur1++]:nums[cur2++];}while(cur1<=mid){tmp[i++] = nums[cur1++];}while(cur2<=right){tmp[i++] = nums[cur2++];}for(int j=left;j<=right;j++){nums[j] = tmp[j];}return ret;}
}

9. 链表

9.1 链表常用技巧和操作总结

第一就是不要吝啬定义变量
第二就是引入虚拟头结点
第三就是注意要判断null
第三就是定义尾指针

9.2 两数相加

两数相加

这个链表是逆序的，刚刚好久满足加法，从低位开始相加

如果不是逆序的，那么就要先逆序

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode addTwoNumbers(ListNode l1, ListNode l2) {ListNode head =new ListNode();//虚拟头结点ListNode cur1 = l1 , cur2 = l2;ListNode tail = head;//指向尾节点int t =0;//记录相加结果while(cur1!=null || cur2!= null || t!=0){if(cur1!=null){t+=cur1.val;cur1 = cur1.next;}if(cur2!=null){t+=cur2.val;cur2 = cur2.next;}ListNode tmp =new ListNode(t%10);tail.next = tmp;tail=tmp;t=t/10;}return head.next;}
}

9.3 两两交换链表中的节点

两两交换链表中的节点

定义一个虚拟头结点的话，就不用单独处理头结点的改变了
然后就是多定义变量就很简单了
因为要涉及四个节点next的指向的变化，所以我们定义四个变量
就是node1~4
node指向newHead，所以下次node1就指向node2了，因为node2和node3已经交换了，可以自己画图试试

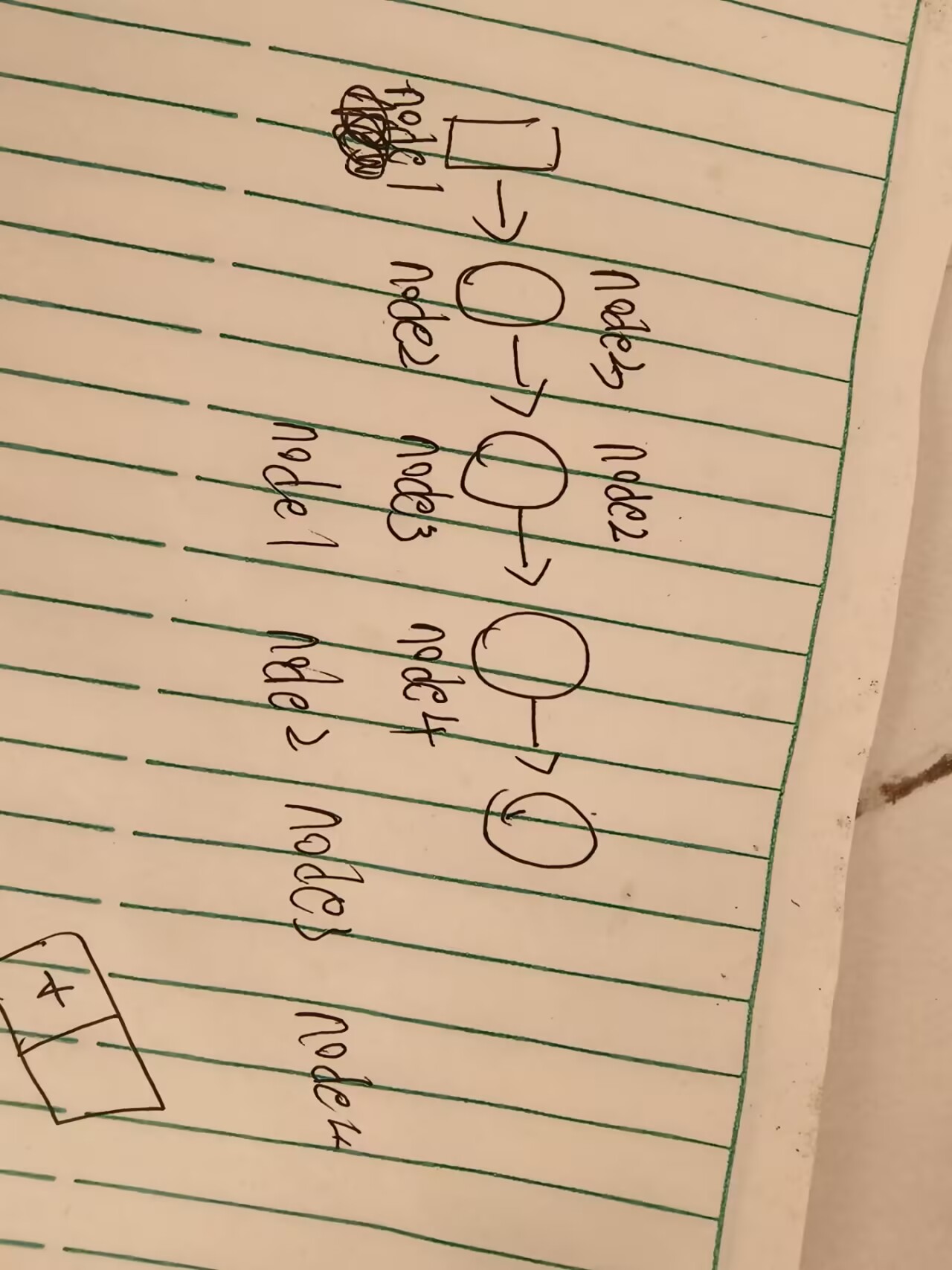
/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {if(head==null || head.next == null)return head;//空链表或者只有一个节点ListNode newHead = new ListNode();//先定义一个虚拟头结点newHead.next = head;//连起来///定义四个变量ListNode node1 , node2 ,node3 ,node4;node1 = newHead;node2 = node1.next;//取next的时候，要防止为nullnode3 = node2.next;//node3==head.nextnode4 = node3.next;while(node1!=null&&node2!=null&node3!=null){//node4为null也可以交换//开始交换node1.next=node3;node3.next = node2;node2.next=node4;//node1~node4往后推进node1 = node2;//node2 = node1.next; if(node2!=null )node3 = node2.next; else node3=null;if(node3!=null) node4 = node3.next; else node4=null;}return newHead.next;}
}

10. 哈希表

10.1 简介

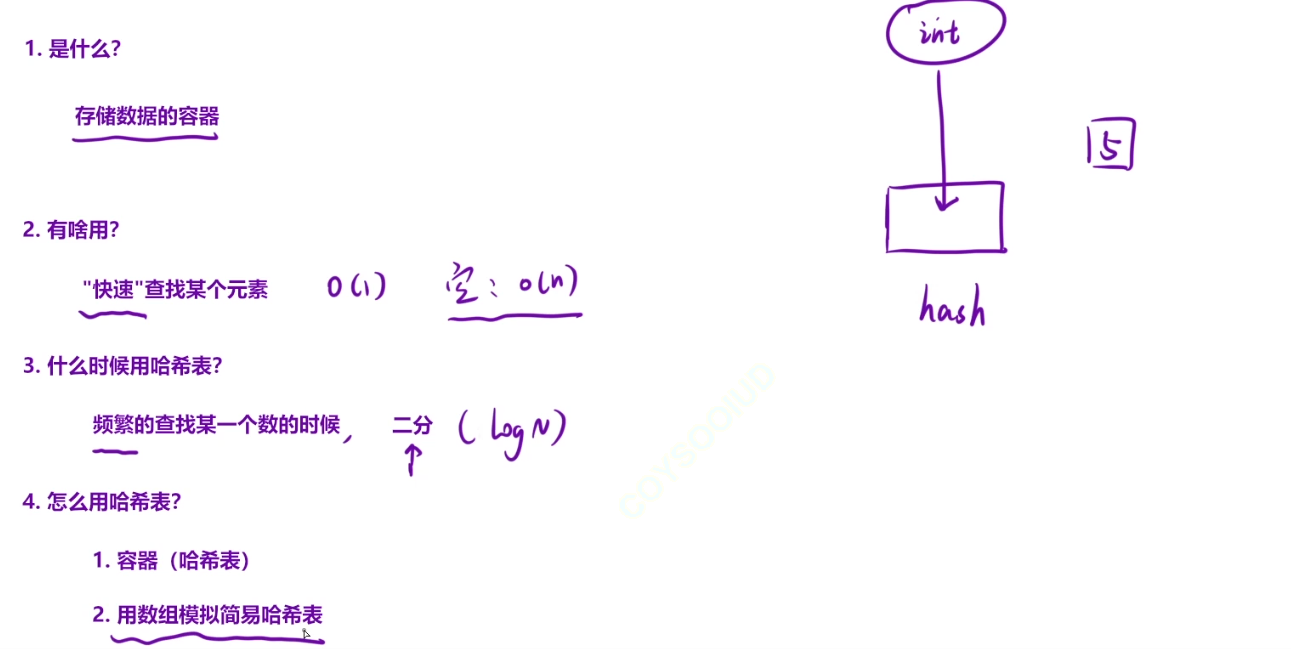
就是查找某个元素，看某个元素在不在哈希表，可以用o(1)的时间复杂度

一般用一个数组来模拟简易的哈希表，一般是数据量比较小，比如1到10^3到107
有负数的时候不要用哈希表

10.2 两数之和

两数之和

暴力解法：

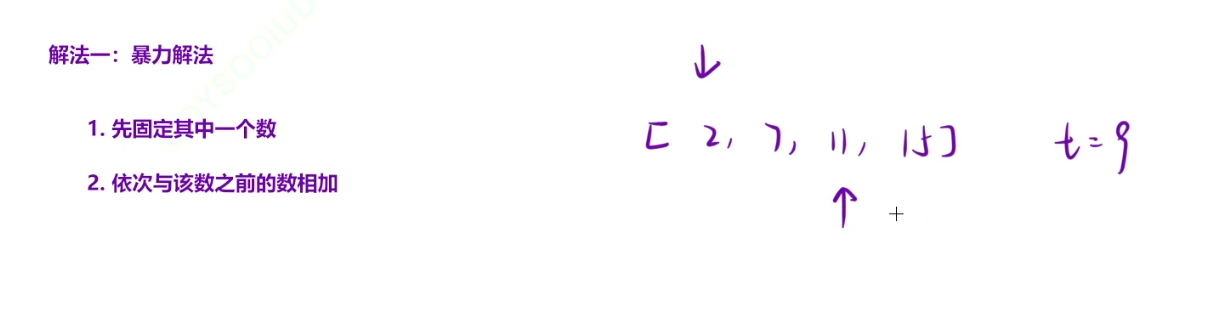
解法二用哈希表，比如遍历到了11，我们可以用9-11=-2，然后找一下数组中是不是存在-2-----》哈希
从左向右遍历，一边遍历，一边把数丢进哈希表中，然后一边判断存不存在9-num[i],是往前面判断的，这个是可行的，是判断前面的数据在不在哈希表
如果不这样，一边丢入，一边判断
那么就可能出现这种情况，如果先全部丢入的话，那么如果target=8，nums[i]=4,那么就可能把这个元素找两次
我们存入的是，nums[i],i

class Solution {public int[] twoSum(int[] nums, int target) {Map<Integer,Integer> map  = new HashMap<>();//nums[i],ifor(int i=0;i<nums.length;i++){int x = target - nums[i];if(map.containsKey(x)){return new int[]{i,map.get(x)};}map.put(nums[i],i);}return new int[]{-1,-1};}
}

注意map的containsKey和get和put方法

10.3 判断是否互为字符重排

判断是否互为字符重排

分析一下
就是判断每个字符的个数是不是一样的–>用hash表
我们可以用数组来模拟
用容器呢—》要比较多次
只有小写–》开26大小
统计第一个串的时候，统计次数
统计第二个的时候，减去个数，看最后是不是全0，或者减为负数的时候，也是错误的
还有就是两个字符串长度不一样的时候，一定false

class Solution {public boolean CheckPermutation(String s1, String s2) {if(s1.length()!=s2.length())return false;int[] arr = new int[26];for(int i=0;i<s1.length();i++){arr[s1.charAt(i)-'a']++;}for(int i=0;i<s2.length();i++){arr[s2.charAt(i)-'a']--;if(arr[s2.charAt(i)-'a']<0)return false;}return  true;}
}

记得，如果字符串长度不相等的话，那么也是错误的

就怕s1的长度太长了，然后出错了

总结