利用千眼狼sCMOS相机开展冷离子云成像与测量实验
1实验背景
冷离子云成像与测量是量子精密测量、多体物理以及量子模拟等前沿交叉领域的重要研究课题,作为理想的孤立量子系统,为验证本征态热化假说(Eigenstate Thermalization Hypothesis, ETH)提供了理想平台。ETH提出多体量子系统的单个本征态可表现出与热平衡态一致的统计行为。
冷离子云成像与测量领域,EMCCD相机成像技术存在以下局限性:
长时间使用面临电子器件老化问题,使用增益不稳定,需频繁校准。
乘性噪声引入,降低了有效量子效率,动态范围受限,难以同步捕获冷离子云的亮/暗区域细节。
工艺复杂,维修困难,体积重量功耗不友好,且进口受限,价格昂贵。
2实验简介
为突破上述局限,某物理实验室,选型一款国产千眼狼高性能sCMOS相机Gloria 1605(图1),此款科学相机拥有800×600分辨率,16μm大像元尺寸,<1 e-低读出噪声,90.7% QE,模数转化位深16Bit,40000:1高动态范围极致参数,可显著提升图像质量与信噪比。实验对象为真空腔内囚禁的冷离子云,配备532 nm激光照亮,sCMOS相机曝光时间设置为100 ms,采用低噪声模式,并通过灵活使用色阶调节对比度增强显示效果的技术,目的提高冷离子云弱信号的可视性。

图1
3实验数据与解析
图2展示了sCMOS相机 Gloria 1605拍摄到的冷离子云图像,从图中可以清晰观察到冷离子云的形态、尺寸以及内部的分布特征。sCMOS相机对极弱信号的捕捉能力强大,保持较高的信噪比,使得离子云的内部结构得以清晰呈现。
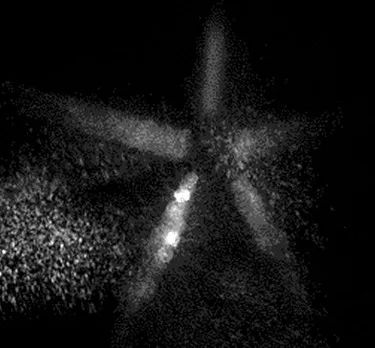
图2
通过时间序列进一步分析,sCMOS相机捕获了冷离子云从非平衡态向稳态弛豫过程(图3),精准量化了局部动力学涨落,同时Gloria 1605的高动态范围特性支持冷离子云亮/暗区域细节的良好呈现。

图3
4实验结论
本次实验表明,利用高性能sCMOS相机可有效进行冷离子云的成像和测量。千眼狼Gloria 1605相机在极弱信号环境下展现出优异的探测性能,清晰捕捉冷离子云在孤立系统中的演化过程,并从中提取关键参数与ETH理论预测进行了对比分析,为该理论在冷离子体系中的适用性提供了有力的实验证据。
