高等数学（工本）----00023 速记宝典

知识点 1 空间直角坐标系的建立

三维空间中几何问题

空间图形形式一点，线，面，体 知识桥梁空间直角坐标系

代数理论表达——坐标，方程(组)

知识点 2 空间直角坐标系的定义

过空间一定点 O ，过该点作三条互相垂直的有向直线 Ox ，Oy ，Oz ，组成一个空间直角坐标系，记为 Oxyz。

l 坐标系的构成特点

l 坐标原点

l 坐标轴(三条) ·坐标面(三个)

l 卦限(八个)

知识点 3  特殊点的坐标

坐标原点 O  （三项为零）

坐标轴上的点（三类）PQR  （两项为零）

坐标面上的点（三类）ABC  （一项为零）

卦限上的点，如：第一卦限的点，各分量全为正

知识点 4   向量的概念

知识点 5 特殊的向量

知识点6 向量的加法

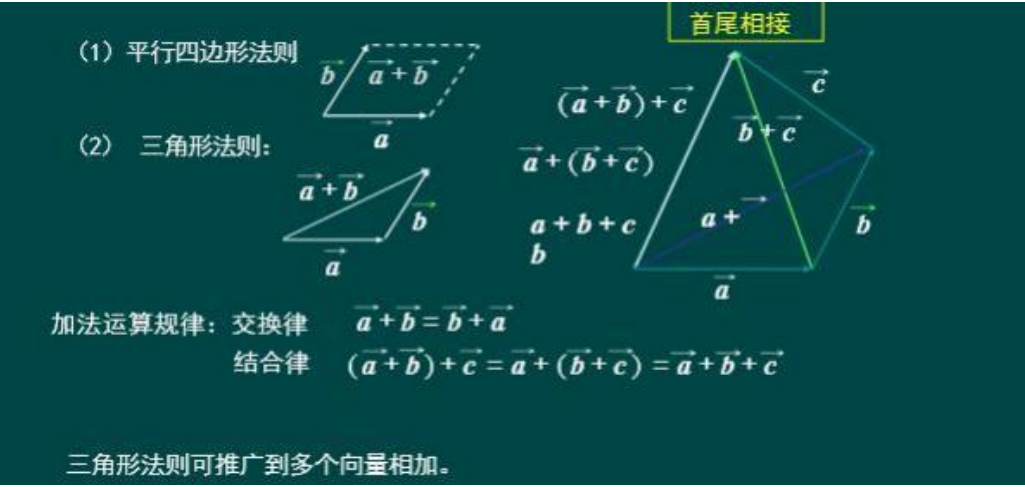
7 向量的减法

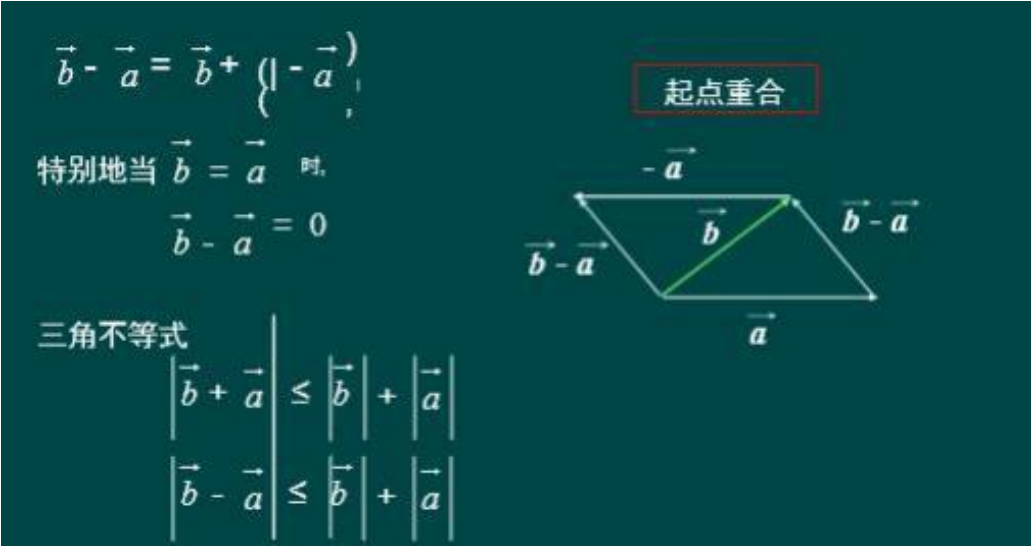
8 向量与数的乘法

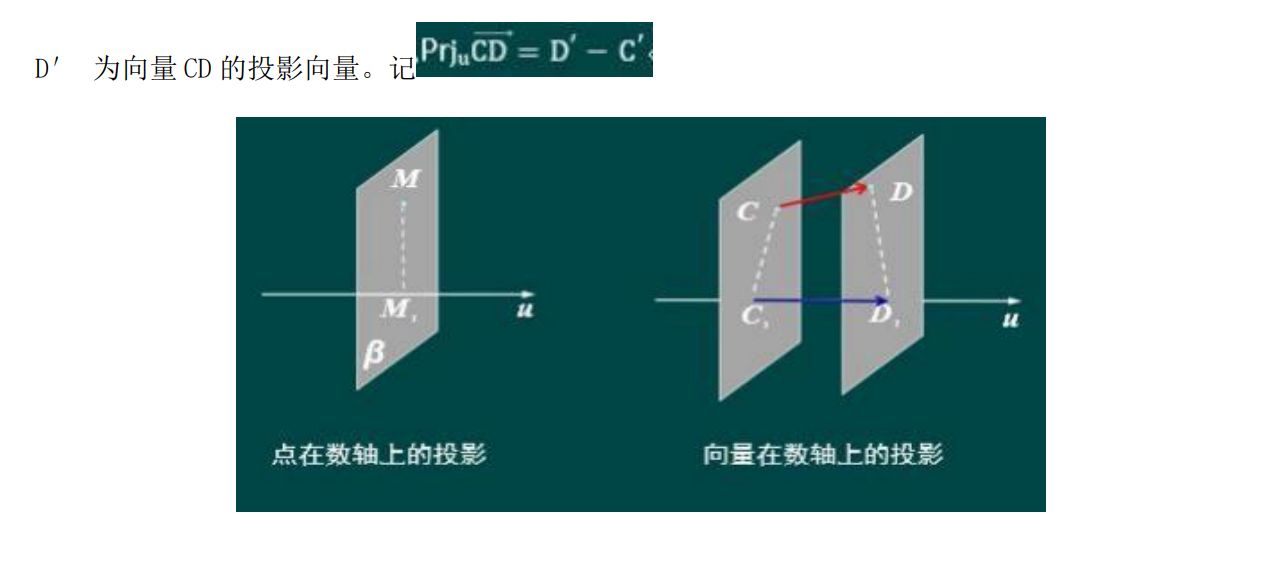
知识点9 向量的投影

（1）点在数轴上的投影  已知空间一点M 与一数轴 u ，过点M 作垂直于数轴 u 的平面阝，且交 点为M ′ ， 则称点 M ′ 为点M在数轴u 上的投影，其中数轴 u 称为投影轴。

（2）向量的投影 设向量 CD 的始点C和终点D在数轴u 上的投影点分别 是C ′为D ′，则称向量 C ′ D ′ 为向量 CD 的投影向量。记

知识点 10 数量积的概念及运算律

定义：给定两个向量 α,阝，它们的数量积为： α.阝 =|α ||阝 |cosφ , φ 是两个向量的夹角。

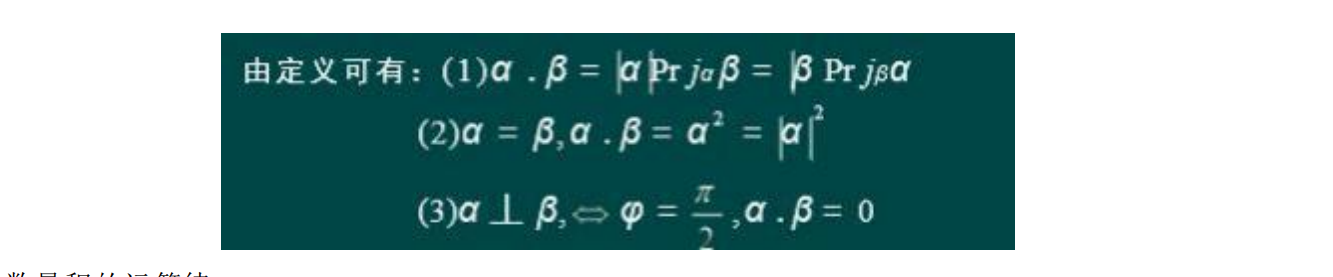
数量积的运算律：

交换律        α .  β =  β .  α

分配律         (  α +   β) .Y =   α .Y +   β .Y

结合律        λ(α .  β) =  λ α +  λβ,  λ ∈ R

知识点 11 数量积的坐标表示

知识点12 曲面方程定义

定义 1 如果曲面 S 与方程F（x，y，z）=0有下述关系：

（1） 曲面 S 上的任意点的坐标都满足此方程

（2）不在曲面 S 上的点的坐标不满足此方程  则F（x，y，z） =0 叫做曲面 S  的方程， 曲面 S  叫 做方程F（x，y，z） = 0 的图形。

知识点 13 曲面关于坐标面的对称性

定理 1 设曲面 S 的方程 F(x ，y ，z )=0，则曲面 S 关于 Oxy 平面 对称的充要条件是，如果点 p (x ，y ，z )的坐标满足方程 F(x ，y , z )= 0，那么必有点 p ′ (x，y，-z )的坐标也满足方程 F(x , y，-z)=0。

简言之， 曲面 S 关于Oxy 平面对称的充要条件是 F(x，y，z) = F(x，y，-z)。

同理可得，曲面 S 关于 Oyz 平面对称的充要条件是 F(-x，y，z) = F(x，y，z)。

曲面 S 关于Ozx 平面对称的充要条件是 F(x，-y，z)=F(x，y，z) 。

知识点 14 直线方程

直线的一般式

定义 直线 L 可视为两平面Π 1， Π2 的交线，设平面Π 1， Π2 的方程为 A1x +B1y +C1z +D1 = 0 , A2x + B2y +C2z + D2  = 0

则方程组

A1x + B1y + C1z + D1  = 0

A2 x + B 2 y + C2 z + D2  = 0

称该方程组为直线 L 的一般式方程。

注：过某定直线的平面有无穷多个，从中任选两个组成的方程组都是交线的一般式方程，一般式方程 不唯一。

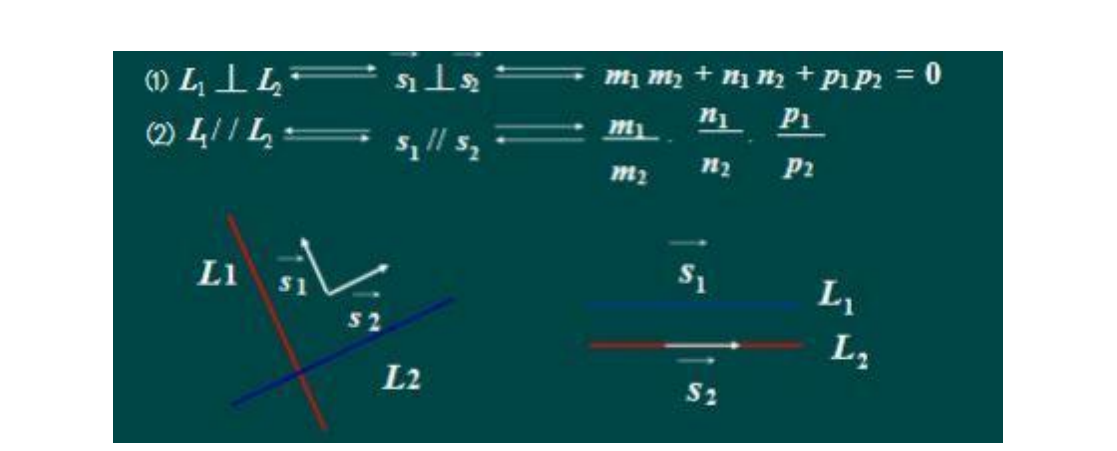
知识点 15 两条直线的夹角

1.两直线的夹角

定义 5 两直线 L1，L2 的方向向量的夹角  θ (取锐角或直角)称为这两条

2. 直线夹角的计算

3.直线的特殊位置关系

知识点 16 二次曲面的概念

1.二次曲面的概念

定义   三元二次方程（二次项系数不全为 0）

Ax2 + By2 + Cz2 + Dxy + Eyz + Fzx + Gx + Hy + Iz + J = 0 所表示的空间曲面称为二次曲面。 2. 常见二次曲面

椭球面、抛物面、双曲面

研究二次曲面特性的基本方法：截痕法

知识点 17 二元函数的定义

定义 1 设有三个变量 x，y，z ，当变量 x，y 在一定范围 D 内任取一 对数值时，按照一定的对应

法则，总有 唯一确定的数值 z 与之对应， 则称变量 z 为变量 x，y 的二元函数，记作 z = f（ x ，y）

自变量 x，y 的变化范围 D 称为该二元函数的定义域。

因变量 z 的变化范围称为该二元函数的值域，记作    R = { z/z = f (x ，y ) , (x ，y ) ∈ D  }

知识点18 定义域的求解

定义域求法：（1）分式的分母不能为零；

（2）偶次根函数被开方值非负；

（3）对数函数的真数为正数；

（4）函数相加时，定义域为两项定义域的交集。

知识点19 二元函数的有界性

定义 3 设函数 f  (x，y) 在点集 D 上有定义，如果存在 M>0 ，使  得 对于任何（x，y） ∈D ，都

有|f（x，y） | ≤M  成立，则称 f ( x ，y ) 在 D 上的有界函数，否则称为无界函数。

知识点20 二元函数的间断点

若函数 z=(x,y)在点 PoXo,yo)满足上述三个条件 中的一条，则称函数在点   处不连续或间断，且称

点是函数的间断点

知识点 21 最值定理

二元连续函数在其定义区域上必然可取到最大值 M 和最小值m，且 函数在定义域上必有界（有界定 理）。