周志华院士西瓜书实战（二）MLP+SVM+贝叶斯分类器+决策树+集成学习

1. MLP 多层感知机

1.把[0,255]灰度图 归一化为[0,1]   2.划分训练/测试集   3.创建模型设置参数   4.fit训练   5.再评估

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report# 加载数据
mnist = fetch_openml('mnist_784', as_frame=False)
X, y = mnist.data, mnist.target
X = X / 255.0  # 归一化到[0,1]# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建MLP模型
mlp = MLPClassifier(hidden_layer_sizes=(50, 50),  # 2个隐藏层，每层50个神经元activation='relu',           # 激活函数solver='adam',               # 优化器alpha=1e-4,                 # L2正则化系数batch_size=256,             # 批量大小learning_rate_init=0.001,   # 初始学习率max_iter=20,                # 最大迭代次数random_state=42
)# 训练模型
mlp.fit(X_train, y_train)# 评估模型
y_pred = mlp.predict(X_test)
print(classification_report(y_test, y_pred))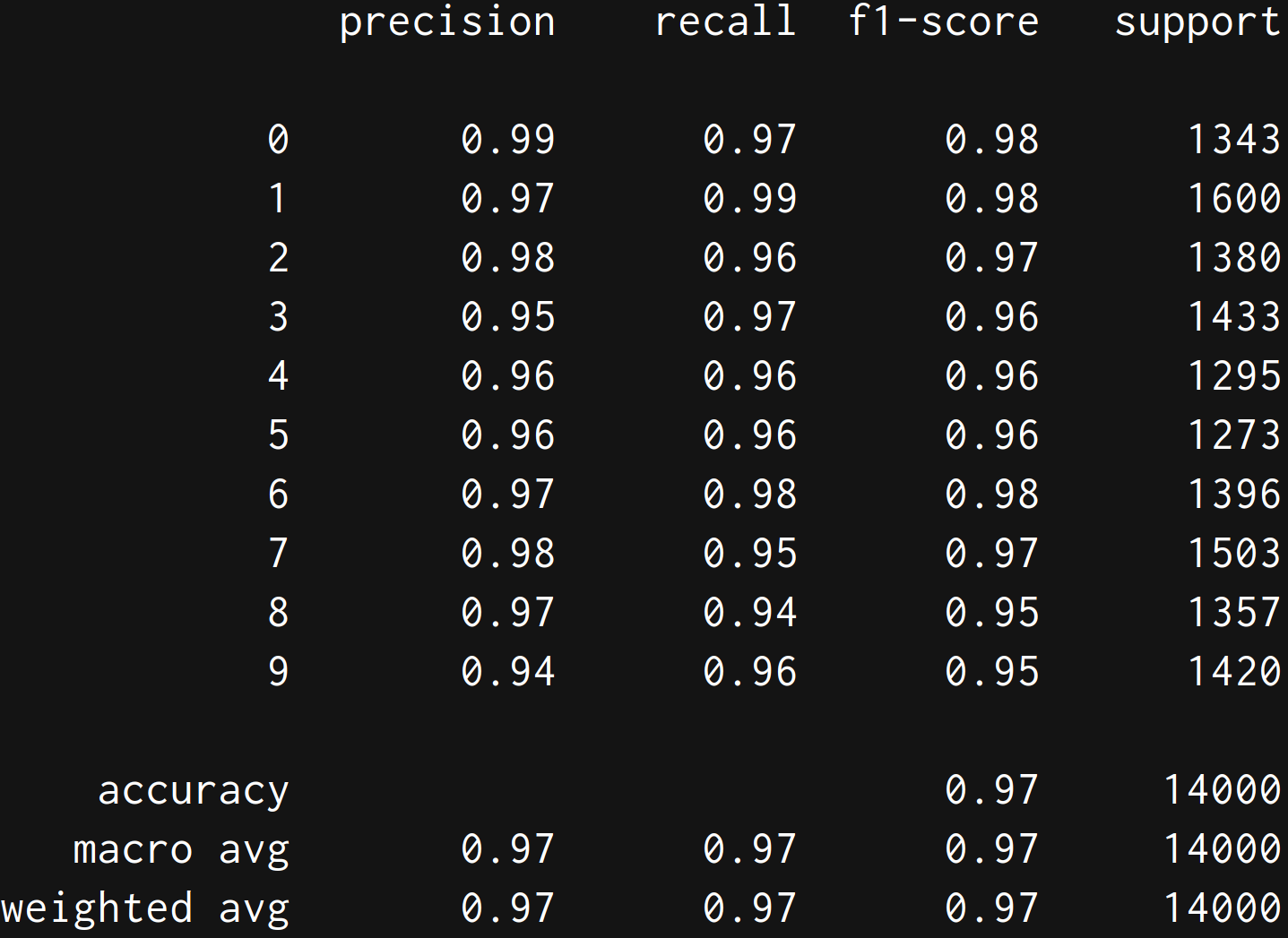

2. SVM支持向量机

周志华《机器学习导论》第5章 支持向量机SVM_支持向量机导论 李国正 目录-CSDN博客

2.1 线性SVM    要设置kernel和正则化参数

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svmdata = np.array([[0.1, 0.7],[0.3, 0.6],[0.4, 0.1],[0.5, 0.4],[0.8, 0.04],[0.42, 0.6],[0.9, 0.4],[0.6, 0.5],[0.7, 0.2],[0.7, 0.67],[0.27, 0.8],[0.5, 0.72]
])# 建立数据集
label = [1] * 6 + [0] * 6 #前六个数据的label为1后六个为0
model_linear = svm.SVC(kernel='linear', C = 0.001)# 线性svm
model_linear.fit(data, label) # 训练

建立meshgrid网格 将预测结果可视化

x_min, x_max = data[:, 0].min() - 0.2, data[:, 0].max() + 0.2
y_min, y_max = data[:, 1].min() - 0.2, data[:, 1].max() + 0.2
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.002),np.arange(y_min, y_max, 0.002)) # meshgrid如何生成网格Z = model_linear.predict(np.c_[xx.ravel(), yy.ravel()]) # 预测
# 将xx yy 展平后  两两对应组合为 每个点两个坐标
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap = plt.cm.ocean, alpha=0.6) #不同区域填充颜色
plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
plt.title('Linear SVM')
plt.show()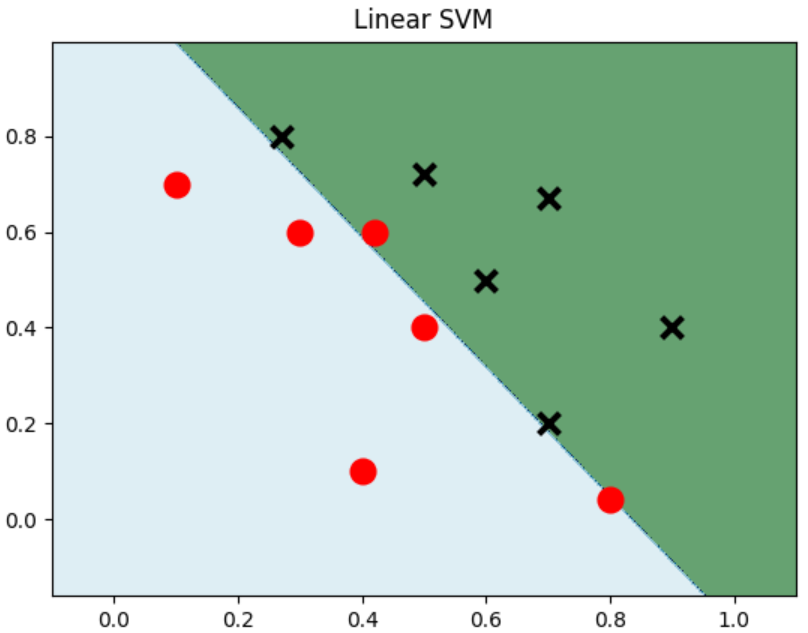

2.2 多项式核  设置多项式核，正则化参数，次数

model_poly = svm.SVC(C=0.0001, kernel='poly', degree=degree)

# 多项式核
plt.figure(figsize=(16, 15))for i, degree in enumerate([1, 3, 5, 7, 9, 12]):  # 多项式次数选择了1,3,5,7,9,12# C: 惩罚系数，gamma: 高斯核的系数model_poly = svm.SVC(C=0.0001, kernel='poly', degree=degree)  # 多项式核model_poly.fit(data, label)  # 训练Z = model_poly.predict(np.c_[xx.ravel(), yy.ravel()])  # 预测Z = Z.reshape(xx.shape)plt.subplot(3, 2, i + 1)plt.subplots_adjust(wspace=0.4, hspace=0.4)plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)# 画出训练点plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)plt.title('Poly SVM with $\degree=$' + str(degree))
plt.show()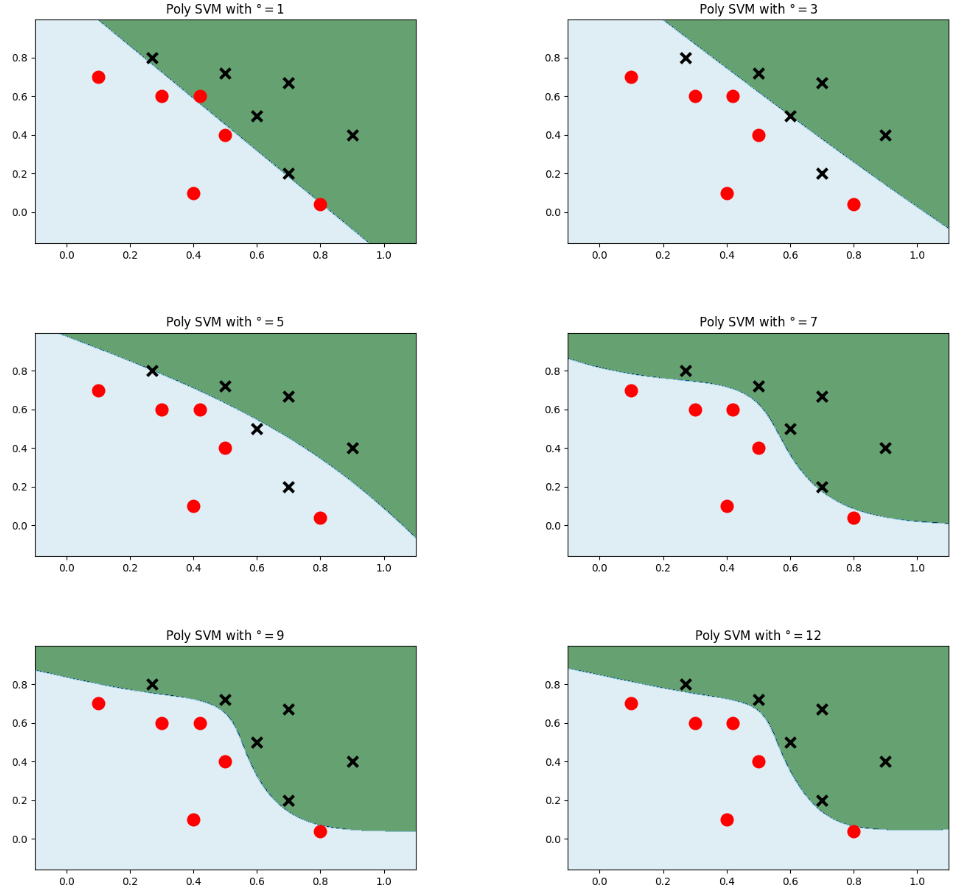

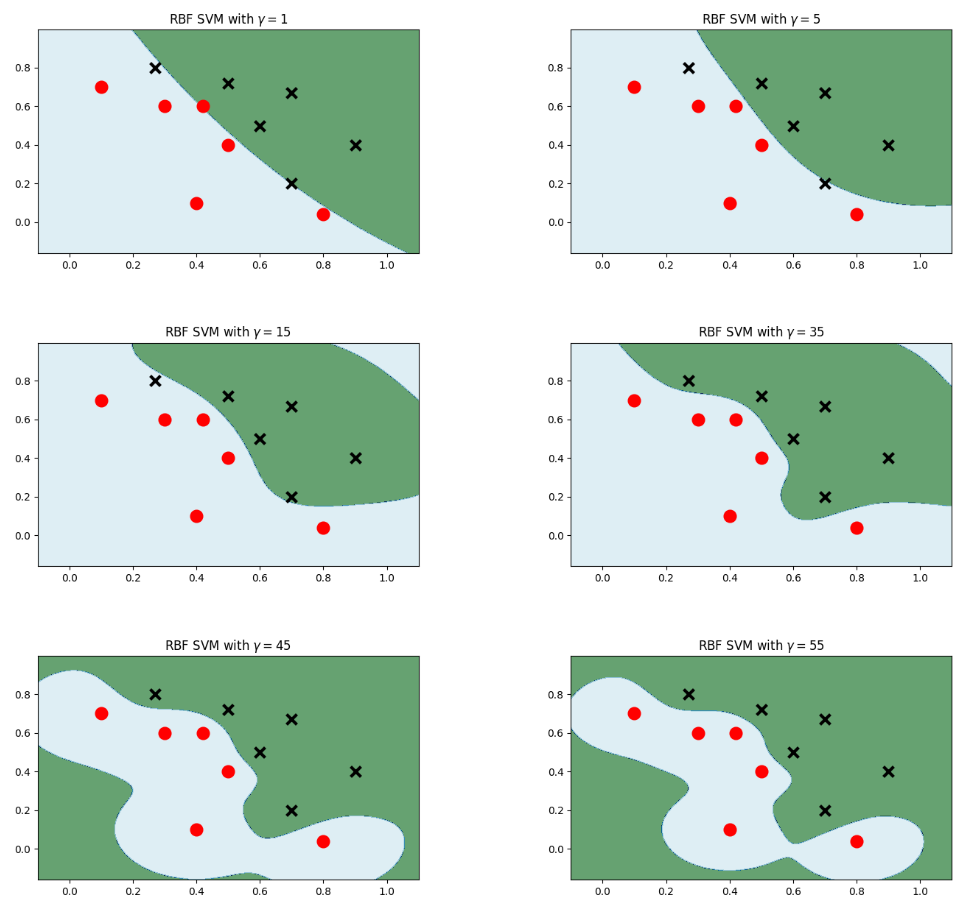
3. 高斯核复杂非线性    三种复杂性由简单到复杂为：
model_linear = svm.SVC(kernel='linear', C = 0.001) 线性
model_poly = svm.SVC(C=0.0001, kernel='poly', degree=degree) 多项式
model_rbf = svm.SVC(kernel='rbf', gamma=gamma, C=0.0001) 高斯核

3. SVM MNIST

clf = GridSearchCV(SVC(), {'kernel':['rbf','linear'], 'C':[0.1,1,10], 'gamma':[0.01, 0.1]}, n_jobs=-1)

建立SVC Support Vector Classifier 并进行gridsearch

from sklearn.datasets import fetch_openml
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV
from time import time
X, y = fetch_openml('mnist_784', version=1, as_frame=False, return_X_y=True)# 直接划分训练测试集 + 限制样本量
X_train, y_train = X[:2000], y[:2000].astype(int)
X_test, y_test = X[60000:60200], y[60000:60200].astype(int)print("Training...")
start = time()
clf = GridSearchCV(SVC(), {'kernel':['rbf','linear'], 'C':[0.1,1,10], 'gamma':[0.01, 0.1]}, n_jobs=-1)
clf.fit(X_train, y_train)
train_time = time() - start
print(f'Train: {train_time // 60:.0f}min {train_time % 60:.3f}sec')# 输出最佳结果
print("最佳参数：", clf.best_params_)
print("最佳模型得分：", clf.best_score_)
print(f"Test Accuracy: {clf.score(X_test, y_test):.3f}")

4. 贝叶斯分类器

周志华《机器学习导论》第7章 贝叶斯分类器-CSDN博客

from sklearn.naive_bayes import GaussianNB
model = GaussianNB() #朴素贝叶斯

用make_blobs 产生聚类数据；再进行训练 可视化

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
#生成随机数据
# make_blobs：为聚类产生数据集
# n_samples：样本点数，n_features：数据的维度，centers:产生数据的中心点，默认值3
# cluster_std：数据集的标准差，浮点数或者浮点数序列，默认值1.0，random_state：随机种子
X, y = make_blobs(n_samples = 100, n_features=2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
plt.show()from sklearn.naive_bayes import GaussianNB
model = GaussianNB()#朴素贝叶斯
model.fit(X, y)# 训练模型
rng = np.random.RandomState(0)
X_test = [-6, -14] + [14, 18] * rng.rand(2000, 2)#生成训练集
y_pred = model.predict(X_test)
# 将训练集和测试集的数据用图像表示出来，颜色深直径大的为训练集，颜色浅直径小的为测试集
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
lim = plt.axis()
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_pred, s=20, cmap='RdBu', alpha=0.1)
plt.axis(lim)
plt.show()yprob = model.predict_proba(X_test)#返回的预测值为，每条数据对每个分类的概率
print(yprob[-8:].round(2))

5. 决策树

周志华《机器学习导论》第4章 决策树-CSDN博客

葡萄酒问题：数据准备 预处理 划分训练集（后面几个 都是如此初始化）

import pandas as pd
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import accuracy_score, classification_report
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt# 加载数据
wine = load_wine()
print(f"所有特征：{wine.feature_names}")# 创建DataFrame
X = pd.DataFrame(wine.data, columns=wine.feature_names)
y = pd.Series(wine.target)# 数据预处理 - 标准化
X_scaled = StandardScaler().fit_transform(X)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.20, random_state=1, stratify=y)

grid_search 找最佳模型

# 设置参数网格
param_grid = {'max_depth': [2, 3, 4, 5, 6, None],'min_samples_split': [2, 5, 10],'min_samples_leaf': [1, 2, 4],'criterion': ['gini', 'entropy'],'max_features': ['sqrt', 'log2']
}# 网格搜索
grid_search = GridSearchCV(DecisionTreeClassifier(random_state=1),param_grid=param_grid,cv=5,n_jobs=-1,verbose=1)# 训练模型
grid_search.fit(X_train, y_train)
# 最佳模型
best_dt = grid_search.best_estimator_
# 预测
y_pred = best_dt.predict(X_test)

结果评估 + 决策树可视化 + 特征重要性

# 评估
print(f"最佳参数：{grid_search.best_params_}")
print(f"优化后的决策树准确率：{accuracy_score(y_test, y_pred):.4f}")
print("\n分类报告：")
print(classification_report(y_test, y_pred))# 可视化决策树
plt.figure(figsize=(20,10))
plot_tree(best_dt,feature_names=wine.feature_names,class_names=wine.target_names,filled=True,rounded=True)
plt.show()# 特征重要性
feature_imp = pd.Series(best_dt.feature_importances_,index=wine.feature_names).sort_values(ascending=False)
print("\n特征重要性：")
print(feature_imp)

6. 集成学习系列 grid_search参数

周志华《机器学习导论》第8章 集成学习 Ensemble Learning-CSDN博客

Bagging  投票器数目n + 采样比例

随机森林   决策树数目 + 决策树参数

AdaBoost   投票器数目n + 学习率

6.1 Bagging 重叠采样

决策树投票     需要决策树的estimator=base_model     需要grid_search  投票器数目n和采样比例

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier# 基础模型和参数网格
base_model = DecisionTreeClassifier(max_depth=3, min_samples_split=5, random_state=42)
param_grid = {'n_estimators': range(10, 100, 10),  # 10-90，步长10'max_samples': [0.8, 0.9] # 采样比例
}# 使用GridSearchCV
grid_search = GridSearchCV(BaggingClassifier(estimator=base_model, random_state=42),param_grid, cv=5, n_jobs=-1,  scoring='accuracy'
)
grid_search.fit(X_train, y_train)# 输出最佳结果
print(f"最佳参数: {grid_search.best_params_}")
print(f"交叉验证最佳准确率: {grid_search.best_score_:.3f}")
print(f"测试集准确率: {grid_search.score(X_test, y_test):.3f}")

6.2 随机森林

初始化部分与上面相同               参数比决策树多一个n_estimators

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
param_grid = {'n_estimators': [50, 100, 200],'max_depth': [None, 5, 10],'min_samples_split': [2, 5],'max_features': ['sqrt', 'log2']
}grid_search = GridSearchCV(RandomForestClassifier(random_state=42),param_grid,cv=5,n_jobs=-1)
grid_search.fit(X_train, y_train)print("最佳参数:", grid_search.best_params_)

6.3 AdaBoost

from sklearn.ensemble import AdaBoostClassifier
from sklearn.model_selection import GridSearchCV, train_test_split
hyperparameter_space = {'n_estimators': list(range(2, 42, 2)),  # 2-40，步长2'learning_rate': [0.1, 0.2, 0.3, 0.5, 0.8, 1.0]  # 学习率
}# GridSearchCV优化
gs = GridSearchCV(AdaBoostClassifier(random_state=1),param_grid=hyperparameter_space,scoring="accuracy",n_jobs=-1,cv=5,verbose=1
)gs.fit(X_train, y_train)
# 输出结果
print("最优超参数:", gs.best_params_)
print("交叉验证最佳准确率: {:.3f}".format(gs.best_score_))
print("测试集准确率: {:.3f}".format(accuracy_score(y_test, gs.predict(X_test))))