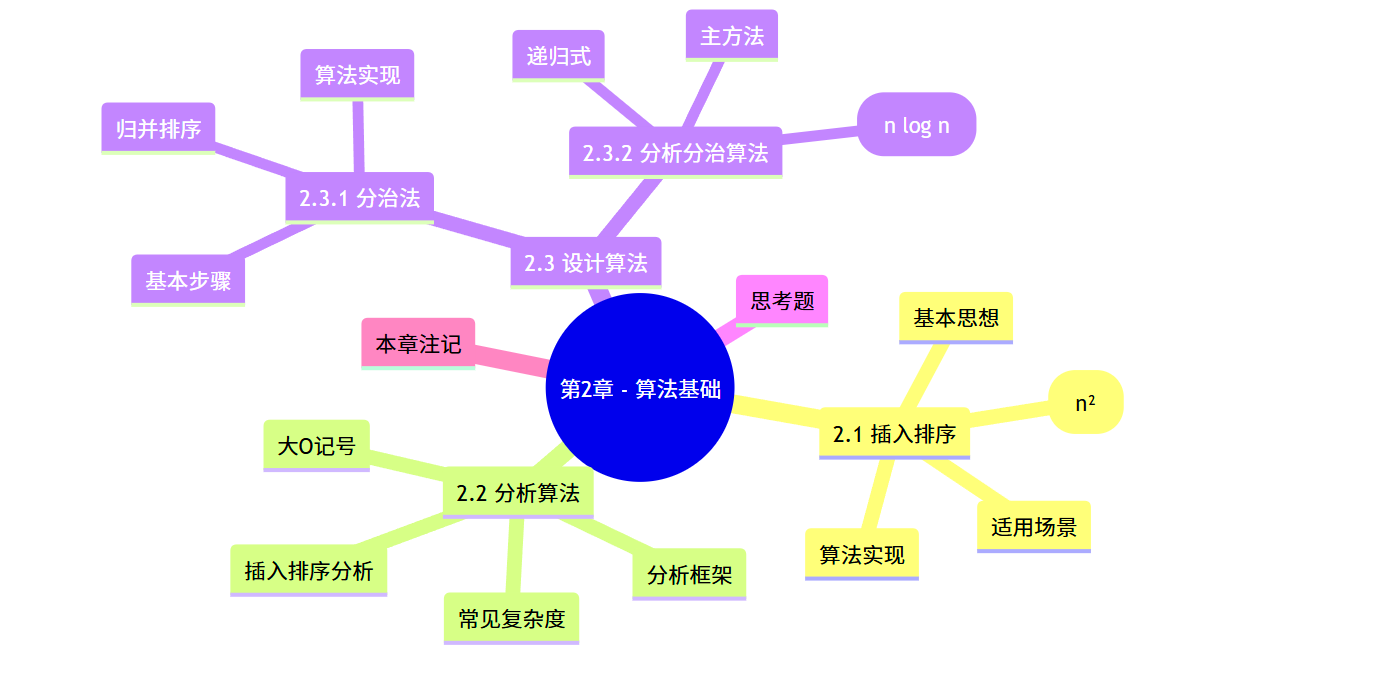
《算法导论》第 2 章 - 算法基础
大家好,今天我们来一起学习《算法导论》的第 2 章 —— 算法基础。这一章是算法学习的入门内容,主要介绍了两种经典排序算法(插入排序和归并排序)以及算法分析的基本方法,非常适合初学者打好基础。本文会结合实例代码和图解,帮助大家更好地理解和掌握这些知识点。

2.1 插入排序
插入排序是一种简单直观的排序算法,它的工作原理类似于我们整理手中的扑克牌。
基本思想
插入排序的基本思想是:将待排序的元素逐个插入到已经排好序的部分数组中,直到所有元素都插入完毕。
具体步骤如下:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤 3,直到找到已排序的元素小于或等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤 2~5
插入排序代码实现(C++)
下面是插入排序的完整 C++ 代码,包含详细注释:
#include <iostream>
#include <vector>using namespace std;/*** 插入排序函数* @param arr 待排序的数组(引用传递,直接修改原数组)*/
void insertionSort(vector<int>& arr) {int n = arr.size(); // 获取数组长度// 从第二个元素开始遍历(第一个元素默认已排序)for (int i = 1; i < n; i++) {int key = arr[i]; // 取出当前要插入的元素int j = i - 1; // 已排序部分的最后一个元素索引// 将大于key的元素向后移动一位while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key; // 将key插入到正确位置}
}/*** 打印数组元素* @param arr 要打印的数组*/
void printArray(const vector<int>& arr) {for (int num : arr) {cout << num << " ";}cout << endl;
}int main() {// 测试案例vector<int> arr = {5, 2, 4, 6, 1, 3};cout << "排序前的数组: ";printArray(arr);insertionSort(arr); // 调用插入排序cout << "排序后的数组: ";printArray(arr);return 0;
}
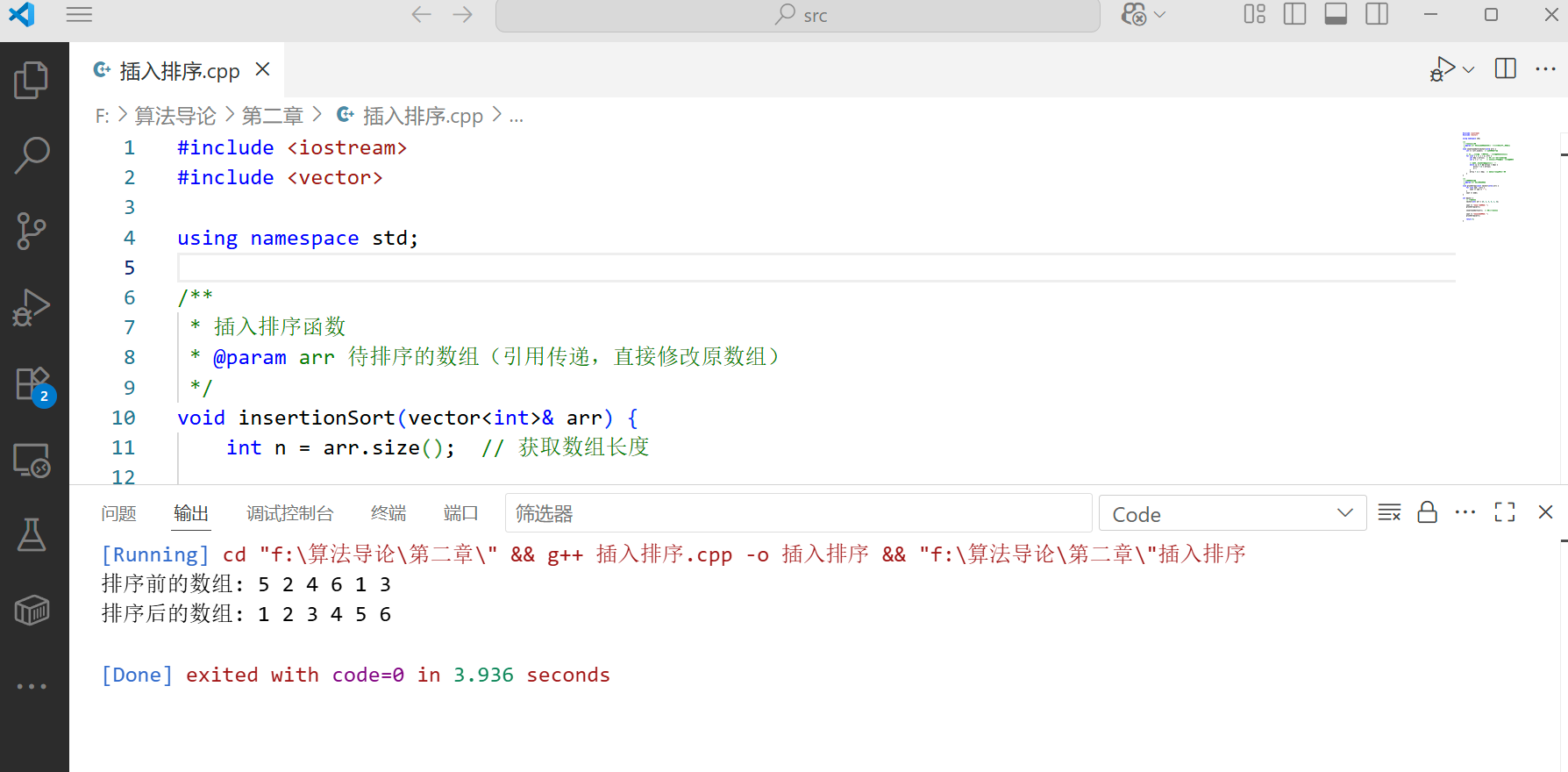
这段代码可以直接编译运行,它实现了对整数数组的插入排序。我们使用了 vector 容器来存储数组元素,使得代码更加灵活。
插入排序综合案例:学生成绩排序
下面我们来看一个更实际的应用案例:对学生成绩进行排序。我们将创建一个 Student 类,包含学生姓名和成绩,然后使用插入排序按照成绩从高到低进行排序。
#include <iostream>
#include <vector>
#include <string>using namespace std;/*** 学生类*/
class Student {
private:string name; // 姓名int score; // 成绩public:// 构造函数Student(string n, int s) : name(n), score(s) {}// 获取姓名string getName() const { return name; }// 获取成绩int getScore() const { return score; }// 重载大于运算符,用于比较成绩bool operator>(const Student& other) const {return score > other.score;}
};/*** 插入排序函数(对学生数组按成绩从高到低排序)* @param students 待排序的学生数组*/
void insertionSort(vector<Student>& students) {int n = students.size();for (int i = 1; i < n; i++) {Student key = students[i]; // 当前要插入的学生int j = i - 1;// 将成绩低于key的学生向后移动while (j >= 0 && students[j] > key) {students[j + 1] = students[j];j--;}students[j + 1] = key; // 插入到正确位置}
}/*** 打印学生信息* @param students 学生数组*/
void printStudents(const vector<Student>& students) {cout << "姓名\t成绩" << endl;cout << "----------------" << endl;for (const auto& s : students) {cout << s.getName() << "\t" << s.getScore() << endl;}
}int main() {// 创建学生数组vector<Student> students = {Student("张三", 85),Student("李四", 92),Student("王五", 78),Student("赵六", 90),Student("钱七", 88)};cout << "排序前的学生成绩:" << endl;printStudents(students);insertionSort(students); // 按成绩排序cout << "\n排序后的学生成绩(从低到高):" << endl;printStudents(students);return 0;
}
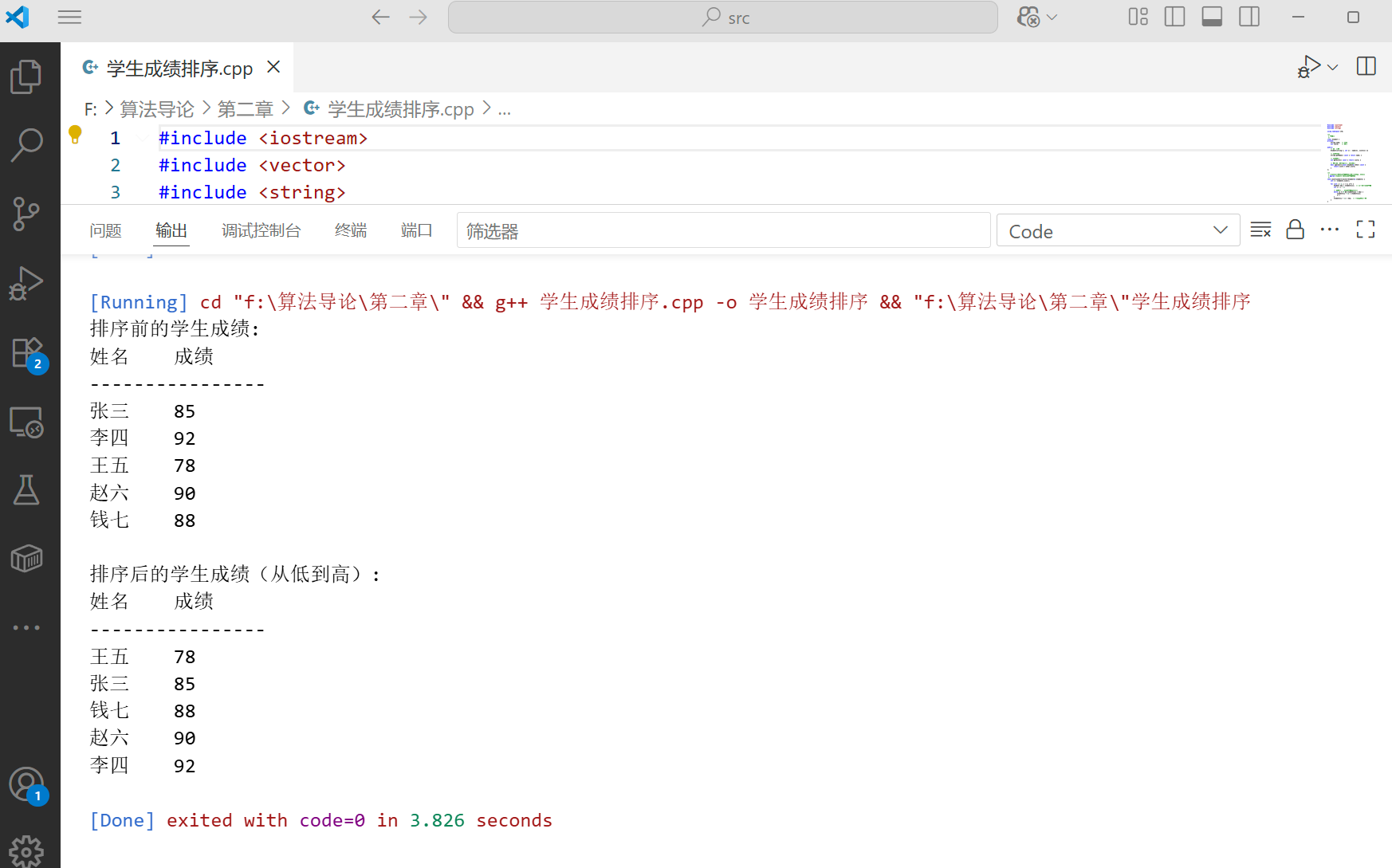
这个案例展示了插入排序在实际应用中的用法。我们通过重载>运算符,使得插入排序算法可以直接用于 Student 对象的比较,体现了面向对象编程的灵活性。

2.2 分析算法
分析算法的目的是预测算法的资源消耗,以便比较不同算法的性能。在大多数情况下,我们最关心的是算法的运行时间。
分析框架
我们通常从以下几个方面分析算法:
- 最坏情况分析:确定算法在输入规模为 n 时的最大运行时间
- 最好情况分析:确定算法在输入规模为 n 时的最小运行时间
- 平均情况分析:确定算法在所有可能输入上的平均运行时间
在实际应用中,我们通常更关注最坏情况分析,因为:
- 它给出了算法运行时间的上界,保证了算法不会比这更差
- 对于某些算法,最坏情况经常出现
- 平均情况分析往往比较复杂
大 O 记号
在算法分析中,我们使用大 O 记号来描述算法的时间复杂度。大 O 记号表示的是算法运行时间的增长率上限。
例如,插入排序的最坏情况时间复杂度是 O (n²),表示当输入规模 n 足够大时,插入排序的运行时间不会超过 n² 的某个常数倍。
常见的时间复杂度按增长率从小到大排列:
- O (1):常数时间
- O (log n):对数时间
- O (n):线性时间
- O (n log n):线性对数时间
- O (n²):平方时间
- O (n³):立方时间
- O (2ⁿ):指数时间
插入排序的时间复杂度分析
我们来分析一下插入排序的时间复杂度:
最好情况:当输入数组已经排好序时,内层循环不需要执行元素移动操作。
- 时间复杂度:O (n)
最坏情况:当输入数组逆序排列时,每个元素都需要与前面所有已排序的元素进行比较和移动。
- 时间复杂度:O (n²)
平均情况:考虑所有可能的输入排列,平均情况下的时间复杂度也是 O (n²)
| 情况 | 时间复杂度 | 说明 |
|---|---|---|
| 最好情况 | O(n) | 数组已经有序 |
| 最坏情况 | O(n²) | 数组完全逆序 |
| 平均情况 | O(n²) | 随机排列的数组 |
算法分析案例:比较不同规模数据的排序时间
下面的代码演示了插入排序在不同规模数据上的运行时间,帮助我们直观感受算法复杂度的含义:
#include <iostream>
#include <vector>
#include <chrono> // 用于计时
#include <cstdlib> // 用于生成随机数
#include <algorithm> // 用于reverseusing namespace std;
using namespace chrono;// 插入排序函数
void insertionSort(vector<int>& arr) {int n = arr.size();for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}
}// 生成随机数组
vector<int> generateRandomArray(int size) {vector<int> arr(size);for (int i = 0; i < size; i++) {arr[i] = rand() % 10000; // 生成0-9999的随机数}return arr;
}// 测试插入排序在不同规模数据上的运行时间
void testInsertionSortPerformance() {// 测试不同规模的数组vector<int> sizes = {1000, 2000, 4000, 8000, 16000};cout << "测试插入排序性能:" << endl;cout << "数组规模\t最好情况(ms)\t最坏情况(ms)\t随机情况(ms)" << endl;cout << "---------------------------------------------------------" << endl;for (int size : sizes) {// 生成三种情况的数组vector<int> bestCase(size);for (int i = 0; i < size; i++) bestCase[i] = i; // 已排序(最好情况)vector<int> worstCase = bestCase;reverse(worstCase.begin(), worstCase.end()); // 逆序(最坏情况)vector<int> randomCase = generateRandomArray(size); // 随机数组(平均情况)// 测试最好情况auto start = high_resolution_clock::now();insertionSort(bestCase);auto end = high_resolution_clock::now();auto bestTime = duration_cast<milliseconds>(end - start).count();// 测试最坏情况start = high_resolution_clock::now();insertionSort(worstCase);end = high_resolution_clock::now();auto worstTime = duration_cast<milliseconds>(end - start).count();// 测试随机情况start = high_resolution_clock::now();insertionSort(randomCase);end = high_resolution_clock::now();auto randomTime = duration_cast<milliseconds>(end - start).count();// 输出结果cout << size << "\t\t" << bestTime << "\t\t" << worstTime << "\t\t" << randomTime << endl;}
}int main() {testInsertionSortPerformance();return 0;
}
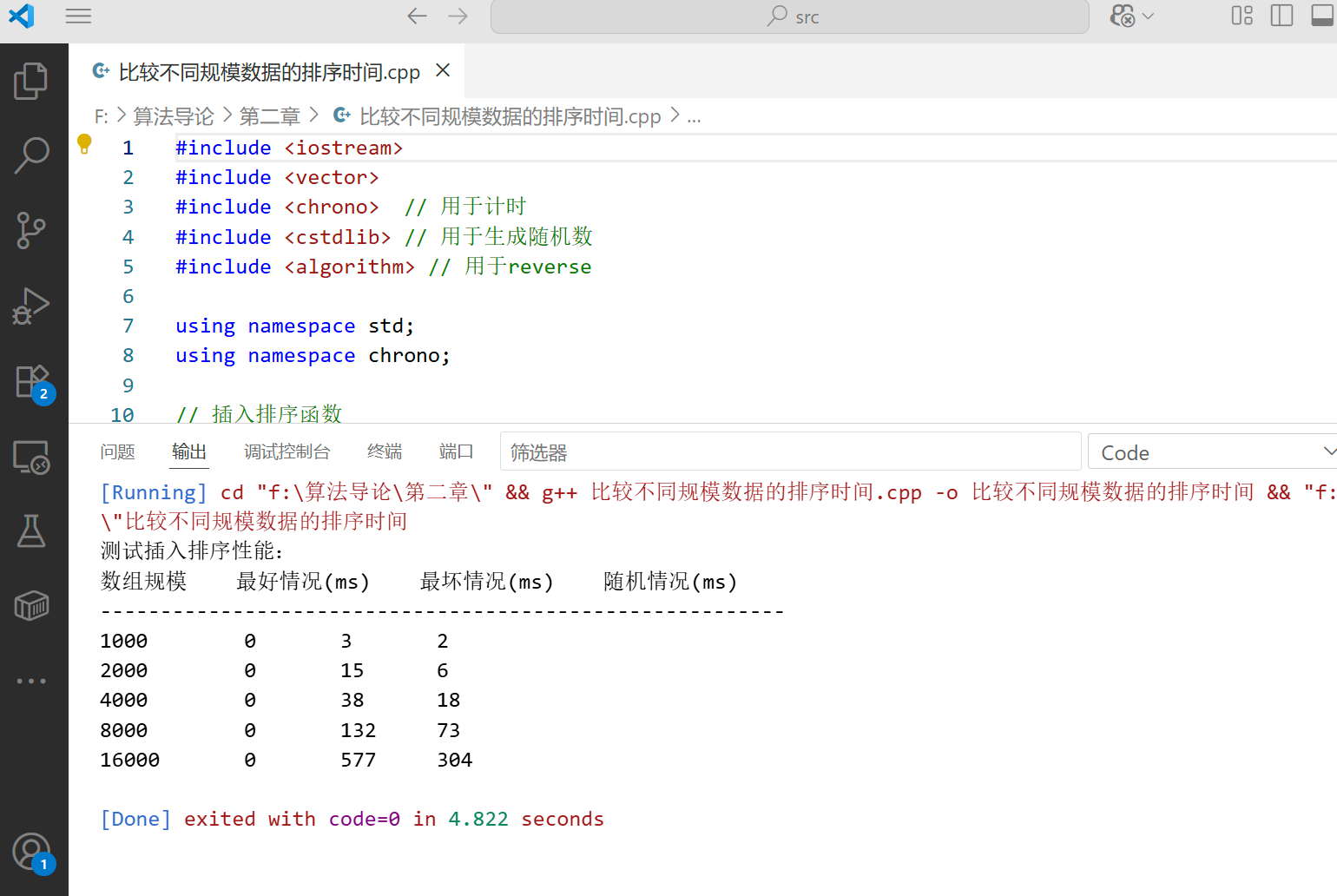
运行这段代码,你会发现当数组规模翻倍时,最坏情况和随机情况下的运行时间大约会增加到原来的 4 倍(符合 O (n²) 的特征),而最好情况下的运行时间大约会增加到原来的 2 倍(符合 O (n) 的特征)。
2.3 设计算法
算法设计是指从问题出发,构造出求解问题的有效算法的过程。常用的算法设计方法有:分治法、动态规划、贪心算法、回溯法等。本章重点介绍分治法。
2.3.1 分治法
分治法(Divide and Conquer)是一种非常重要的算法设计思想,其基本思想是:
- 分解(Divide):将原问题分解为若干个规模较小、结构与原问题相似的子问题
- 解决(Conquer):递归地解决这些子问题。如果子问题的规模足够小,则直接求解
- 合并(Combine):将子问题的解合并为原问题的解
分治法的典型应用是归并排序(Merge Sort)。
归并排序的基本思想
归并排序正是基于分治法的思想实现的:
- 分解:将 n 个元素分成两个各含 n/2 个元素的子序列
- 解决:递归地对两个子序列进行归并排序
- 合并:合并两个已排序的子序列,得到最终的排序结果
归并排序的关键在于合并步骤:如何高效地合并两个已排序的子序列。
归并排序流程图
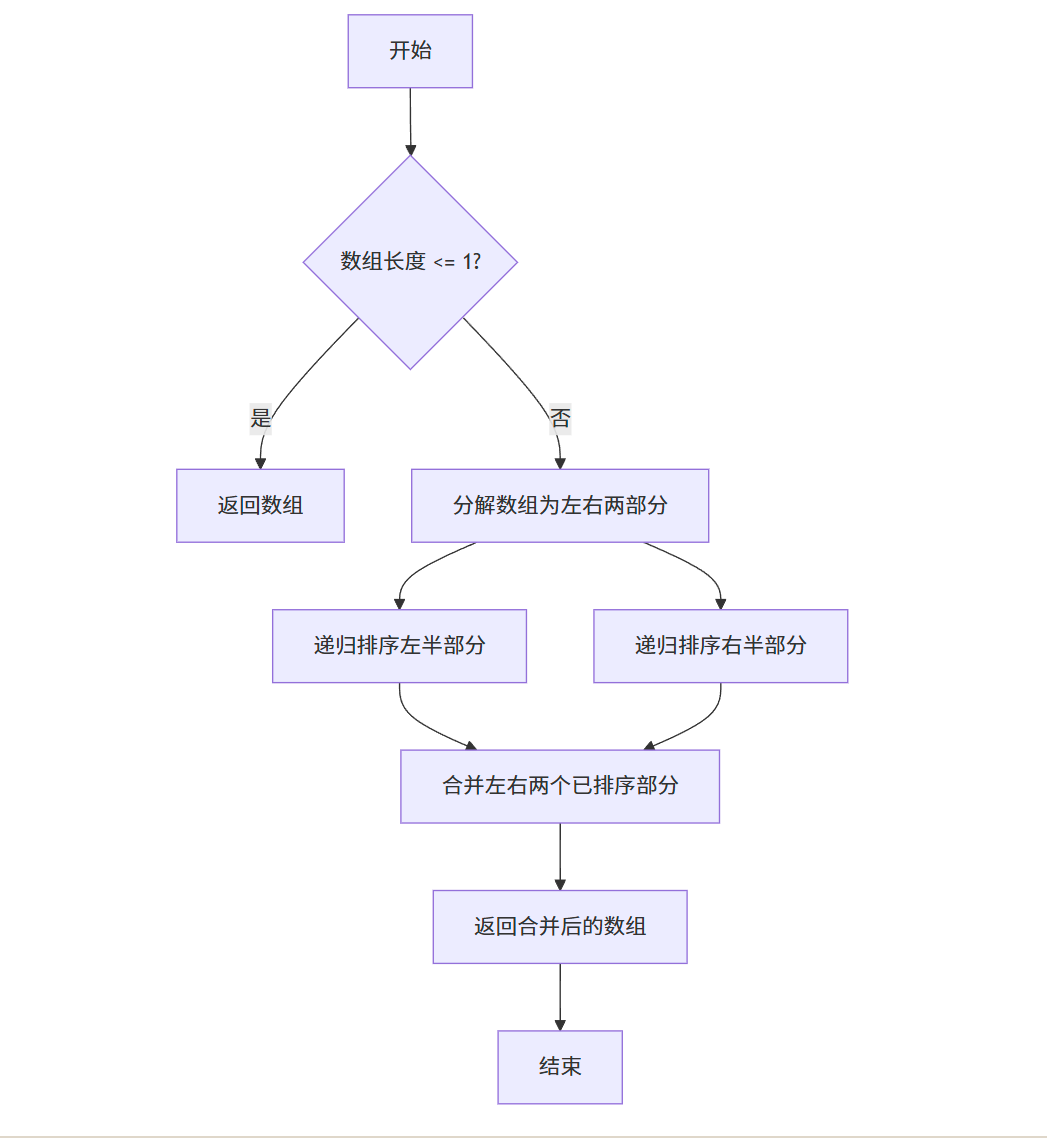
归并排序代码实现(C++)
#include <iostream>
#include <vector>using namespace std;/*** 合并两个已排序的子数组* @param arr 原数组* @param left 左子数组的起始索引* @param mid 左子数组的结束索引,mid+1是右子数组的起始索引* @param right 右子数组的结束索引*/
void merge(vector<int>& arr, int left, int mid, int right) {int n1 = mid - left + 1; // 左子数组的长度int n2 = right - mid; // 右子数组的长度// 创建临时数组vector<int> L(n1), R(n2);// 将数据复制到临时数组for (int i = 0; i < n1; i++)L[i] = arr[left + i];for (int j = 0; j < n2; j++)R[j] = arr[mid + 1 + j];// 合并临时数组回原数组int i = 0, j = 0, k = left;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 复制剩余的元素while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}/*** 归并排序函数* @param arr 待排序的数组* @param left 排序的起始索引* @param right 排序的结束索引*/
void mergeSort(vector<int>& arr, int left, int right) {if (left < right) {// 找到中间点int mid = left + (right - left) / 2;// 递归排序左半部分和右半部分mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);// 合并已排序的两部分merge(arr, left, mid, right);}
}/*** 打印数组* @param arr 要打印的数组*/
void printArray(const vector<int>& arr) {for (int num : arr) {cout << num << " ";}cout << endl;
}int main() {vector<int> arr = {12, 11, 13, 5, 6, 7};cout << "排序前的数组: ";printArray(arr);mergeSort(arr, 0, arr.size() - 1); // 调用归并排序cout << "排序后的数组: ";printArray(arr);return 0;
}
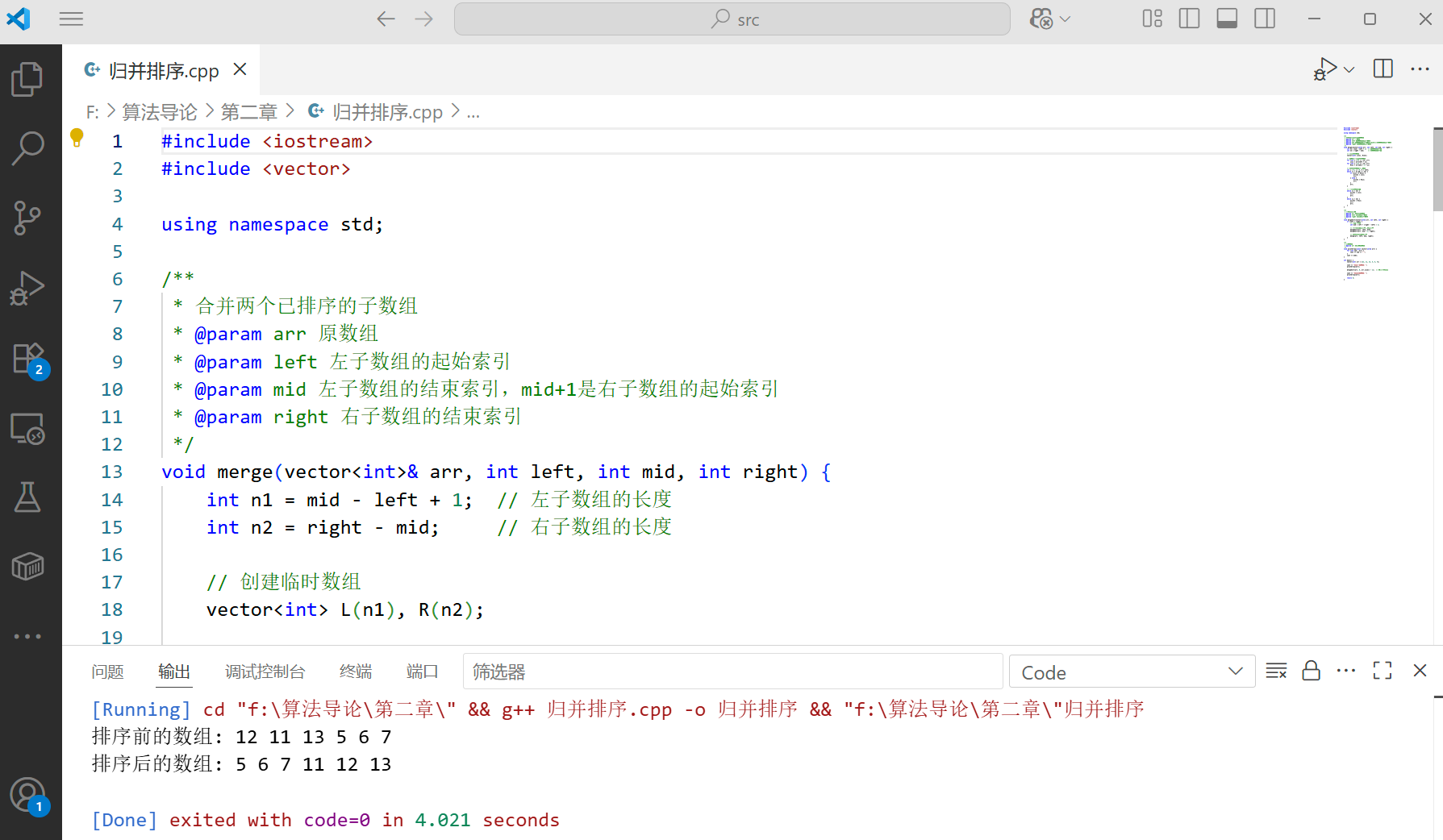
这段代码实现了归并排序的完整功能。mergeSort函数负责分解问题和递归求解,merge函数负责合并两个已排序的子数组。
归并排序综合案例:外部排序
归并排序的一个重要应用是外部排序,即当数据量太大无法全部装入内存时的排序方法。下面是一个简单的外部排序模拟实现:
#include <iostream>
#include <vector>
#include <fstream>
#include <string>
#include <algorithm>using namespace std;// 生成测试数据文件
void generateTestData(const string& filename, int size) {ofstream fout(filename);for (int i = 0; i < size; i++) {fout << rand() % 10000 << endl; // 生成随机数}fout.close();
}// 从文件中读取指定数量的数据
vector<int> readChunk(const string& filename, int start, int count) {vector<int> chunk;ifstream fin(filename);string line;int num, i = 0;while (getline(fin, line) && i < start + count) {if (i >= start) {num = stoi(line);chunk.push_back(num);}i++;}fin.close();return chunk;
}// 将数据块写入临时文件
string writeTempChunk(const vector<int>& chunk, int id) {string filename = "temp_" + to_string(id) + ".txt";ofstream fout(filename);for (int num : chunk) {fout << num << endl;}fout.close();return filename;
}// 归并两个有序文件
string mergeFiles(const string& file1, const string& file2, int id) {ifstream fin1(file1), fin2(file2);string outfile = "temp_" + to_string(id) + ".txt";ofstream fout(outfile);string line1, line2;// 修复:使用good()方法检查流状态bool has1 = getline(fin1, line1).good();bool has2 = getline(fin2, line2).good();int num1, num2;while (has1 && has2) {num1 = stoi(line1);num2 = stoi(line2);if (num1 <= num2) {fout << num1 << endl;// 修复:使用good()方法检查流状态has1 = getline(fin1, line1).good();} else {fout << num2 << endl;// 修复:使用good()方法检查流状态has2 = getline(fin2, line2).good();}}// 写入剩余数据while (has1) {fout << line1 << endl;// 修复:使用good()方法检查流状态has1 = getline(fin1, line1).good();}while (has2) {fout << line2 << endl;// 修复:使用good()方法检查流状态has2 = getline(fin2, line2).good();}fin1.close();fin2.close();fout.close();// 删除临时文件remove(file1.c_str());remove(file2.c_str());return outfile;
}// 外部归并排序
void externalMergeSort(const string& filename, int chunkSize) {// 步骤1: 读取文件并创建有序的数据块vector<string> tempFiles;int chunkId = 0;vector<int> chunk;do {chunk = readChunk(filename, chunkId * chunkSize, chunkSize);if (chunk.empty()) break;// 对数据块进行排序sort(chunk.begin(), chunk.end());// 写入临时文件tempFiles.push_back(writeTempChunk(chunk, chunkId));chunkId++;} while (chunk.size() == chunkSize);// 步骤2: 归并所有临时文件while (tempFiles.size() > 1) {vector<string> newTempFiles;for (size_t i = 0; i < tempFiles.size(); i += 2) {if (i + 1 < tempFiles.size()) {// 归并两个文件newTempFiles.push_back(mergeFiles(tempFiles[i], tempFiles[i+1], chunkId++));} else {// 如果是奇数个文件,最后一个文件直接进入下一轮newTempFiles.push_back(tempFiles[i]);}}tempFiles = newTempFiles;}// 重命名最终文件if (!tempFiles.empty()) {rename(tempFiles[0].c_str(), "sorted_result.txt");}cout << "外部排序完成,结果保存到 sorted_result.txt" << endl;
}int main() {// 生成10000个随机数作为测试数据generateTestData("data.txt", 10000);// 进行外部排序,假设内存只能容纳1000个数据externalMergeSort("data.txt", 1000);return 0;
}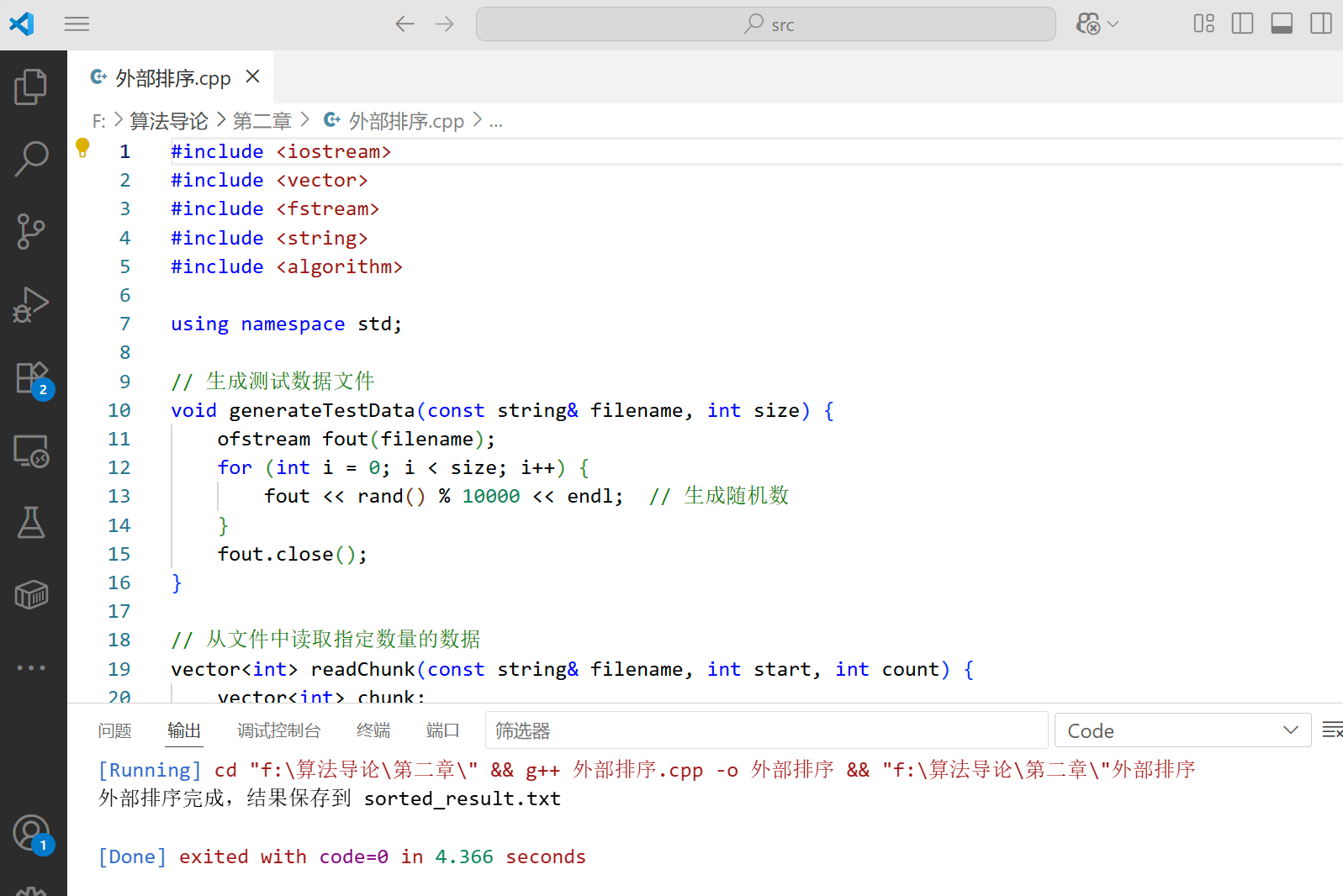
这个案例模拟了外部排序的过程,它将大文件分成多个可装入内存的块,分别排序后再逐步归并,最终得到整个文件的有序版本。这展示了归并排序在处理大规模数据时的优势。
2.3.2 分析分治算法
分治算法的时间复杂度分析通常需要求解递归式。递归式是一个用较小输入的函数值来描述函数的等式或不等式。
递归式的求解方法
求解递归式的常用方法有:
- 代入法:猜测一个解,然后用数学归纳法证明其正确性
- 递归树法:将递归式转换为一棵树,其节点表示不同层次的递归调用产生的代价
- 主方法:用于求解形如 T (n) = aT (n/b) + f (n) 的递归式
主方法
主方法给出了如下递归式的解:
T (n) = aT (n/b) + f (n)
其中:
- a ≥ 1,b > 1 是常数
- f (n) 是一个渐近正函数
- n/b 可以是 floor (n/b) 或 ceil (n/b)
主方法有三种情况:
- 若 f (n) = O (n^log_b (a-ε)) 对某个常数 ε > 0 成立,则 T (n) = Θ(n^log_b a)
- 若 f (n) = Θ(n^log_b a),则 T (n) = Θ(n^log_b a * log n)
- 若 f (n) = Ω(n^log_b (a+ε)) 对某个常数 ε > 0 成立,且对某个常数 c < 1 和所有足够大的 n 有 af (n/b) ≤ cf (n),则 T (n) = Θ(f (n))
归并排序的时间复杂度分析
归并排序的递归式为:
T (n) = 2T (n/2) + Θ(n)
应用主方法:
- a = 2,b = 2,所以 log_b a = log2 2 = 1
- f (n) = Θ(n) = Θ(n^1),符合主方法的第二种情况
因此,归并排序的时间复杂度为 T (n) = Θ(n log n),这在三种情况(最好、最坏、平均)下都是成立的。
分治算法分析案例
下面我们通过一个案例来具体分析分治算法的时间复杂度:
#include <iostream>
#include <vector>
#include <cmath>using namespace std;/*** 用分治法求数组中的最大元素* @param arr 输入数组* @param left 左边界索引* @param right 右边界索引* @return 数组中的最大元素*/
int findMax(const vector<int>& arr, int left, int right) {// 基本情况:如果数组只有一个元素,返回该元素if (left == right) {return arr[left];}// 分解:找到中间点int mid = left + (right - left) / 2;// 解决:递归寻找左右两部分的最大值int maxLeft = findMax(arr, left, mid);int maxRight = findMax(arr, mid + 1, right);// 合并:返回两个最大值中的较大者return max(maxLeft, maxRight);
}/*** 分析分治法求最大值的时间复杂度* T(n) = 2T(n/2) + Θ(1)* 根据主方法,a=2, b=2, log_b a=1, f(n)=Θ(1) = O(n^0)* 符合第一种情况,所以 T(n) = Θ(n^1) = Θ(n)*/
void analyzeTimeComplexity() {cout << "分治法求最大值的时间复杂度分析:" << endl;cout << "递归式:T(n) = 2T(n/2) + Θ(1)" << endl;cout << "其中 a=2, b=2, f(n)=Θ(1)" << endl;cout << "log_b a = log2(2) = 1" << endl;cout << "由于 f(n) = O(n^(1-ε)) 对于 ε=1 成立," << endl;cout << "根据主方法第一种情况,T(n) = Θ(n)" << endl;
}int main() {vector<int> arr = {12, 34, 54, 2, 3};cout << "数组中的最大值是:" << findMax(arr, 0, arr.size() - 1) << endl;analyzeTimeComplexity();return 0;
}
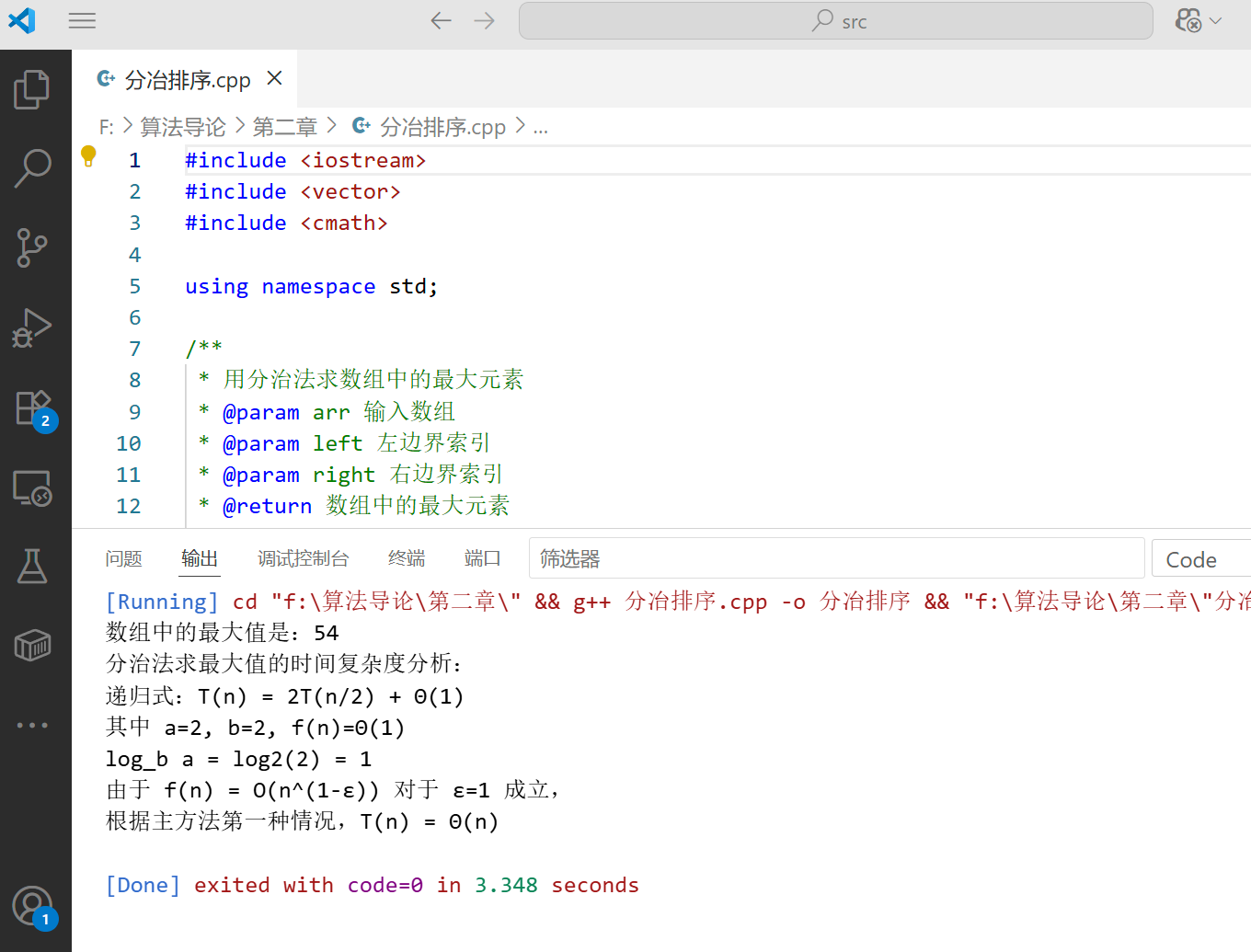
这个案例分析了用分治法求数组最大值的时间复杂度。递归式为 T (n) = 2T (n/2) + Θ(1),根据主方法的第一种情况,我们得出其时间复杂度为 Θ(n)。

思考题
比较插入排序和归并排序:
- 什么情况下插入排序比归并排序更高效?
- 如何优化插入排序使其在实际应用中表现更好?
算法设计:
- 设计一个基于分治法的算法,求一个数组中元素的和。
- 分析该算法的时间复杂度。
算法分析:
- 求解递归式 T (n) = 3T (n/2) + n^2
- 求解递归式 T (n) = T (2n/3) + 1
实践题:
- 实现一个版本的归并排序,当子数组的规模小于某个阈值时,改用插入排序。
- 尝试不同的阈值,观察算法性能的变化。
参考答案提示:
- 当数组规模很小或数组已经基本有序时,插入排序可能更高效,因为它的常数因子较小。可以通过二分查找来优化插入排序中寻找插入位置的步骤。
- 分治法求数组和可以将数组分成两半,分别求和后相加。时间复杂度为 Θ(n)。
- 第一个递归式用主方法第三种情况,解为 Θ(n²);第二个用主方法第一种情况,解为 Θ(log n)。
- 这种混合排序算法结合了两种排序的优点,通常能获得更好的实际性能。最佳阈值通常在 10-20 之间,但也可能因具体实现和数据特征而变化。

本章注记
本章介绍了算法分析的基本框架和两种重要的排序算法:插入排序和归并排序。插入排序的时间复杂度为 O (n²),但实现简单,常数因子小,适合小规模数据或接近有序的数据。归并排序采用分治策略,时间复杂度为 Θ(n log n),适合大规模数据排序。
算法分析是计算机科学的基础技能,大 O 记号和递归式分析是评估算法效率的重要工具。分治法是一种强大的算法设计范式,不仅用于排序,还广泛应用于其他领域,如查找、矩阵乘法、快速傅里叶变换等。
通过本章的学习,我们应该掌握:
- 分析算法时间复杂度的基本方法
- 插入排序和归并排序的原理及实现
- 分治法的基本思想和应用
- 递归式的求解方法,特别是主方法

在实际应用中,选择合适的算法需要考虑问题规模、数据特征和实际运行环境等多种因素。理解不同算法的优缺点和适用场景,是成为一名优秀程序员的重要一步。
希望这篇学习笔记能帮助你更好地理解《算法导论》第 2 章的内容。如果有任何疑问或建议,欢迎在评论区留言讨论!

以上就是《算法导论》第 2 章的全部学习内容。通过理论学习和代码实践相结合的方式,相信大家已经对算法基础有了更深入的理解。算法学习是一个循序渐进的过程,建议大家多动手实现,多思考分析,不断提升自己的算法能力。