洛谷 P3373 【模板】线段树 2- 普及+/提高
题目描述
如题,已知一个数列 aaa,你需要进行下面三种操作:
- 将某区间每一个数乘上 xxx;
- 将某区间每一个数加上 xxx;
- 求出某区间每一个数的和。
输入格式
第一行包含三个整数 n,q,mn,q,mn,q,m,分别表示该数列数字的个数、操作的总个数和模数。
第二行包含 nnn 个用空格分隔的整数,其中第 iii 个数字表示数列第 iii 项的初始值 aia_iai。
接下来 qqq 行每行包含若干个整数,表示一个操作,具体如下:
操作 111: 格式:1 x y k 含义:将区间 [x,y][x,y][x,y] 内每个数乘上 kkk。
操作 222: 格式:2 x y k 含义:将区间 [x,y][x,y][x,y] 内每个数加上 kkk。
操作 333: 格式:3 x y 含义:输出区间 [x,y][x,y][x,y] 内每个数的和对 mmm 取模所得的结果。
输出格式
输出包含若干行整数,即为所有操作 333 的结果。
输入输出样例 #1
输入 #1
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
输出 #1
17
2
说明/提示
【数据范围】
对于 30%30\%30% 的数据:n≤8n \le 8n≤8,q≤10q \le 10q≤10。
对于 70%70\%70% 的数据:$n \le 10^3 ,,,q \le 10^4$。
对于 100%100\%100% 的数据:1≤n≤1051 \le n \le 10^51≤n≤105,1≤q≤105,1≤ai,k≤1041 \le q \le 10^5,1\le a_i,k\le 10^41≤q≤105,1≤ai,k≤104。
除样例外,m=571373m = 571373m=571373。
(数据已经过加强 _)
样例说明:
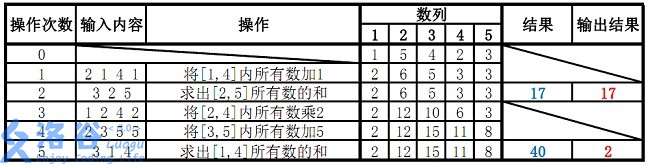
故输出应为 171717、222(40 mod 38=240 \bmod 38 = 240mod38=2)。
solution
对于乘法操作,sum add mul 都需要乘
对于加法操作,sum mul 都要加
代码
#include <sstream>
#include "iostream"
#include "cmath"
#include "vector"
#include "algorithm"using namespace std;
const int N = 1e5 + 5;int n, mod;
long long b[N];struct node {long long sum, add, mul;
} a[4 * N];// 将父节点的 tag 信息向下分摊
void push_down(int rt, int l, int r) {// 先算乘法、再算加法, 因为乘法影响加法,加法不影响乘法int m = r + l >> 1;a[rt * 2].sum = (a[rt * 2].sum * a[rt].mul + a[rt].add * (m + 1 - l)) % mod;a[rt * 2 + 1].sum = (a[rt * 2 + 1].sum * a[rt].mul + a[rt].add * (r - m)) % mod;a[rt * 2].add = (a[rt * 2].add * a[rt].mul + a[rt].add) % mod;a[rt * 2 + 1].add = (a[rt * 2 + 1].add * a[rt].mul + a[rt].add) % mod;a[rt * 2].mul = (a[rt * 2].mul * a[rt].mul) % mod;a[rt * 2 + 1].mul = (a[rt * 2 + 1].mul * a[rt].mul) % mod;a[rt].add = 0;a[rt].mul = 1;
}void push_up(int rt) {a[rt].sum = (a[rt * 2].sum + a[rt * 2 + 1].sum) % mod;
}void build(int rt, int l, int r) {a[rt].add = 0, a[rt].mul = 1;if (l == r) {a[rt].sum = b[l];return;}int m = l + r >> 1;build(rt * 2, l, m);build(rt * 2 + 1, m + 1, r);push_up(rt);
}void update_mul(int rt, int l, int r, int L, int R, int mul) { // l, r 是 rt管理的区间, L R是修改的区间, k 是修改的量// 整个区间都要改变if (L <= l && r <= R) {a[rt].sum = (a[rt].sum * mul) % mod;a[rt].add = (a[rt].add * mul) % mod;a[rt].mul = (a[rt].mul * mul) % mod;return;}push_down(rt, l, r); // tag 向下传递int m = l + r >> 1;if (L <= m) update_mul(rt * 2, l, m, L, R, mul);if (R > m) update_mul(rt * 2 + 1, m + 1, r, L, R, mul);push_up(rt); // sum 向上汇总
}void update_add(int rt, int l, int r, int L, int R, int add) { // l, r 是 rt管理的区间, L R是修改的区间, k 是修改的量// 整个区间都要改变if (L <= l && r <= R) {a[rt].sum = (a[rt].sum + (r - l + 1) * add) % mod;a[rt].add = (a[rt].add + add) % mod;return;}push_down(rt, l, r); // tag 向下传递int m = l + r >> 1;if (L <= m) update_add(rt * 2, l, m, L, R, add);if (R > m) update_add(rt * 2 + 1, m + 1, r, L, R, add);push_up(rt); // sum 向上汇总
}long long query(int rt, int l, int r, int L, int R) {// 整个区间都要if (L <= l && r <= R) {return a[rt].sum;}push_down(rt, l, r);int m = l + r >> 1;long long s = 0;if (L <= m) s += query(rt * 2, l, m, L, R);if (R > m) s += query(rt * 2 + 1, m + 1, r, L, R);return s % mod;
}int main() {int m;cin >> n >> m >> mod;for (int i = 1; i <= n; i++) cin >> b[i];build(1, 1, n);for (int i = 0; i < m; i++) {int op, l, r, k;cin >> op >> l >> r;if (op == 1) {cin >> k;update_mul(1, 1, n, l, r, k);} else if (op == 2) {cin >> k;update_add(1, 1, n, l, r, k);} else {cout << query(1, 1, n, l, r) << endl;}}
}
结果

