当前位置：首页 > news >正文

05 基于sklearn的机械学习-梯度下降（下）

news 2025/8/5 9:58:49

sklearn梯度下降

批量梯度下降（BGD, Batch Gradient Descent）

随机梯度下降（SGD, Stochastic Gradient Descent）

小批量梯度下降（MBGD, Mini-Batch Gradient Descent）

sklearn梯度下降

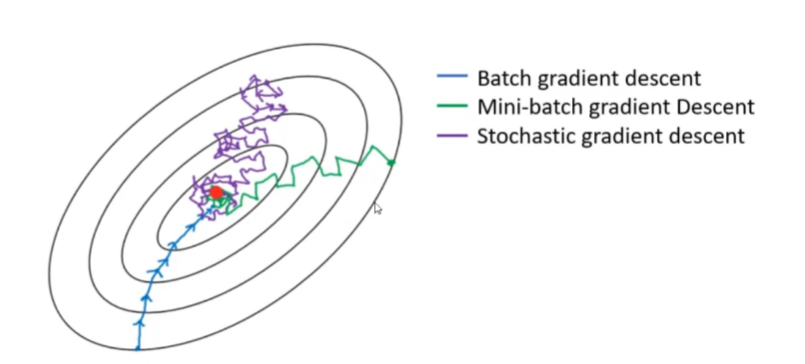
梯度下降是机器学习中常用的优化算法，用于最小化损失函数。根据每次迭代使用的样本数量，可分为三种常见变体：批量梯度下降（BGD）、小批量梯度下降（MBGD）和随机梯度下降（SGD）。

批量梯度下降BGD(Batch Gradient Descent)

小批量梯度下降MBGD(Mini-BatchGradient Descent)

随机梯度下降SGD(Stochastic Gradient Descent)。

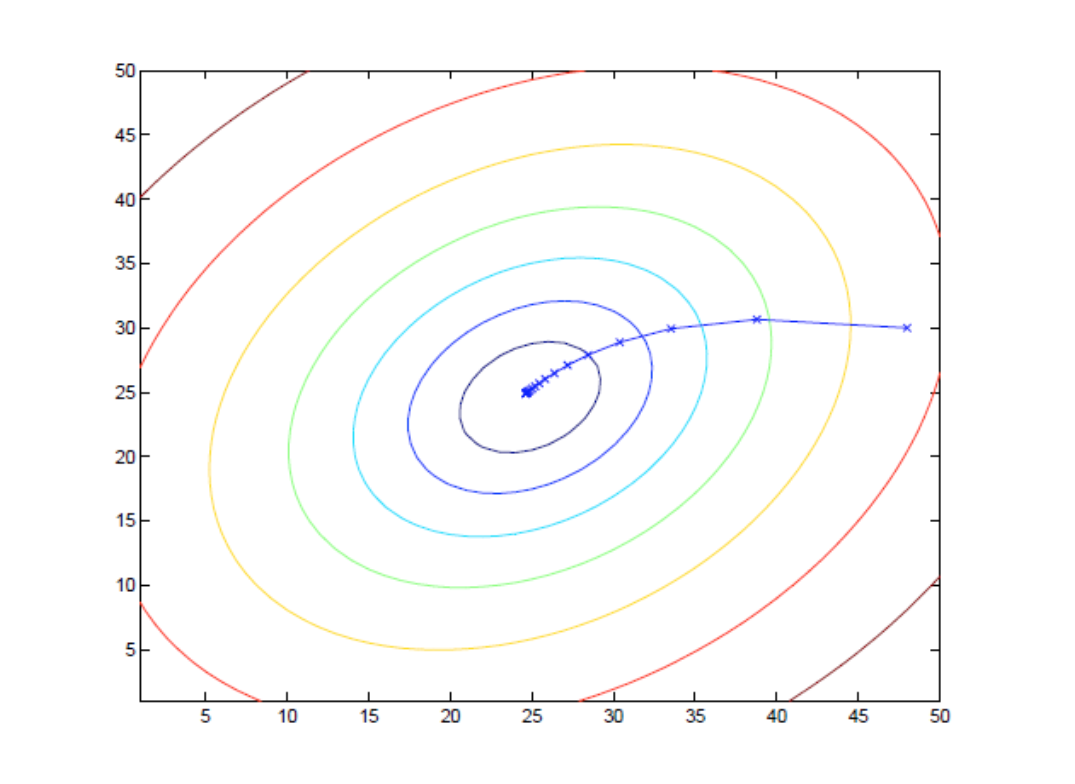
批量梯度下降（BGD, Batch Gradient Descent）

三种主要类型的梯度下降 - 幽魂倪 - 博客园

原理：每次迭代使用全部训练样本计算梯度并更新参数。
优点：梯度估计准确，收敛稳定，可得到全局最优解。
缺点：计算成本高，尤其在大数据集上训练速度慢，无法在线学习（实时更新）。

假设我们有一个包含 ( m ) 个训练样本的数据集 $\{(x^{(i)}, y^{(i)})\}_{i=1}^{m}$ ，其中 $x^{(i)}$ 是输入特征，是对应 $y^{(i)})$ 的标签。我们的目标是最小化损失函数 $J(\theta)$ 相对于模型参数 $\theta$ 的值。

损失函数可以定义为： $J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$

其中 $h_\theta(x^{(i)})$ 是模型对第 i 个样本的预测输出。

批量梯度下降的更新规则为： $\theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m}$ $(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)}$ 对于 j = 0, 1, $\ldots$ n （其中 n 是特征的数量），并且 $\alpha$ 是学习率。

随机梯度下降（SGD, Stochastic Gradient Descent）

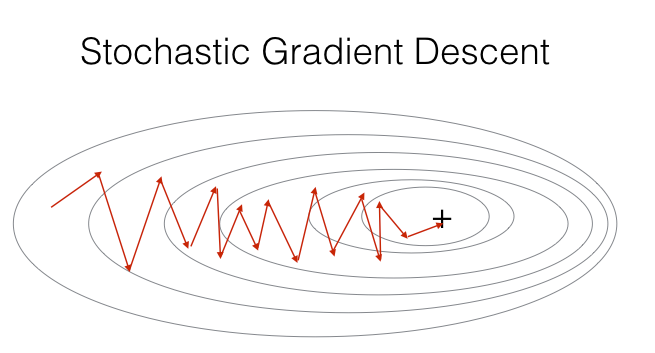
原理：每次迭代随机选择单个样本计算梯度并更新参数。
优点：训练速度快，适合大数据集，支持在线学习。
缺点：梯度波动大，收敛路径曲折，可能在最优解附近震荡。

梯度下降法 - youngliu91 - 博客园

基本步骤

初始化参数: $J(\theta)$
- 选择一个初始点作为参数向量 \theta的初始值。
选择样本:
- 随机选取一个训练样本 ( $x^{(i)}$ , $y^{(i)})$ 。
计算梯度:
- 使用所选样本 ( $x^{(i)}, y^{(i)}$ )来近似计算损失函数的梯度 $\nabla J(\theta)$ 。
更新参数:
- 根据梯度的方向来更新参数 $\theta$ 。更新公式为： $\theta := \theta - \alpha \cdot \nabla J(\theta)$
- 其中 $\theta$ 是学习率，决定了每次迭代时参数更新的步长。
重复步骤 2 到 4:
- 对所有的训练样本重复此过程，直到完成一个完整的 epoch（即所有样本都被访问过一次）。
重复多个 epoch:
- 重复上述过程，直到满足某个停止条件，比如达到最大迭代次数或者梯度足够小。
输出结果:
- 输出最小化损失函数后的最优参数 $\theta$ 。

假设我们有一个包含 (m) 个样本的数据集 $\{(x^{(i)}, y^{(i)})\}_{i=1}^m$ ，其中 $x^{(i)}$ 是第 i 个样本的特征向量， $y^{(i)}$ 是对应的标签。对于线性回归问题，损失函数 $J(\theta)$ 可以定义为均方误差 (Mean Squared Error, MSE)：

$J(\theta) = \frac{1}{2}(h_\theta(x^{(i)}) - y^{(i)})^2$

其中 $h_\theta(x^{(i)}) = \theta^T x^{(i)}$ 是模型对第 i个样本的预测值。

梯度 $\nabla J(\theta)$ 对于每个参数 \theta_j 的偏导数可以表示为：

$\frac{\partial J(\theta)}{\partial \theta_j} = (h_\theta(x^{(i)}) - y^{(i)})x_j^{(i)}$

更新规则

参数 $\theta$ 的更新规则为： $\theta_j := \theta_j - \alpha \cdot \frac{\partial J(\theta)}{\partial \theta_j}$

优点

训练速度快：每次迭代仅处理 1 个样本，适合超大规模数据集。
支持在线学习：新样本可随时加入训练，实时更新模型。
有机会跳出局部最优（梯度随机性带来的 “抖动”）。

缺点

梯度波动大：单个样本的梯度可能与真实梯度偏差大，导致收敛路径曲折。
难以稳定收敛：可能在最优解附近震荡，而非精确收敛到最小值。

适用场景

大规模数据集（如百万级样本）。
在线学习场景（如实时推荐、动态数据流）。

API

sklearn.linear_model.SGDRegressor()

from sklearn.linear_model import SGDRegressor
model = SGDRegressor(loss='squared_error',      # 损失函数（默认MSE）penalty='l2',              # 正则化类型：'l1', 'l2', 'elasticnet'alpha=0.0001,              # 正则化强度（默认较弱）l1_ratio=0.15,            # ElasticNet混合比例（仅penalty='elasticnet'时生效）max_iter=1000,             # 最大迭代次数（实际是epoch数）tol=1e-3,                  # 早停阈值（损失变化<tol时停止）learning_rate='invscaling', # 学习率调度策略：'constant', 'optimal', 'invscaling'eta0=0.01,                 # 初始学习率（learning_rate非'optimal'时生效）power_t=0.25,              # invscaling调度指数：η = η0 / t^power_tearly_stopping=False,      # 是否用验证集早停validation_fraction=0.1,   # 早停验证集比例random_state=None,         # 随机种子warm_start=False           # 是否热启动（复用上次训练结果）
)

属性:  
coef_ 回归后的权重系数
intercept_ 偏置

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDRegressor,LinearRegression
from sklearn.metrics import mean_squared_error

# 加载数据集
housing = fetch_california_housing()
x,y = fetch_california_housing(return_X_y=True,data_home='../src')
print(x.shape)
print(housing.feature_names)
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=0)

# 数据预处理
scaler = StandardScaler()
scaler.fit(x_train)
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

# 创建模型
model = SGDRegressor(loss='squared_error',learning_rate='constant',eta0=0.01,fit_intercept=True, max_iter=1000,shuffle=True)
# 训练模型
model.fit(x_train,y_train)
'''
1. 初始化w
2. 构建损失函数，计算导函数
3. 计算当前梯度
4. 更新w
'''
print('w:',model.coef_)
print('b:',model.intercept_)

# 模型评估
y_hat = model.predict(x_test)
print('预测值:',y_hat)
print('真实值:',y_test)
print('均方误差:',mean_squared_error(y_test,y_hat))

小批量梯度下降（MBGD, Mini-Batch Gradient Descent）

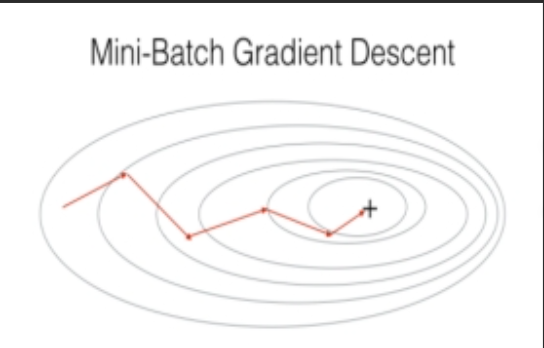
原理：每次迭代使用一小部分样本（批量） 计算梯度并更新参数（通常批量大小为 16~256）。
优点：平衡了 BGD 和 SGD 的优缺点，梯度估计较稳定，训练效率高。
缺点：需要额外选择批量大小超参数。

假设我们有一个包含 ( m ) 个训练样本的数据集 $\{(x^{(i)}, y^{(i)})\}_{i=1}^{m}$ ，其中 $x^{(i)}$ 是输入特征， $y^{(i)}$ 是对应的标签。我们将数据集划分为多个小批量，每个小批量包含 ( b ) 个样本，其中 ( b ) 称为批量大小（batch size），通常 ( b ) 远小于 ( m )。

损失函数可以定义为： $J(\theta) = \frac{1}{2b} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$

其中 $h_\theta(x^{(i)})$ 是模型对第 i 个样本的预测输出。

小批量梯度下降的更新规则为： $\theta_j := \theta_j - \alpha \frac{1}{b} \sum_{i \in B}$ $(h_\theta(x^{(i)}) - y^{(i)}) \cdot x_j^{(i)}$ 对于 j = 0, 1, ... n （其中 n 是特征的数量），并且 $\alpha$ 是学习率， B 表示当前小批量中的样本索引集合。