lumerical——锥形波导偏振转换
一、使用 FDE 进行初始设计
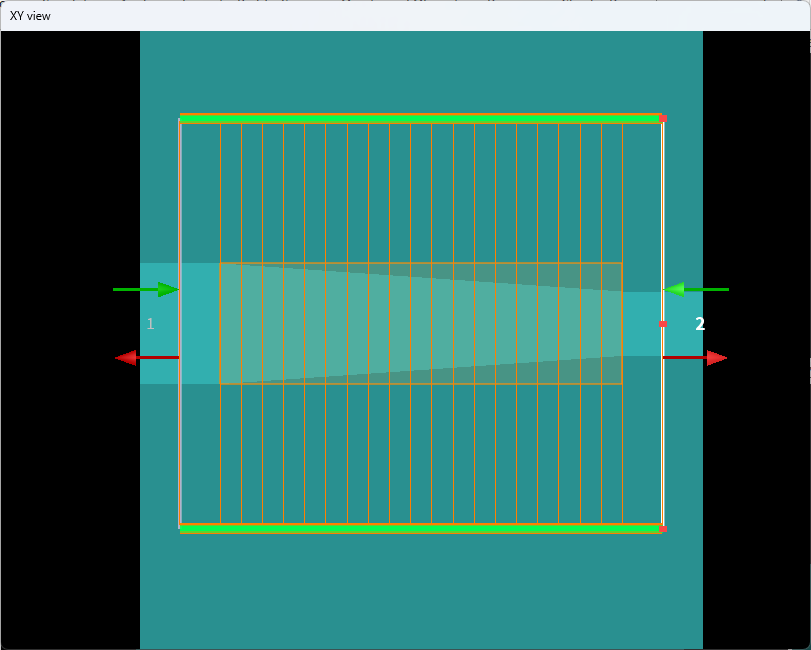
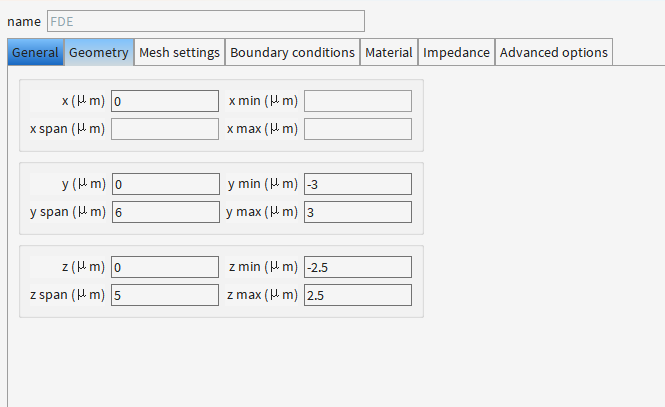
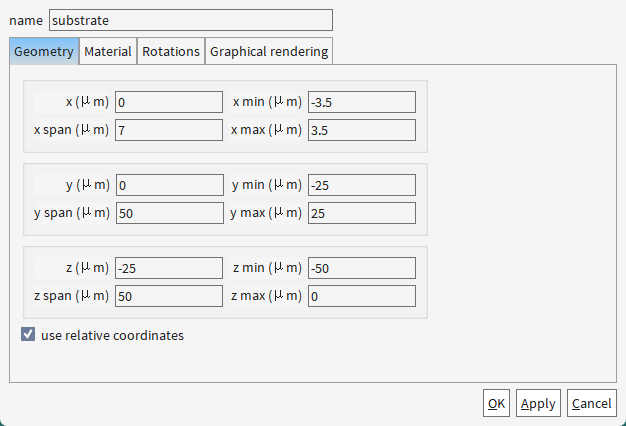
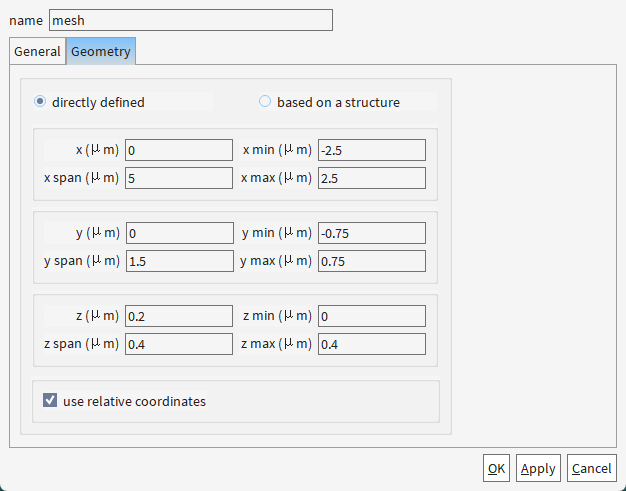
1.1 创建结构
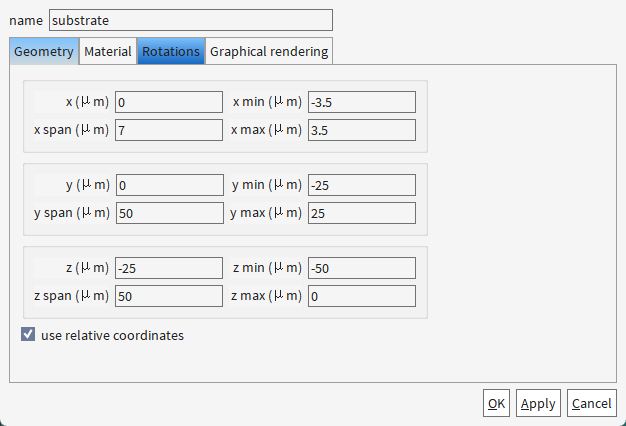
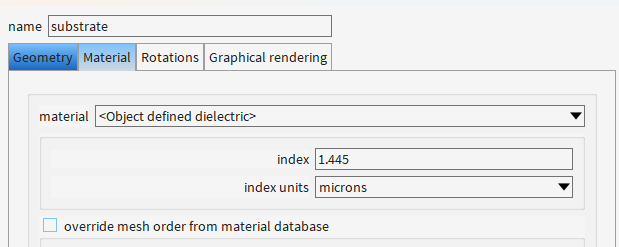
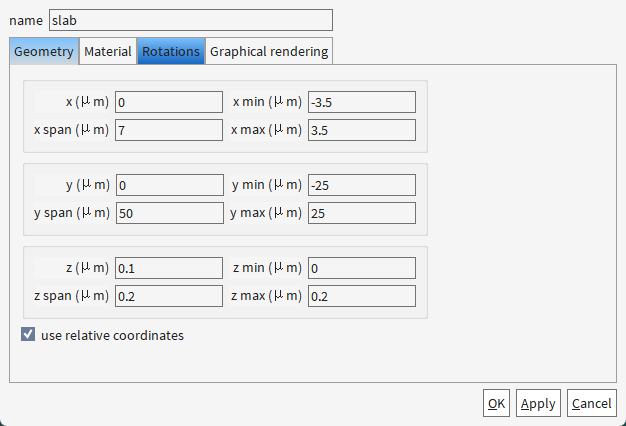
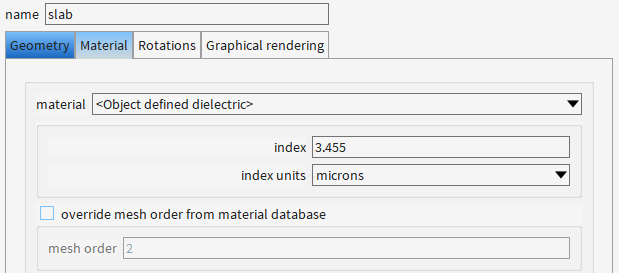
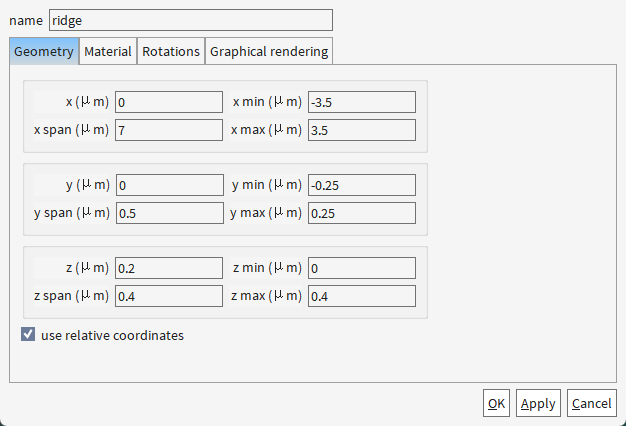
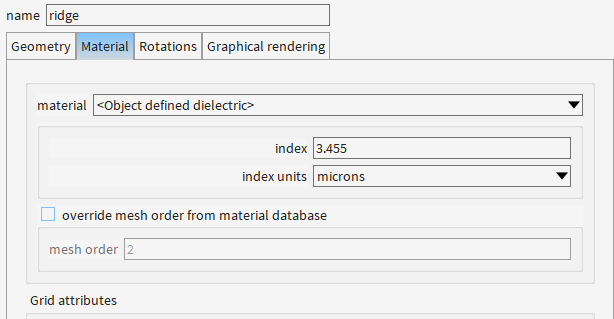
为啥ridge的z方向不直接从0.2开始,还是从0开始,和slab重合了呢?
1. 确保结构连续性(避免数值误差)
物理需求:锥形波导的ridge需要与下层slab无缝连接,重合区域(Z=0-0.2 μm)保证界面处材料属性平滑过渡。
仿真稳定性:若ridge从Z=0.2 μm开始,软件可能因网格不连续在交界处引入虚假反射或模式泄漏。
2. 材料定义的完整性
slab层(Z=0-0.2 μm):通常定义为衬底材料(如SiO₂)
ridge层(Z=0-0.4 μm):
下部(Z=0-0.2 μm)与slab重叠 → 自动继承slab材料属性
上部(Z=0.2-0.4 μm)为波导核心(如Si)
优势:通过重叠区域自动实现材料堆叠,无需手动设置界面。
3. 网格剖分优化
重合区域:强制网格在Z=0.2 μm界面处对齐,避免因独立划分网格导致的模式场畸变
4. 偏振转换的特殊要求
锥形波导偏振转换设计更需注意:
模式重叠积分:TE-TM模式转换效率对ridge/slab界面处的场分布极其敏感,重合区域可保证模式计算准确性。
渐变过渡:若ridge不从Z=0开始,锥形区域的侧向斜率(如y方向)可能因网格突变引入虚假双折射效应。
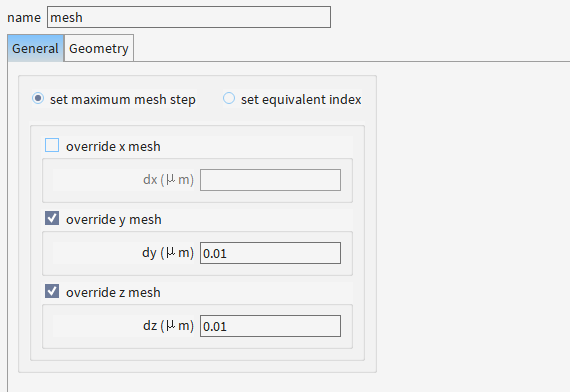
1.2 添加FDE
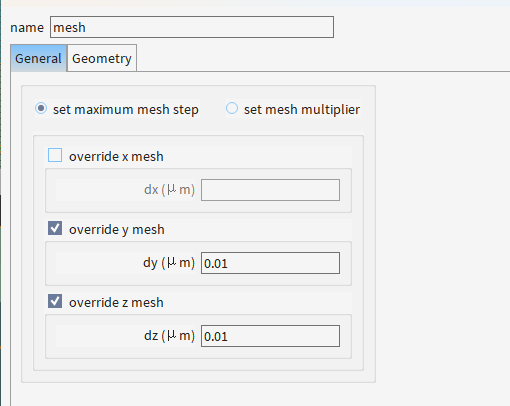
为啥仅覆盖dy/dz(Y/Z方向)而不覆盖dx(X方向)
- Y-Z截面模式场的精确解析:
- TE/TM模的电场分布(如Ey和Ez分量)需亚纳米级网格(0.01 μm)才能捕捉模式耦合细节。
- 特别是波导边缘的倏逝场(对偏振敏感),需加密Y/Z网格。
- X方向的渐变特性:
锥形波导的斜率通常较小(如0.1°~1°),X方向的光场变化缓慢,默认网格已足够描述相位累积。
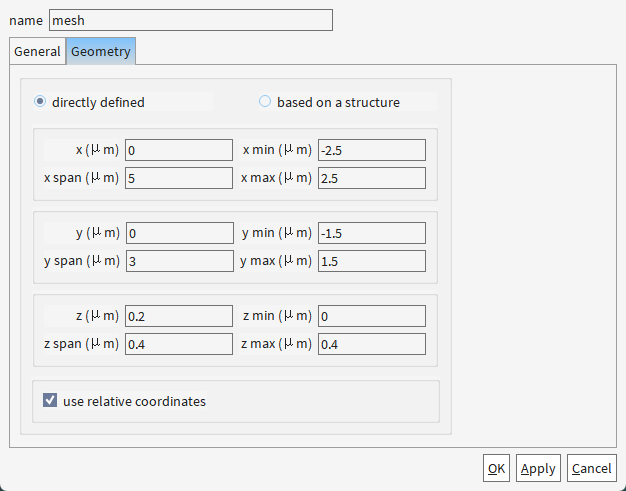
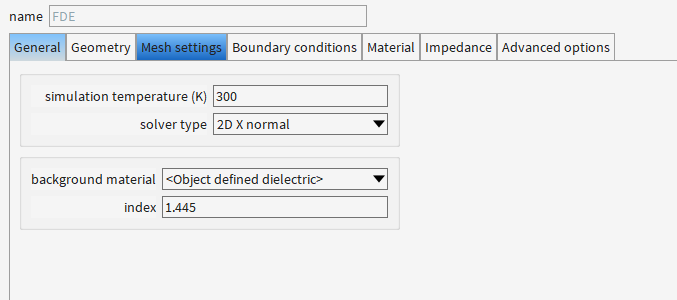
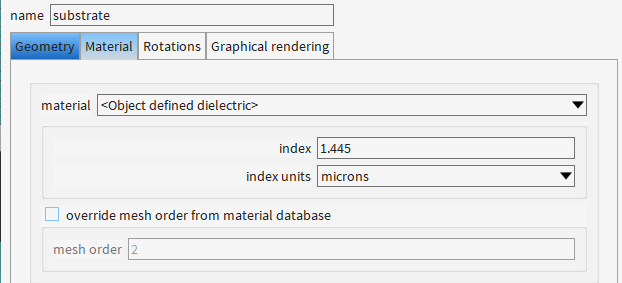
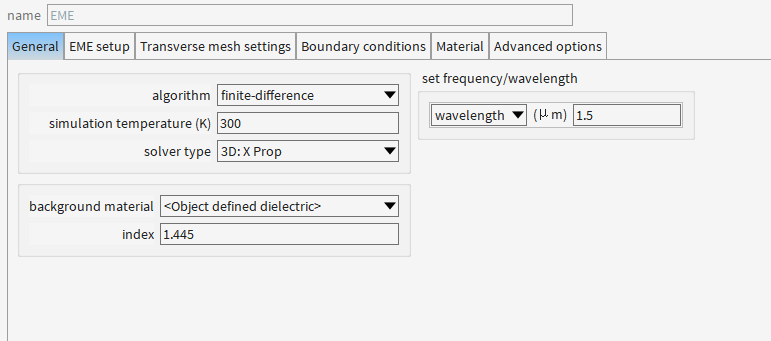
为啥要设置背景材料折射率为1.445?
(1) 模拟实际封装环境
典型场景:锥形波导通常封装在二氧化硅(SiO₂)或聚合物(如UV胶)中,其折射率约为1.44-1.46。
本例中的1.445:精确匹配SiO₂在1550 nm波段的折射率(若为其他材料需调整)。
(2) 影响偏振转换效率
倏逝场约束:背景介质折射率决定波导外光场的衰减速度,影响TE/TM模的耦合强度。
若背景折射率过高(如>1.5),会导致模式泄露,降低转换效率。
若过低(如1.0,空气),会增强模式约束但可能引入非物理反射。
双折射调控:背景与波导核心(如Si,n≈3.48)的折射率差影响模式的有效折射率差(Δneff),进而调控偏振转换速率。
为啥多数案例不显式设置?
| 情况分类 | 是否设置背景折射率 | 原因 |
|---|---|---|
| 简单波导仿真 | 通常忽略 | 默认空气(n=1.0)已足够,且对基模特性影响小 |
| 偏振转换器件 | 必须精确设置 | 转换效率对背景介质的介电常数极其敏感(误差5%可导致效率偏差>20% |
1.3 运行脚本
clear; cleardcard;
waveguide_width = linspace(3e-6,0.5e-6,21); # 波导宽度从3μm渐变到0.5μm,分21个点neff1 = matrix(length(waveguide_width)); # 存储TE0模的neff
neff2 = matrix(length(waveguide_width)); # 存储TE1模的neff
neff3 = matrix(length(waveguide_width)); # 存储TE2模的neff
neff4 = matrix(length(waveguide_width)); # 存储TE3模的neff
neff5 = matrix(length(waveguide_width)); # 存储TM0模的neffslab_neff = 2.754047; # 参考值:无脊波导(仅slab)的neff,用于归一化,突出脊波导的导模特性。
# 每次循环调整波导宽度并重新计算模式(findmodes)
for (i=1:length(waveguide_width)){# set geometryswitchtolayout;setnamed('ridge','y span',waveguide_width(i)); # 设置当前宽度findmodes;# store top 5 modes for largest waveguide width# since the mode order may change for different width # 在最大宽度(3μm)时人工标记模式顺序(TE0/TE1/TE2/TE3/TM0),避免后续因模式阶数跳变导致数据错位if (i==1){copydcard('mode1','TE0'); # 将第一个模式标记为TE0copydcard('mode2','TE1'); # 第二个模式标记为TE1copydcard('mode3','TE2'); # 第三个模式标记为TE2copydcard('mode4','TE3'); # 第四个模式标记为TE3copydcard('mode5','TM0'); # 第五个模式标记为TM0}# store neff for modes at other waveguide width# bestoverlap('TE0'):通过场重叠积分找到当前宽度下与基准TE0模最匹配的模式# real(getdata(...)):获取有效折射率的实部(忽略损耗虚部)# -slab_neff:计算相对于slab的折射率增量(突出波导的导模特性)neff1(i) = real(getdata(bestoverlap('TE0'),'neff'))-slab_neff; # 计算TE0模的Δneffneff2(i) = real(getdata(bestoverlap('TE1'),'neff'))-slab_neff; # 计算TE1模的Δneffneff3(i) = real(getdata(bestoverlap('TE2'),'neff'))-slab_neff; # 计算TE2模的Δneffneff4(i) = real(getdata(bestoverlap('TE3'),'neff'))-slab_neff; # 计算TE3模的Δneffneff5(i) = real(getdata(bestoverlap('TM0'),'neff'))-slab_neff; # 计算TM0模的Δneff# 当波导宽度减小,高阶模(如TE2/TE3)可能截止(neff接近slab_neff),需剔除无效数据if (neff3(i) == neff1(i)){neff3(i) = 0;} # 若TE2与TE0重合,置零if (neff4(i) == neff2(i)){neff4(i) = 0;} # 若TE3与TE1重合,置零
}# plot in normalized units
# 结果可视化
plot(waveguide_width*1e6,neff1,neff2,neff3,neff4,neff5,'waveguide width (um)','delta_neff');
setplot('y min',0); setplot('y max',max(neff1));
legend('TE0','TE1','TE2','TE3','TM0');
注:宽度变化由脚本动态控制(Y span从3 μm→0.5 μm),FDE面板仅设置局部截面的求解条件
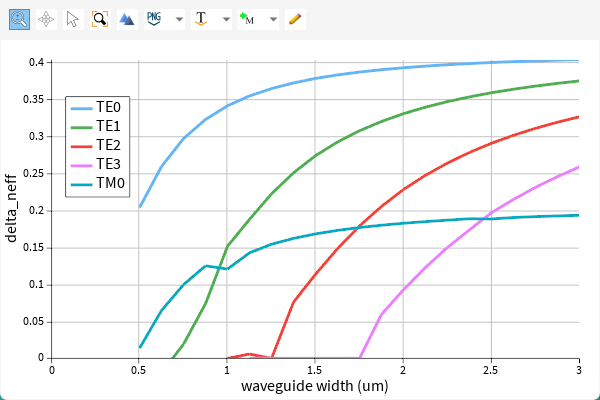
结果分析:
| 模式 | 变化趋势 | 物理意义 |
|---|---|---|
| TE0 | 随宽度增加非线性上升 | 波导对基模的约束力增强,但受限于材料折射率差,上升速率渐缓 |
| TM0 | 近似线性增长 | 对宽度变化不敏感,适合作为稳定输出偏振态 |
| TE1-3 | 窄区(<1 μm)急剧截止 | 高阶模在窄波导中无法维持,能量泄漏到slab层 |
(1) 波导宽度与模式控制能力
TE0模:始终具有最高的Δneff(0.05~0.35),表明其对波导宽度的变化最敏感,适合作为偏振转换的主模式。
TM0模:Δneff变化平缓(0~0.15),说明其与slab模式的耦合较弱,需更长的锥形区域实现TE→TM转换。
高阶模(TE1/TE2/TE3):在宽度<1.5 μm时迅速截止(Δneff≈0),避免多模干扰。
(2) 关键设计参数
最优宽度范围:1.5~2 μm时,TE0与TM0的Δneff差值适中(约0.15),可实现高效偏振转换。
避免区域:宽度>2.5 μm时,高阶模(TE1/TE2)被激发,可能引入串扰。
通过精确控制波导宽度,可调控TE/TM模的有效折射率差,实现高效偏振转换,同时需规避高阶模干扰区域。
二、使用 EME 进行长度扫描
从FDE的结果我们选择 1.5um 和 0.8um 作为波导输入和输出的宽度,原因如下:
(1) 输入宽度1.5 μm
优势:
TE0(0.37)与TM0(0.18)的强耦合(Δneff=0.19)。
高阶模(TE1=0.28)与TE0的Δneff=0.09,需通过锥形斜率抑制其激发。
模式 | 纵坐标neff值 | 结论 |
|---|---|---|
TE0 | 0.37 | 实际应为0.37(图表清晰显示) |
TM0 | 0.18 | 实际为0.18 |
TE1 | 0.28 | 高阶模存在但能量较低 |
TE2 | 0.15 | 实际为0.15 |
TE3 | ≈0 | 基本截止 |
(2) 输出宽度0.8 μm
单模保障:TE0(0.32)主导。
| 模式 | neff值 | 物理意义 |
|---|---|---|
| TE0 | ≈0.32 | 波导仍能较强约束TE0模 |
| TM0 | ≈0.18 | TM0模接近截止(能量泄漏) |
| TE1 | ≈0.17 | 高阶模即将截止(neff<0.2) |
| TE2 | ≈0.05 | 基本截止(能量几乎不约束) |
| TE3 | ≈0 | 完全截止 |
2.1 创建结构
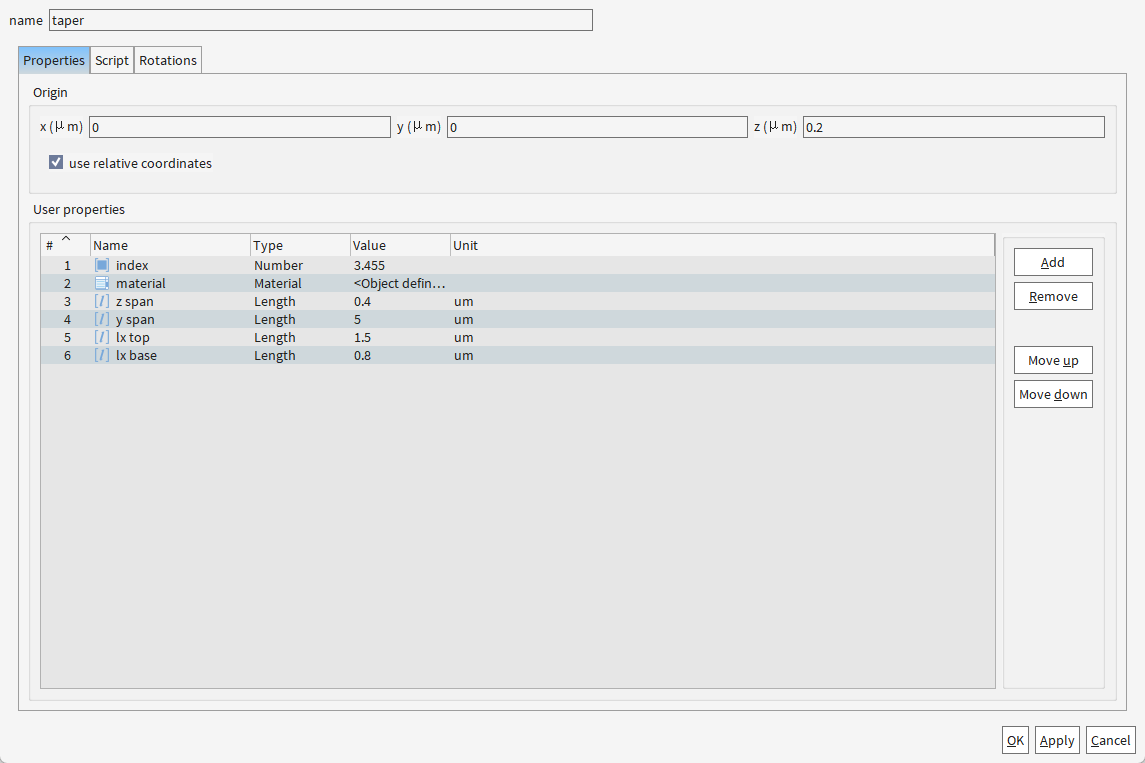
deleteall;
##############################################
# Isosceles trapezoid
# An extruded isosceles trapezoid that is symmetric
# about its vertical center line.
#
# Input properties
# index: index of refraction for dielectric
# material: material of object
# z span: thickness of extrusion
# y span: vertical length of trapezoid
# lx top: top length of trapezoid
# lx base: base length of the trapezoid
#
# Tags: polygon extrusion isosceles trapezoid
#
# Copyright 2010 Lumerical Solutions Inc
##############################################
# simplify variable names by removing spaces
z_span = %z span%;
y_span = %y span%;
lx_top = %lx top%;
lx_base = %lx base%;V=matrix(4,2);
#[x,y] points
V(1,1:2)=[-lx_base/2,-y_span/2];
V(2,1:2)=[-lx_top/2,y_span/2];
V(3,1:2)=[lx_top/2,y_span/2];
V(4,1:2)=[lx_base/2,-y_span/2];addpoly;set("x",0);set("y",0);set("z",0);set("z span",z_span);set("vertices",V);set("material",material);if(get("material")=="<Object defined dielectric>") { set("index",index); } 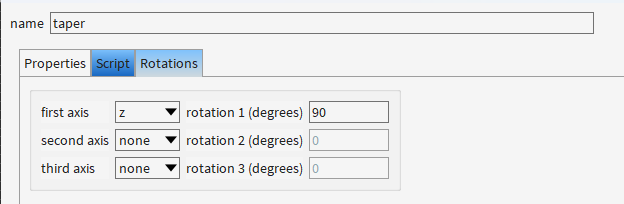
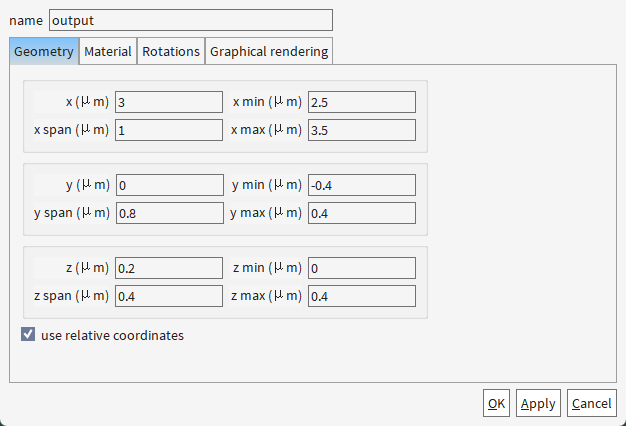
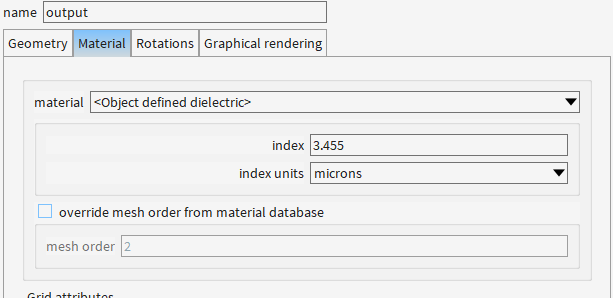
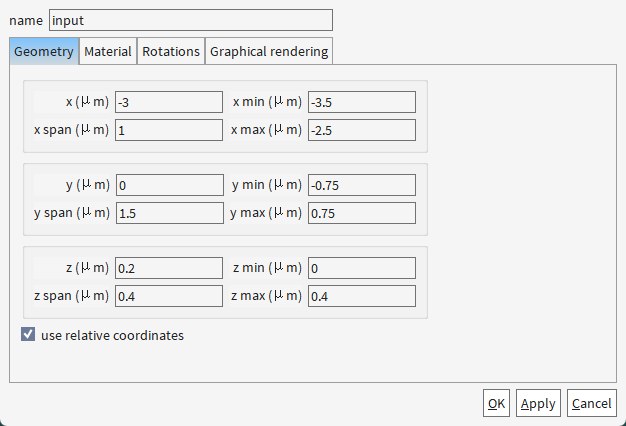
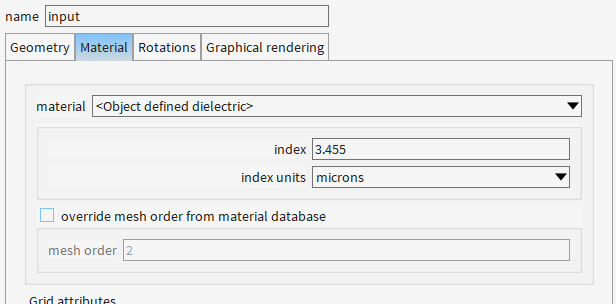
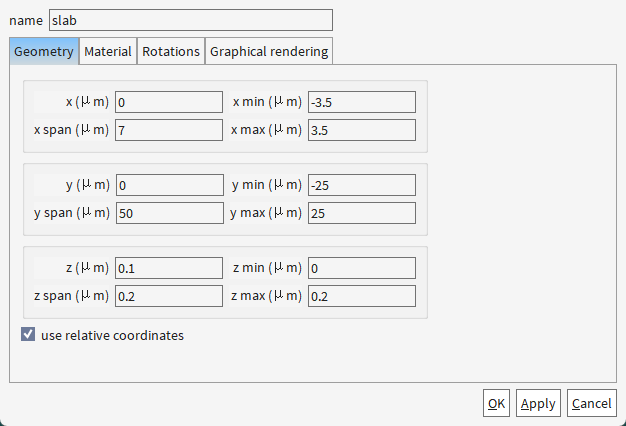
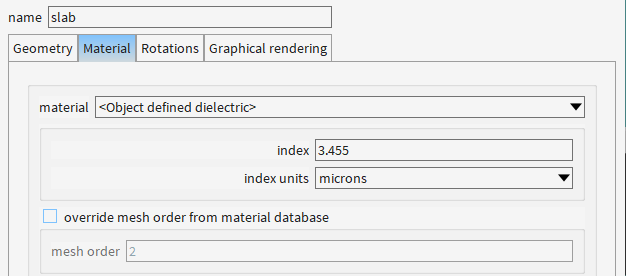
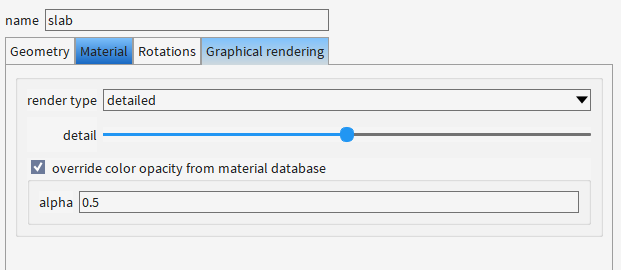
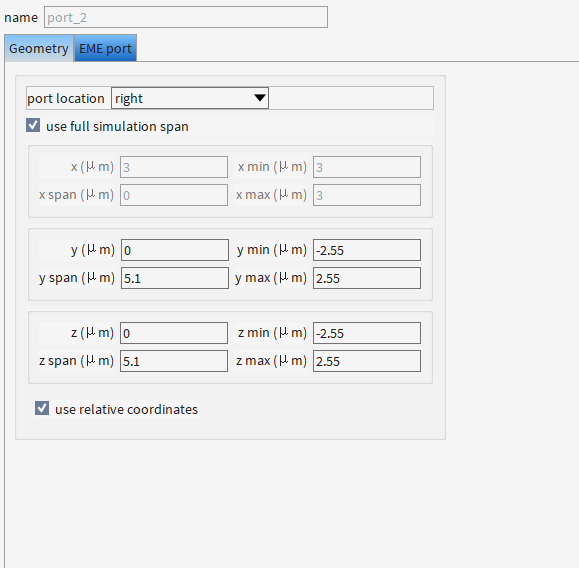
2.2 添加EME
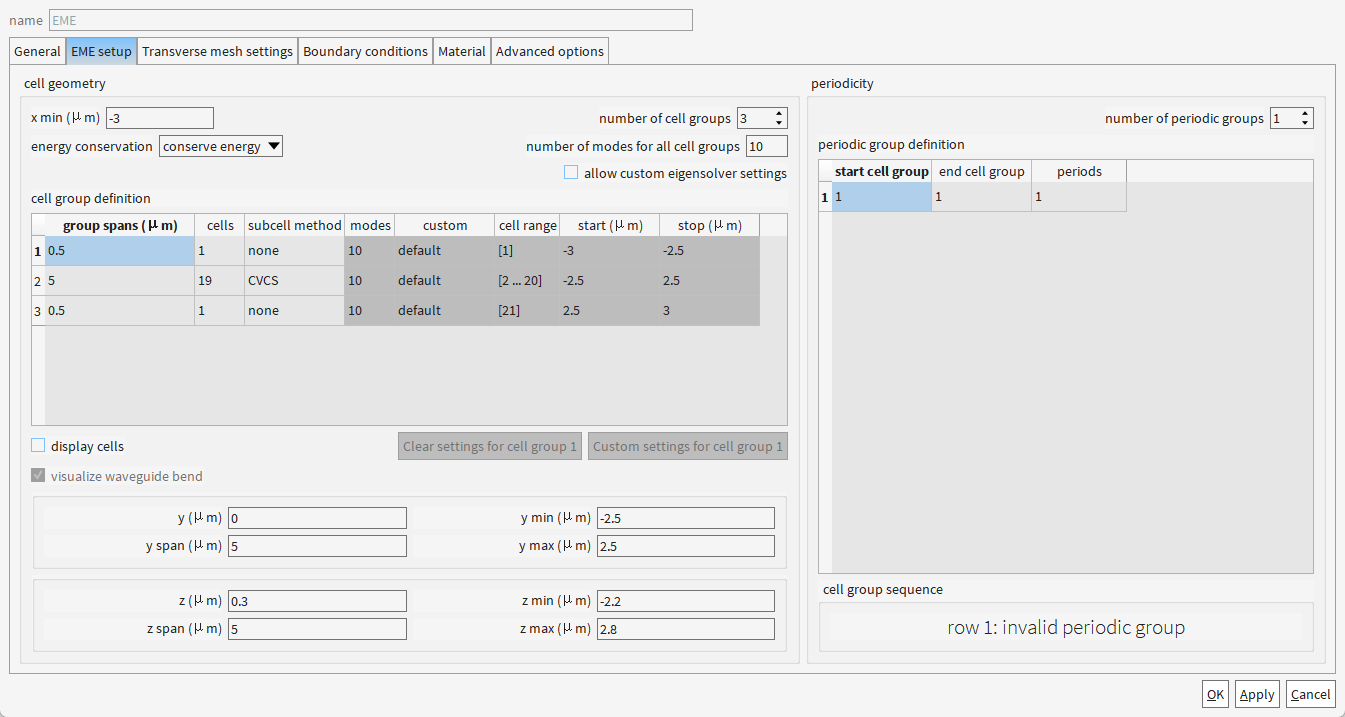
| 选项 | "none" (默认) | "CVCS" (恒定矢量电流片) | 当前设置 |
|---|---|---|---|
| 适用场景 | 结构简单、场变化平缓的区域(如均匀波导) | 复杂结构或高梯度场区域(如光栅、突变界面) | 第1、3组(0.5 μm均匀段)用none,第2组(5 μm密集光栅)用CVCS |
| 计算原理 | 直接全局求解亥姆霍兹方程,忽略子单元边界效应 | 将单元细分为子区域,用等效电流片修正边界场 | 第2组19个密集单元需高精度边界处理 |
| 计算速度 | ⚡️ 快(无额外细分) | ⏳ 慢(细分+边界计算) | 第2组计算时间可能增加3-5倍 |
| 精度 | 低(相位误差可能>1%) | 高(边界场误差<0.1%) | 确保光栅布拉格波长偏移<0.01 μm |
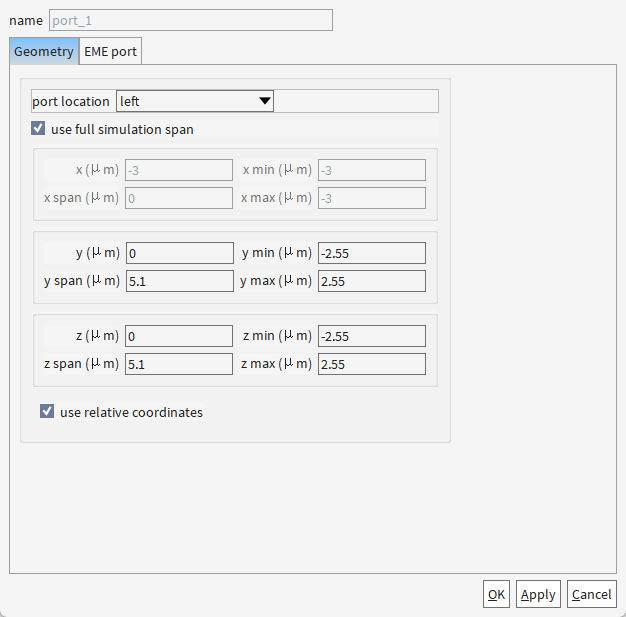
2.3 运行
完成后,使用 EME 分析窗口中的“Propagation sweep”小部件扫描从 5um 到 500um 的锥形长度(group span 2),然后单击“eme sweep”按钮。
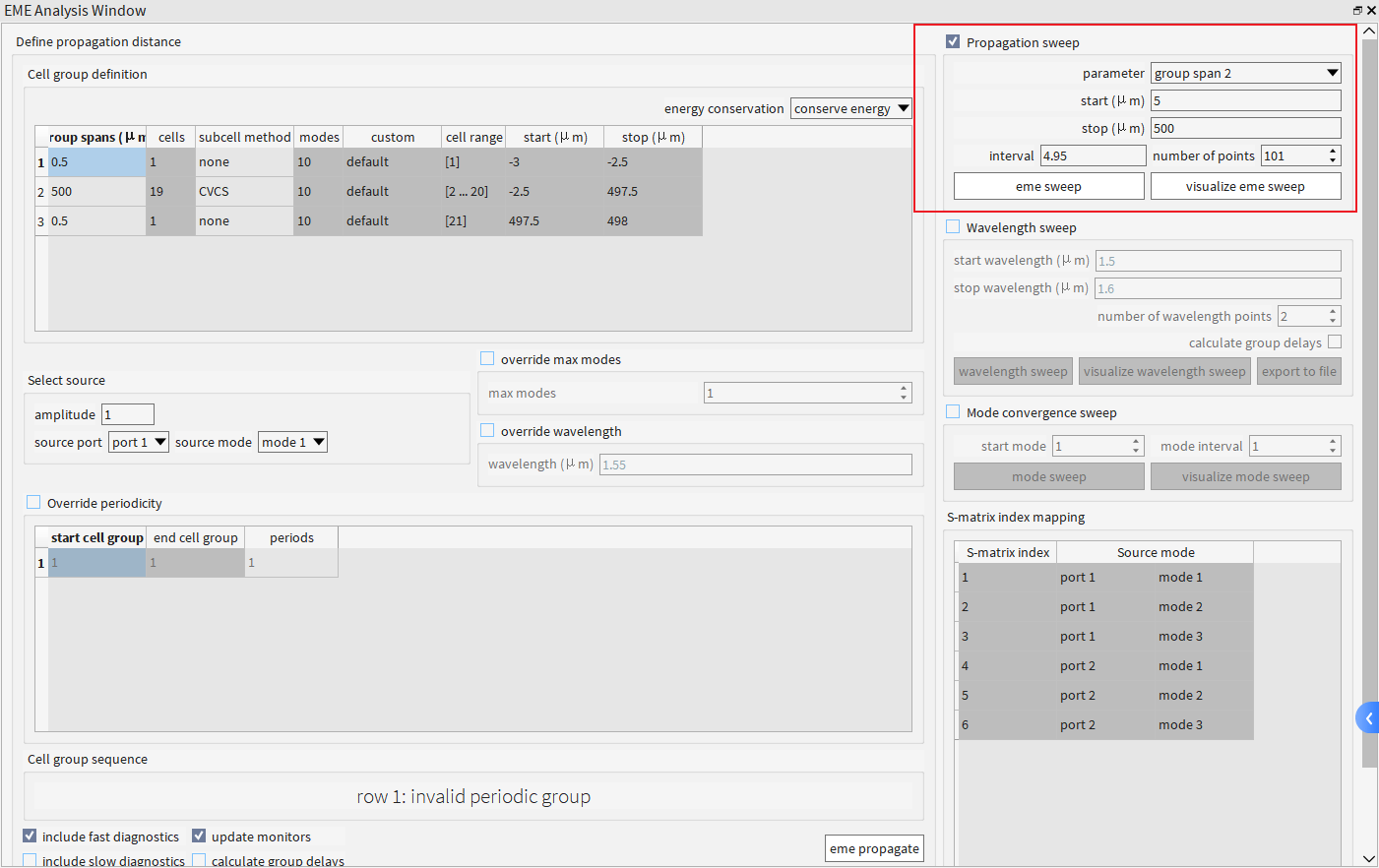
| 界面元素 | 参数名称 | 物理/数学意义 | 典型设置依据 | 当前值 |
|---|---|---|---|---|
| 复选框 | Propagation sweep | 启用传播扫描功能,对指定参数进行分段仿真 | 需分析器件性能随长度/位置的变化时启用 | √ 已勾选 |
| 下拉菜单 | parameter: group span 2 | 选择扫描变量为第2组单元的跨度(如光栅周期总长度) | 第2组通常对应核心功能区域(如光栅、耦合区) | group span 2 |
| 起始值 | start (μm) | 扫描的起始物理长度 | 根据器件最小有效长度设定(如光栅起始耦合长度) | 5 μm |
| 终止值 | stop (μm) | 扫描的终止物理长度 | 根据器件最大允许尺寸或饱和效应设定 | 500 μm |
| 步长/间隔 | interval | 相邻扫描点之间的长度增量 | 需满足奈奎斯特采样定理(至少2点/周期) | 4.95 μm |
| 点数 | number of points | 总扫描点数(= (stop-start)/interval + 1) | 平衡精度与计算量,通常≥10点/λ | 101 |
| 动作按钮 | eme sweep | 执行扫描计算,生成S参数矩阵等结果 | 需在设置完成后触发 | |
| 可视化按钮 | visualize eme sweep | 绘制扫描结果(如透射谱、模式能量分布) | 用于快速验证数据趋势 |
扫描出来的结果:
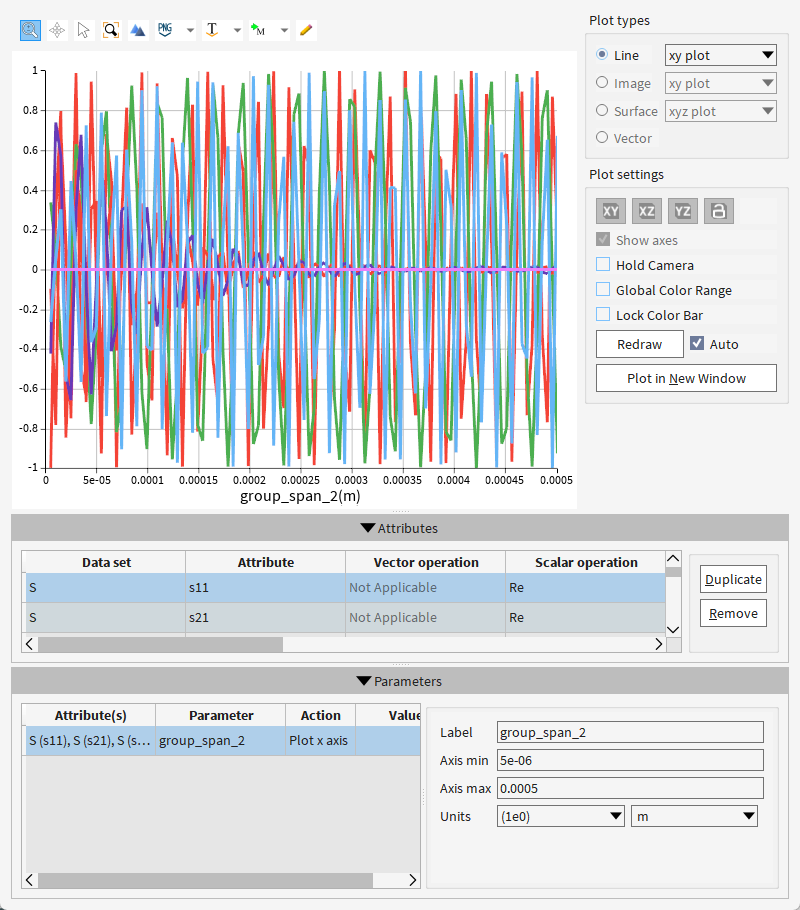
筛选后的结果:
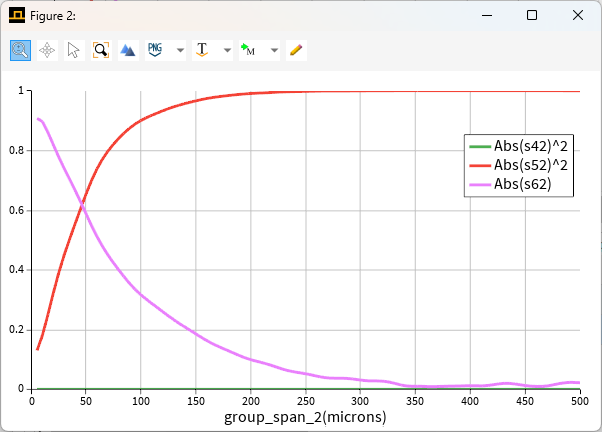
S矩阵索引映射表可以用来查看哪个S元素映射到哪个端口。 由于有 2 个端口(每个端口有 3 种模式),S42、S52、S62 将分别给出从 TE1 到 TE0、TE1 到 TM0 和 TE1 到 TE1 的转换效率。 可以单击“Remove”按钮来保留感兴趣的属性。 然后在“Scalar operation”下拉列表中选择“Abs^2”。 在下图中,可以看到没有能量从 TE1 转移到 TE0。 在 250um 左右的锥度长度处,TE1 模式几乎完全转移到 TM0 模式。
这个S矩阵是怎么看代表的是什么转换效率?
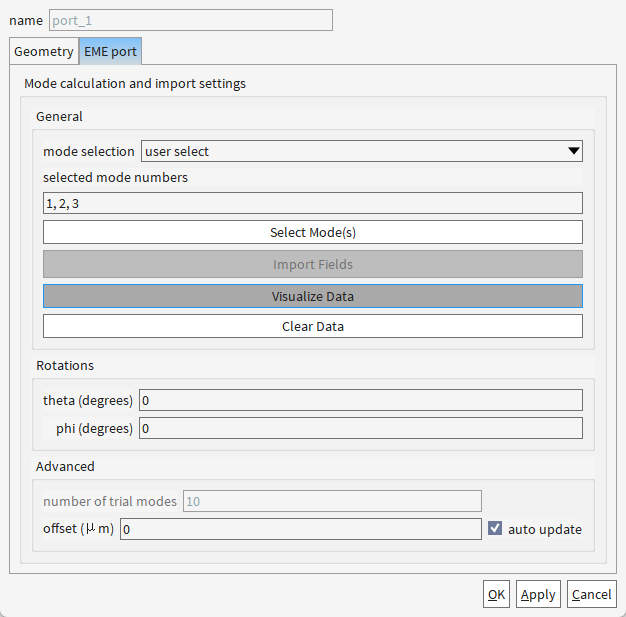
首先要注意当时user select模式1、2和3分别代表的是啥
port1:
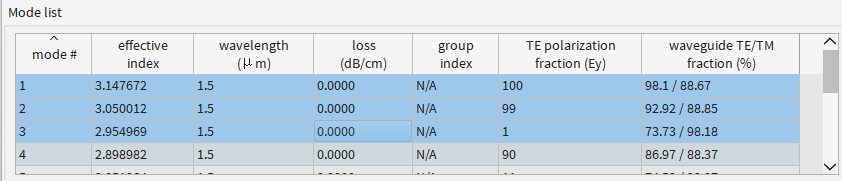
所以1、2、3分别代表TE0,TE1,TM0
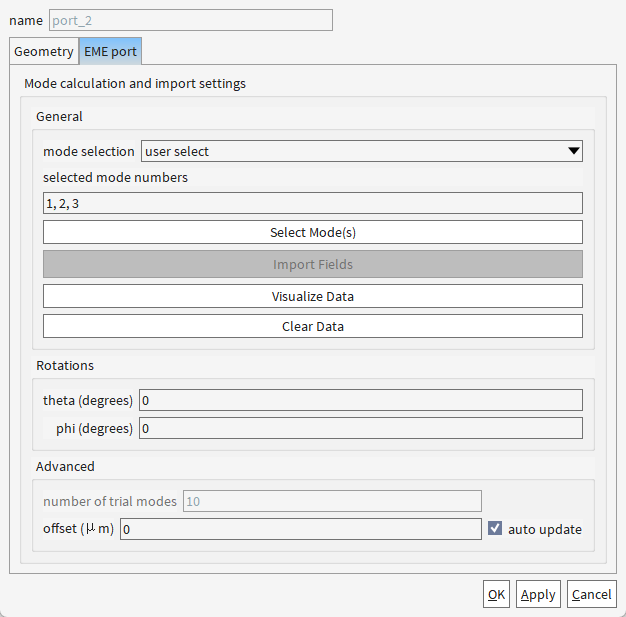
port2:
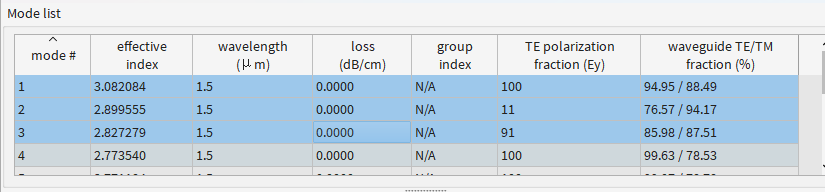
所以4、5、6分别代表TE0,TM0,TE1
举个例子来说,S42就是2-4,即从 TE1 到 TE0的转换效率。
