决策树模型知识点整理:从原理到实战(含可视化与调参)
从原理到实战:全面掌握决策树模型(含可视化与调参)
在机器学习入门阶段,有一种模型既直观又强大,那就是决策树(Decision Tree)。你可以把它想象成一次“二十问”游戏,通过一系列 yes/no 的问题,一步步将数据归类。本文将带你从理论原理、构建流程、模型调参,到可视化和与回归模型的对比,全面理解决策树,并最终掌握它在实际问题中的应用。
一、决策树是什么?
决策树是一种树状结构模型,它由节点和边组成:
- 根节点:第一个决策点。
- 决策节点:每个判断条件的地方。
- 叶节点:最终输出预测结果。
- 边:节点之间的连接,代表条件的满足或不满足。
你可以将它理解为“if…else…”语句的图形化表示,比如:
if 温度 > 25:if 是否下雨 == 否:预测 = 买冰激凌else:预测 = 不买
else:预测 = 不买
这就是最简单的一棵二叉分类树。
二、为什么选择决策树?
| 优势 | 描述 |
|---|---|
| 无需特征归一化 | 决策树对特征的量纲不敏感,节省预处理工作量。 |
| 对共线性不敏感 | 能自动选择最有效的特征,规避冗余。 |
| 可解释性强 | 每一步判断逻辑可视化后清晰直观。 |
| 同时支持分类与回归 | 分类任务用分类树,回归任务用回归树。 |
当然,决策树也有缺点,例如:容易过拟合、对少量样本波动敏感。这就需要通过剪枝或集成学习(如随机森林、XGBoost)来解决。
三、核心原理:基尼不纯度 & 最优分裂
什么是“纯度”?
在分类问题中,我们希望每个叶子节点越“纯”越好,也就是其中样本尽可能属于同一类别。
基尼不纯度的定义如下:
Gini(D) = 1 - ∑(p_k^2)
其中,p_k 是当前节点中第 k 类样本的比例。Gini 越低,说明节点越纯。
怎么选“最优特征 + 分裂点”?
- 遍历所有特征;
- 尝试每个特征的不同切分点;
- 计算分裂后两组子样本的加权平均 Gini;
- 选择 Gini 下降最多的组合作为最佳分裂。
四、建树流程详解
以下以 Python + Scikit-learn 为例:
1. 导入所需库
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import f1_score, confusion_matrix
import pandas as pd
2. 数据准备
假设我们预测客户是否流失,原始数据包含年龄、合同类型、通话时间等字段。
df = pd.read_csv("churn_data.csv")
X = df.drop("churn", axis=1)
y = df["churn"]# 类别变量编码
X = pd.get_dummies(X)# 划分训练/测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.3, random_state=42)
五、模型训练与可视化
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)
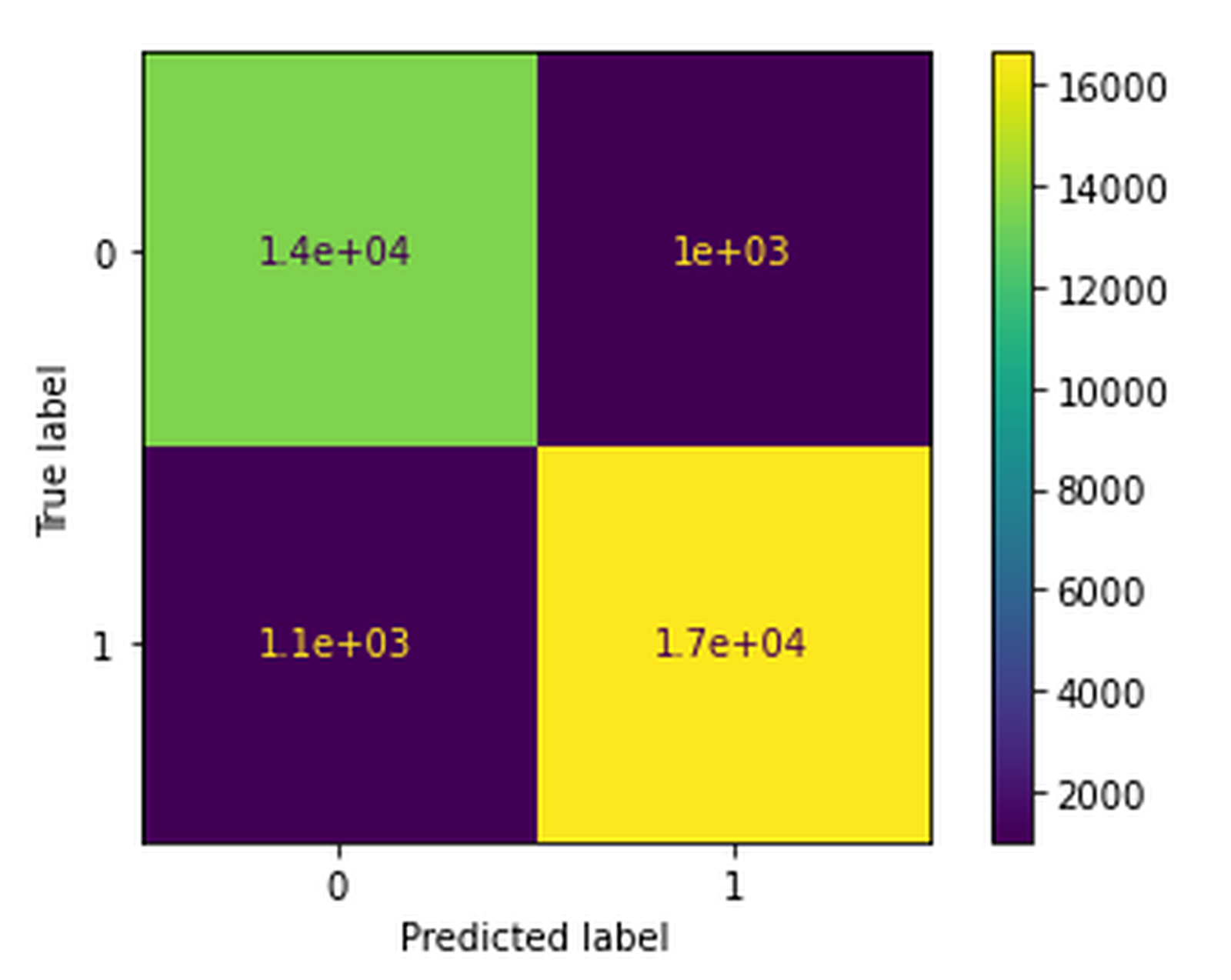
模型评估
y_pred = clf.predict(X_test)
f1 = f1_score(y_test, y_pred)
print("F1 Score:", f1)
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
可视化决策树
import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plot_tree(clf, feature_names=X.columns, class_names=["No", "Yes"], filled=True)
plt.show()
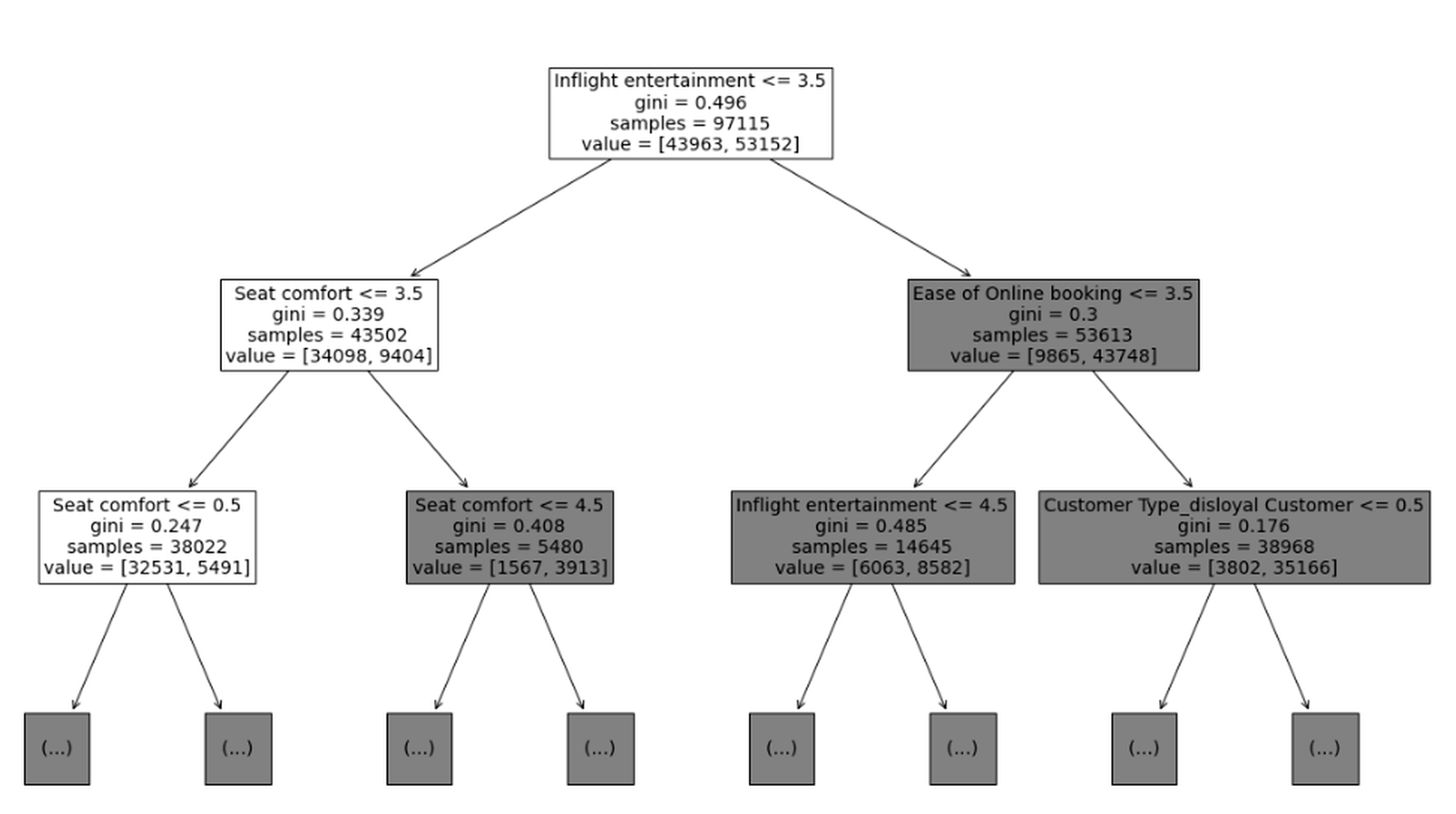
你可以从图中看到每个节点的特征、样本数量、Gini 值和最终分类。
六、超参数调优(防止过拟合)
决策树容易过拟合,解决办法是设置合适的“剪枝”超参数。
常见超参数解释:
max_depth: 最大深度,控制模型复杂度。min_samples_leaf: 每个叶子节点最少样本数,避免太“窄”的分支。criterion: 划分标准(如 ‘gini’ 或 ‘entropy’)。max_leaf_nodes: 限制叶节点总数,进一步压缩模型。
网格搜索调参
param_grid = {'max_depth': [3, 5, 10],'min_samples_leaf': [1, 5, 10]
}grid = GridSearchCV(DecisionTreeClassifier(random_state=42),param_grid=param_grid,scoring='f1',cv=5
)grid.fit(X_train, y_train)
print("Best params:", grid.best_params_)
七、决策树 vs 回归模型:谁更适合你?
| 维度 | 决策树 | 线性回归 |
|---|---|---|
| 模型类型 | 非参数 | 参数 |
| 特征关系 | 可处理非线性 | 只处理线性关系 |
| 可解释性 | 可视化为树结构 | 系数明确易解读 |
| 预处理需求 | 低 | 高(需归一化、哑变量) |
| 抗异常值能力 | 较强 | 敏感 |
| 容易过拟合 | 是 | 一般 |
举例:预测学生成绩
- 线性回归:建模“成绩 = 学习时长 × β₁ + 睡眠时间 × β₂”
- 决策树:学习时长 > 3小时 → 成绩高;否则 → 成绩低
八、模型验证:让你的模型更可靠
为了避免模型只记住训练数据,我们需要验证它在“没见过的数据”上的表现。
方法一:留出法
直接将原始数据分为训练集 + 测试集。
方法二:交叉验证(推荐)
from sklearn.model_selection import cross_val_score
scores = cross_val_score(clf, X, y, cv=5, scoring='f1')
print("CV F1 score:", scores.mean())
交叉验证对小样本尤为有用,因为它可以让所有数据都有机会成为测试集。
九、结语:掌握一棵“通人性”的树
决策树并不是最复杂的模型,但它有两个杀手级优势:
- 可解释性:每一步预测都能讲出原因,非常适合与业务部门沟通。
- 通用性:分类、回归、多任务建模都能胜任,还能作为集成方法的基底。
