算法思想之 多源 BFS 问题

欢迎拜访：雾里看山-CSDN博客
本篇主题：算法思想之 多源 BFS 问题
发布时间：2025.8.1
隶属专栏：算法

算法介绍

多源 BFS（Breadth-First Search）是单源 BFS 的扩展，核心思想是从多个起点同时开始扩散，利用 BFS “层次遍历” 的特性，高效求解 “多个源点到所有其他节点的最短距离” 问题。其优势在于避免了单源 BFS 的重复计算，时间复杂度更优。

多源 BFS 的核心原理

单源 BFS 从一个起点出发，按 “层次”（距离起点的距离）扩散，确保每个节点首次被访问时的距离是最短的。
多源 BFS 则将所有源点作为 “第 0 层”，同时放入队列，然后按层次依次扩散。此时，每个节点首次被访问时，对应的距离就是 “该节点到最近的源点的最短距离”。

这是因为 BFS 的层次遍历特性：先被访问的节点距离源点更近，而多源同时扩散时，节点首次被任何一个源点的扩散触及，就是其到最近源点的距离。

适用场景

多源 BFS 主要解决 “多源最短路径” 问题，典型场景包括：

• 网格中求每个单元格到最近 “0” 的距离（如 LeetCode 542. 01 矩阵）；
• 洪水扩散：多个起点同时向外蔓延，求每个点被淹没的最早时间；
• 图中多个起点到其他节点的最短距离（取最小值）。

与单源 BFS 的对比

以 “网格中求每个点到最近 0 的距离” 为例：

• 单源 BFS：需对每个 “0” 单独做一次 BFS，重复计算大量节点，时间复杂度为 O (k×m×n)（k 为 0 的数量，m、n 为网格尺寸），效率极低。
• 多源 BFS：一次性将所有 “0” 作为起点，一次遍历即可完成所有计算，时间复杂度为 O (m×n)，效率显著提升。

多源 BFS 的实现步骤

以 “网格问题” 为例（如二维网格，求每个点到最近源点的距离），步骤如下：

1. 确定源点：识别所有初始源点（如 “01 矩阵” 中的所有 0）。
2. 初始化数据结构：
   1. 队列：存储待扩散的节点（初始时放入所有源点）；
   2. 距离数组：记录每个节点到最近源点的距离（源点距离为 0，其他节点初始化为 - 1 或一个较大值，表示未访问）。
3. 层次遍历（BFS）：
   1. 每次从队列中取出当前层的所有节点（同一距离的节点）；
   2. 对每个节点的邻接节点（如网格中的上下左右）进行检查：若邻接节点未被访问（距离为 - 1），则更新其距离为 “当前节点距离 + 1”，并加入队列；
   3. 重复直至队列为空，此时距离数组即为结果。

关键细节与注意事项

距离数组初始化：源点距离必须设为 0，非源点初始为 -1（或其他标记），避免重复访问。

层次遍历的意义：BFS 的 “先进先出” 特性确保，节点首次被访问时的距离就是到最近源点的最短距离（无需考虑其他源点的更远路径）。

适用范围：不仅限于网格，也适用于一般图结构（如无向图、有向无权图），只需将图中所有源点初始入队即可。

例题

01 矩阵

题目链接

542. 01 矩阵

题目描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

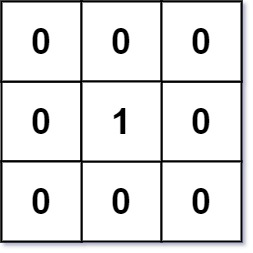
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

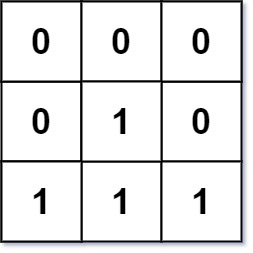
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：
m == mat.length

• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0

算法思路

我们可以先把所有的 0 都放在队列中，把它们当成一个整体，每次把当前队列里面的所有元素向外扩展一次。

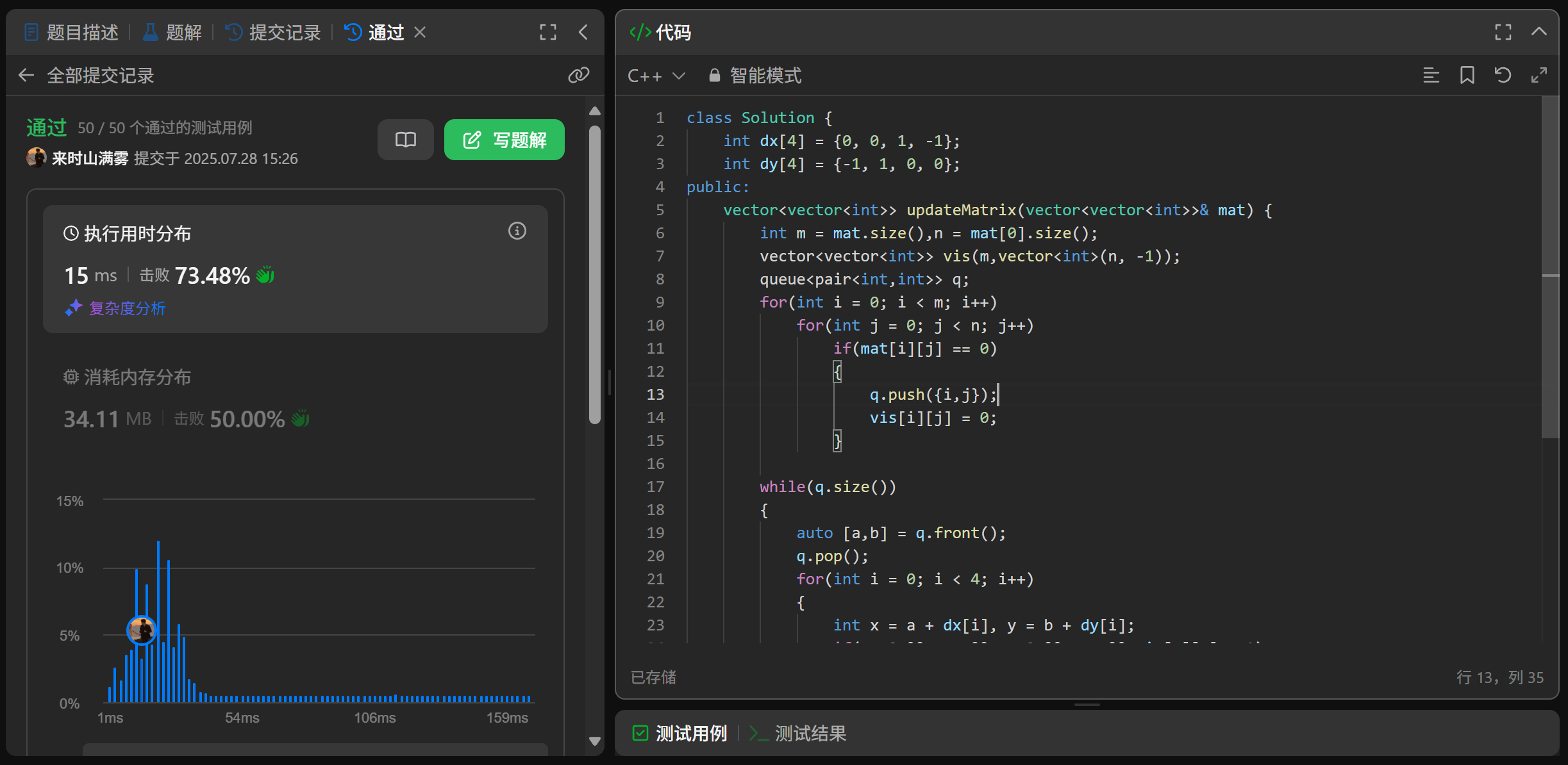
代码实现

class Solution {int dx[4] = {0, 0, 1, -1};int dy[4] = {-1, 1, 0, 0};
public:vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size(),n = mat[0].size();vector<vector<int>> vis(m,vector<int>(n, -1));queue<pair<int,int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(mat[i][j] == 0){q.push({i,j});vis[i][j] = 0;}while(q.size()){auto [a,b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b + dy[i];if(x>=0 && x<m && y>=0 && y<n && vis[x][y]==-1){vis[x][y] = vis[a][b]+1;q.push({x,y});}}}return vis;}
};

飞地的数量

题目链接

1020. 飞地的数量

题目描述

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

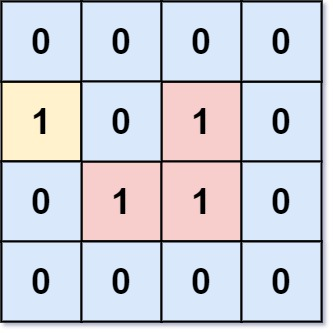
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

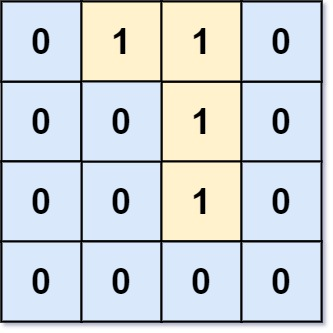
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 500
• grid[i][j] 的值为 0 或 1

算法思路

正难则反：

• 从边上的 1 开始搜索，把与边上 1 相连的联通区域全部标记一下；
• 然后再遍历一遍矩阵，看看哪些位置的 1 没有被标记即可

标记的时候，可以用 多源 bfs 解决。

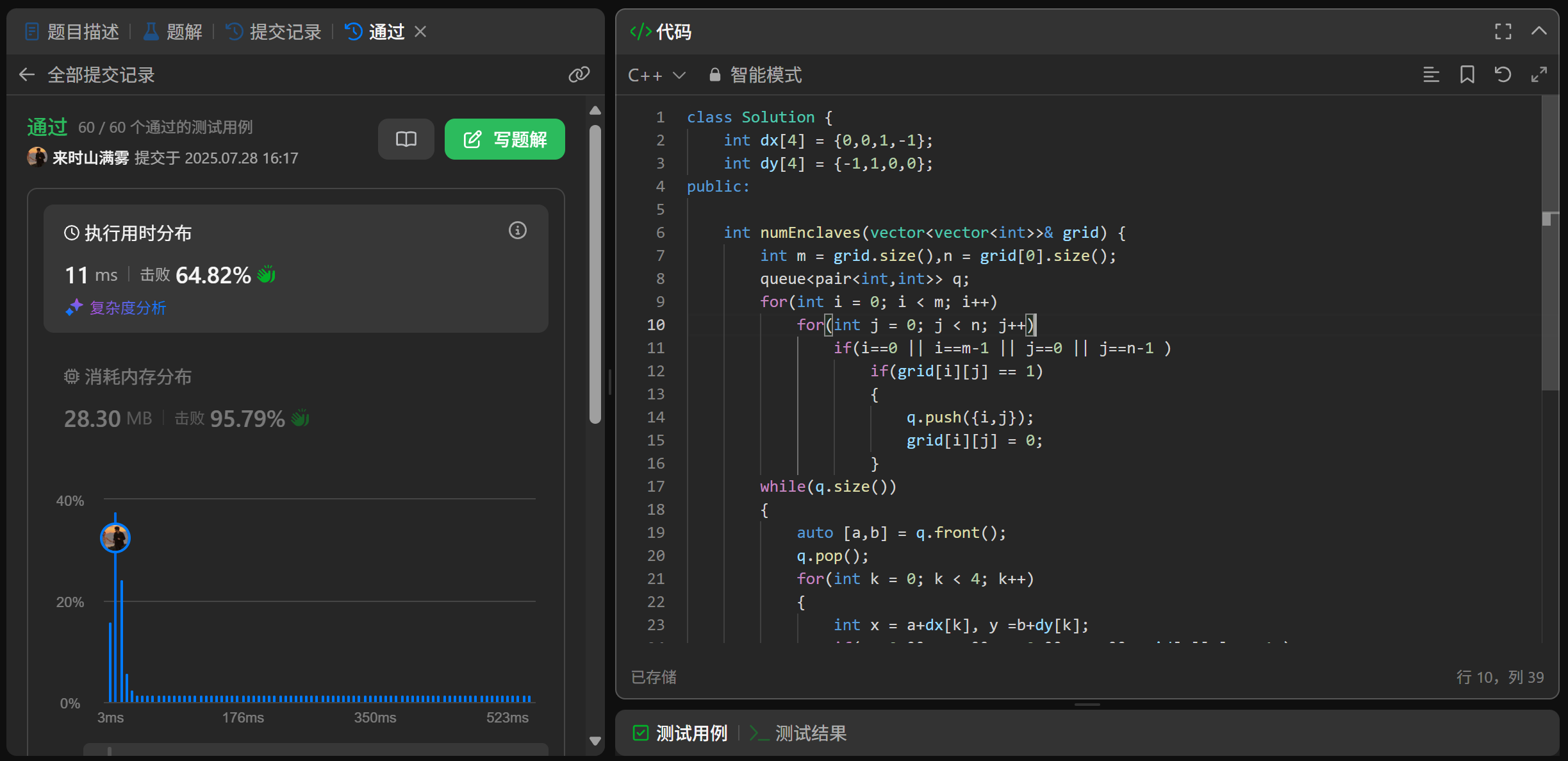
代码实现

class Solution {int dx[4] = {0,0,1,-1};int dy[4] = {-1,1,0,0};
public:int numEnclaves(vector<vector<int>>& grid) {int m = grid.size(),n = grid[0].size();queue<pair<int,int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(i==0 || i==m-1 || j==0 || j==n-1 )if(grid[i][j] == 1){q.push({i,j});grid[i][j] = 0;}while(q.size()){auto [a,b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a+dx[k], y =b+dy[k];if(x>=0 && x<m && y>=0 && y<n && grid[x][y] == 1 ){q.push({x,y});grid[x][y] = 0;} }}int ret = 0;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(grid[i][j] == 1)ret++;return ret;}};

地图中的最高点

题目链接

1765. 地图中的最高点

题目描述

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

• 如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
• 如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。

你需要按照如下规则给每个单元格安排高度：

• 每个格子的高度都必须是非负的。
• 如果一个格子是 水域 ，那么它的高度必须为 0 。
• 任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：

输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。

示例 2：

输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

提示：

• m == isWater.length
• n == isWater[i].length
• 1 <= m, n <= 1000
• isWater[i][j] 要么是 0 ，要么是 1 。
• 至少有 1 个水域格子。

算法思路

542. 01 矩阵的变型题，直接用多源 bfs 解决即可。

代码实现

class Solution {int dx[4] = {0,0,1,-1};int dy[4] = {-1,1,0,0};
public:vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {int m = isWater.size(),n = isWater[0].size();vector<vector<int>> ret(m, vector<int>(n,-1));queue<pair<int,int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(isWater[i][j] == 1){ret[i][j] = 0;q.push({i,j});}while(q.size()){auto [a,b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b+dy[i];if(x>=0 && x<m && y>=0 && y<n && ret[x][y]==-1){ret[x][y] = ret[a][b]+1;q.push({x,y});}}}return ret;}
};

地图分析

题目链接

1162. 地图分析

题目描述

你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是 曼哈顿距离（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释：
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释：
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] 不是 0 就是 1

算法思路

542. 01 矩阵的变型题，直接用多源 bfs 解决即可。

代码实现

class Solution {int dx[4] = {0,0,1,-1};int dy[4] = {-1,1,0,0};
public:int maxDistance(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> ret(m, vector<int>(n,-1));queue<pair<int,int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(grid[i][j] == 1){ret[i][j] = 0;q.push({i,j});}if(q.size() == m*n || q.size() == 0)return -1;int ans = 0;while(q.size()){auto [a,b] = q.front();q.pop();for(int i = 0; i < 4; i++){int x = a + dx[i], y = b+dy[i];if(x>=0 && x<m && y>=0 && y<n && grid[x][y]==0 && ret[x][y]==-1){ret[x][y] = ret[a][b]+1;ans = max(ans,ret[x][y]);q.push({x,y});}}}return ans;}
};

⚠️ 写在最后：以上内容是我在学习以后得一些总结和概括，如有错误或者需要补充的地方欢迎各位大佬评论或者私信我交流！！！