【Open3D】基础操作之三维变换

【Open3D】基础操作之三维变换

---

前言

Open3D 是一个开源库，旨在支持快速开发处理 3D 数据的软件。它提供了精心挑选的 C++ 和 Python 数据结构和算法，并且后端经过高度优化并设置为并行化。
官方文档：http://www.open3d.org/docs/
GitHub仓库：https://github.com/isl-org/Open3D

---

三维旋转

在三维空间中表示和计算旋转是计算机图形学、机器人学、航空航天等领域中的核心问题。主要有四种常用的方法：旋转矩阵 (Rotation Matrix)、旋转向量 (Rotation Vector)、欧拉角 (Euler Angles) 和 四元数 (Quaternions)。

o3d.geometry.TriangleMesh.create_coordinate_frame（创建表示坐标系的三角形网格的函数）

函数原型

o3d.geometry.TriangleMesh.create_coordinate_frame(size=1.0, origin=[0.0, 0.0, 0.0])

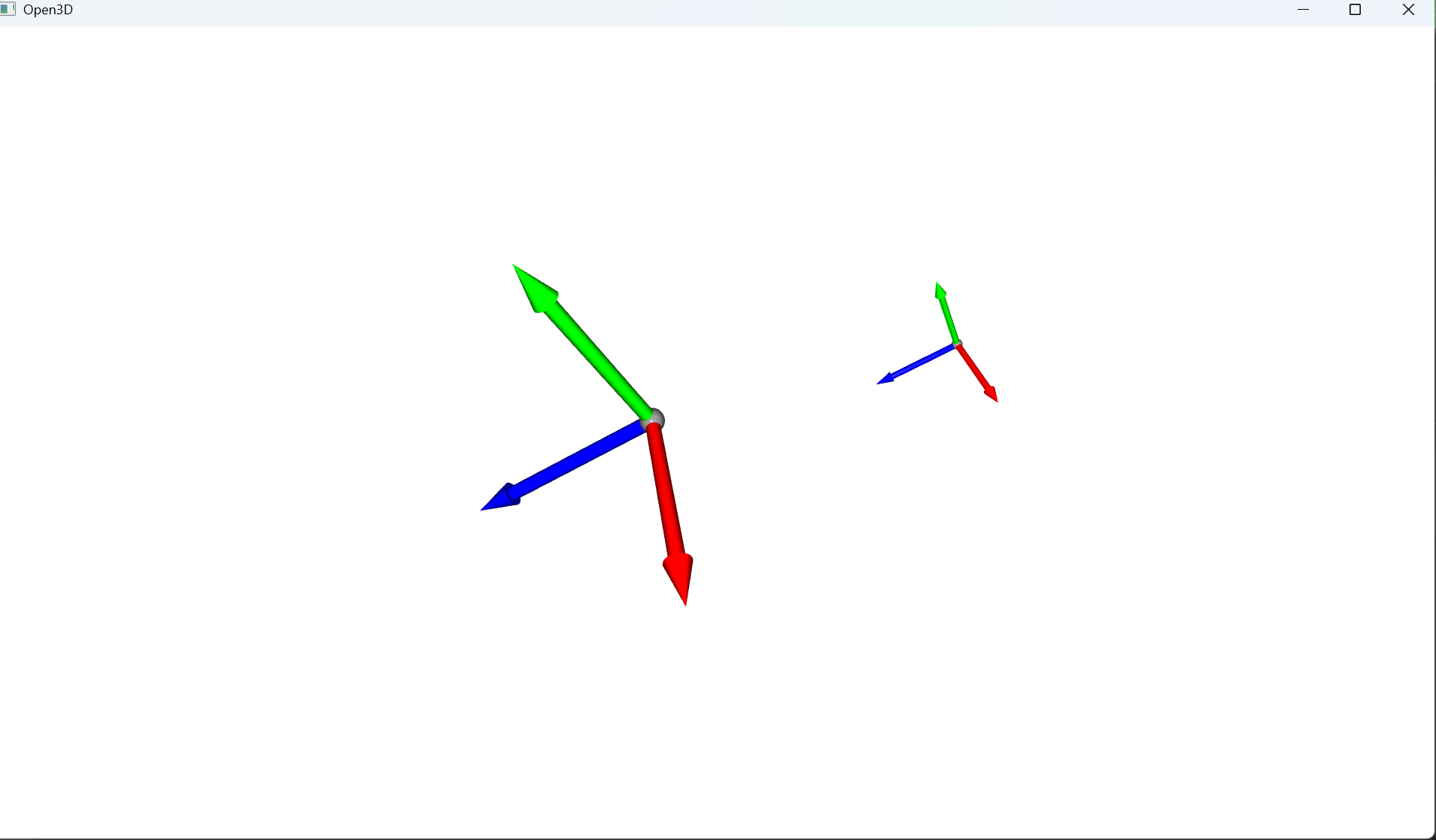
返回一个TriangleMesh对象，表示3D坐标系。

红色箭头表示 X 轴；绿色箭头表示 Y 轴；蓝色箭头表示 Z 轴。

参数	参数说明
size (float, 可选，默认值1.0)	坐标系的大小（比例因子），控制坐标轴的长度和整体大小。
origin (list[float], 可选，默认值[0.0, 0.0, 0.0])	坐标系原点的位置，格式为 [x, y, z]。

示例

import open3d as o3d# 创建默认大小的坐标系（原点在[0,0,0]，大小为1.0）
coord_frame = o3d.geometry.TriangleMesh.create_coordinate_frame()
# 创建自定义坐标系（原点在[1,2,3]，大小为2.0）
custom_coord_frame = o3d.geometry.TriangleMesh.create_coordinate_frame(size=2.0, origin=[1.0, 2.0, 3.0]
)
# 可视化
o3d.visualization.draw_geometries([coord_frame, custom_coord_frame])

Rotation Matrix（旋转矩阵）

旋转矩阵是一个3x3的矩阵，用来描述一个刚体绕着某个固定点（通常是原点）进行旋转的情况。用3x3 旋转矩阵 $\mathbf{R}$来旋转一个三维空间中的点或向量 $\mathbf{v}=[x,y,z{]}^T$ ：
$${\mathbf{v}}^{\prime }=\mathbf{Rv}=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\mathbf{v}$$

后续的旋转向量、欧拉角和 四元数最终都需要先转化成旋转矩阵，然后再进行旋转变换。

o3d.geometry.rotate（对几何对象进行旋转变换的函数）

适用于 TriangleMesh、PointCloud、LineSet 等几何类型。
函数原型

geometry.rotate(R, center=(0, 0, 0))

没有显式返回值，直接修改调用它的几何对象的顶点坐标。

参数	参数说明
R (np.ndarray)	3x3 的旋转矩阵。
center (tuple/list, 可选，默认为原点(0, 0, 0))	旋转中心的坐标，格式为 (x, y, z)。

Rotation Vector（旋转向量）

旋转向量使用一个三维向量来同时描述旋转轴和旋转角度，旋转向量的方向表示旋转轴的方向，而其长度（或者说模）则代表旋转的角度大小。给定一个旋转向量$\mathbf{r}=(r_x,r_y,r_z)$ ，其对应的旋转轴为单位向量$\mathbf{n}=(n_x,n_y,n_z)$，旋转角度为$\theta$，则有$\mathbf{r}=\theta \mathbf{n}$。

公式 $r=\theta n$ 中的乘法把旋转角度 $\theta$ 这个数值直接乘以表示旋转轴方向的单位向量 $n$，得到的向量 $r$ 同时包含了旋转轴的方向（由其方向决定）和旋转角度的大小（由其长度决定）。

要将一个三维点$\mathbf{p}=(x,y,z)$绕此旋转轴旋转指定角度，可以使用罗德里格斯公式得到旋转后的点${\mathbf{p}}^{\prime }$：
$${\mathbf{p}}^{\prime }=\cos \theta \mathbf{p}+(1-\cos \theta )(\mathbf{p}\cdot \mathbf{n})\mathbf{n}+\sin \theta (\mathbf{n}\times \mathbf{p})$$
另一种常见的方法是使用旋转矩阵，对于绕任意轴 $n$ 旋转角度 $\theta$ 的情况，旋转矩阵 $R$ 可以根据旋转向量计算得到：
$$R=\left[\begin{array}{ccc}\cos \theta +n_x^2(1-\cos \theta )& n_x{n}_y(1-\cos \theta )-n_z\sin \theta & n_x{n}_z(1-\cos \theta )+n_y\sin \theta \\ n_y{n}_x(1-\cos \theta )+n_z\sin \theta & \cos \theta +n_y^2(1-\cos \theta )& n_y{n}_z(1-\cos \theta )-n_x\sin \theta \\ n_z{n}_x(1-\cos \theta )-n_y\sin \theta & n_z{n}_y(1-\cos \theta )+n_x\sin \theta & \cos \theta +n_z^2(1-\cos \theta )\end{array}\right]$$

o3d.geometry.get_rotation_matrix_from_axis_angle（从旋转向量生成旋转矩阵的函数）

o3d.geometry.get_rotation_matrix_from_axis_angle(axis_angle)

返回一个 3x3 的旋转矩阵 。

参数	参数说明
axis_angle (np.ndarray)	形状为(3,)的数组，旋转轴的方向向量，包含三个欧拉角，顺序为绕X、Y、Z轴的旋转角度。

示例：

import open3d as o3d
import numpy as np
import copy# 创建原始坐标系
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()  # 深拷贝坐标系用于旋转
mesh_r = copy.deepcopy(mesh)    # 定义旋转向量（注意：这里的向量不是分别绕XYZ轴旋转，而是沿某个轴的旋转）
# np.pi/2 是 90度, np.pi/3 是 60度, np.pi/4 是 45度
rotation_vector = np.array([np.pi / 2, np.pi / 3, np.pi / 4])# 将旋转向量转换为旋转矩阵
# 输入表示的是旋转轴方向和旋转角度的组合,不是欧拉角
R = o3d.geometry.get_rotation_matrix_from_axis_angle(rotation_vector)   print("总的旋转矩阵:")
print(R)# 应用旋转,以原点为中心
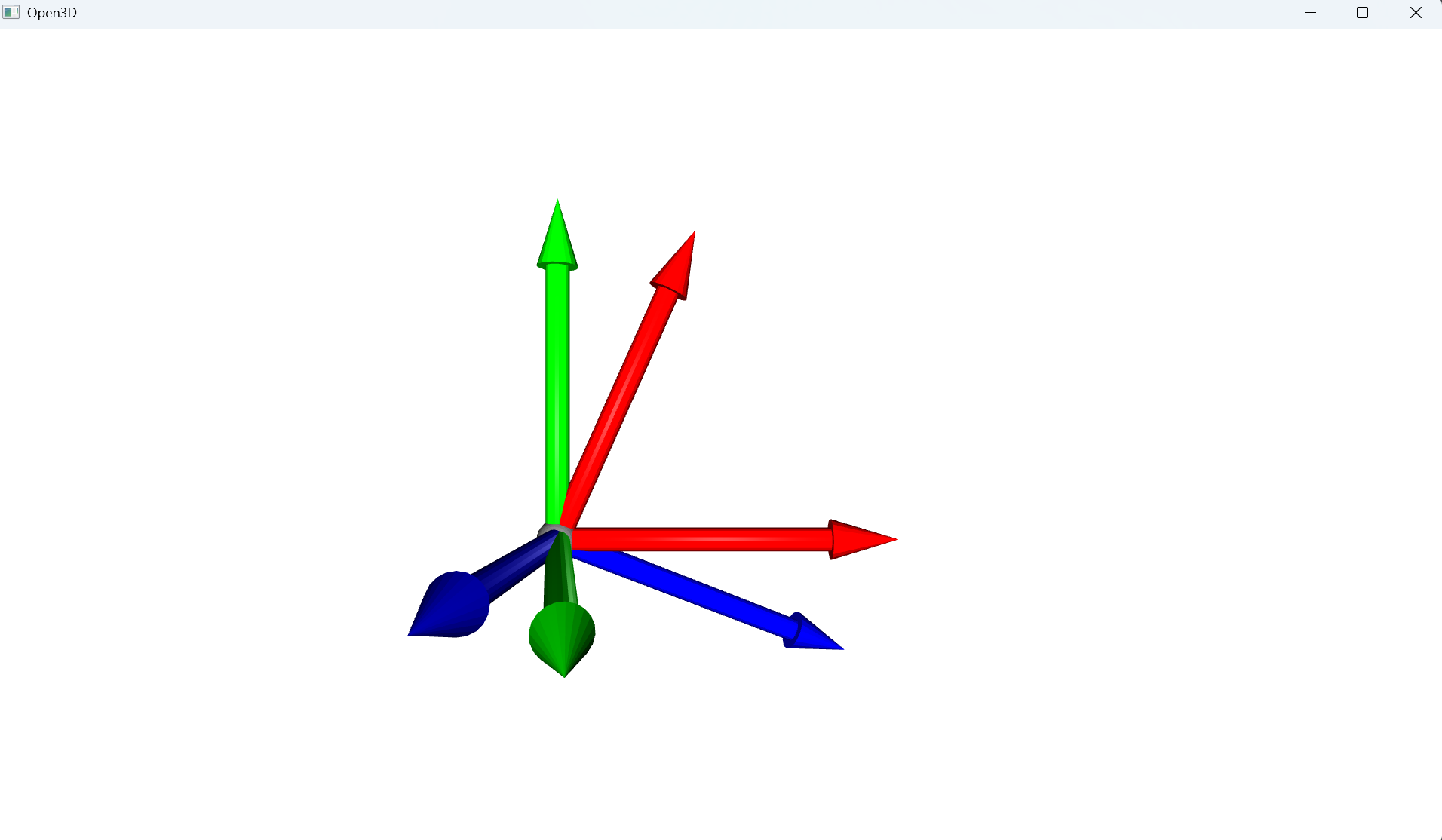
mesh_r.rotate(R, center=(0, 0, 0))  # 可视化原始和旋转后的坐标系
o3d.visualization.draw_geometries([mesh, mesh_r])

Euler Angles（欧拉角）

欧拉角通过三个角度来表示一个刚体在三维空间中的旋转状态，这三个角度通常代表了绕着特定坐标轴的三次连续旋转。根据选择的旋转顺序不同，可以有多种不同的欧拉角定义方式。

常见的旋转顺序包括XYZ、XZY、YXZ、YZX、ZXY和ZYX等，这些旋转顺序分别代表了按照选定的顺序依次绕着坐标系的X轴、Y轴和Z轴进行旋转。

以下是绕三个基本坐标轴旋转的旋转矩阵。

• 绕$X$轴旋转$\alpha$角的旋转矩阵：
  $$R_x(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& \cos \alpha & -\sin \alpha \\ 0& \sin \alpha & \cos \alpha \end{array}\right]$$
• 绕$Y$轴旋转$\beta$角的旋转矩阵：
  $$R_y(\beta )=\left[\begin{array}{ccc}\cos \beta & 0& \sin \beta \\ 0& 1& 0\\ -\sin \beta & 0& \cos \beta \end{array}\right]$$
• 绕$Z$轴旋转$\gamma$角的旋转矩阵：
  $$R_z(\gamma )=\left[\begin{array}{ccc}\cos \gamma & -\sin \gamma & 0\\ \sin \gamma & \cos \gamma & 0\\ 0& 0& 1\end{array}\right]$$

总的旋转矩阵可以通过将这三个单独的旋转矩阵相乘得到，对于ZYX顺序的欧拉角变换，其对应的旋转矩阵为：
$$R=R_z(\gamma )\cdot R_y(\beta )\cdot R_x(\alpha )=\left[\begin{array}{ccc}\cos \gamma \cos \beta & \cos \gamma \sin \beta \sin \alpha -\sin \gamma \cos \alpha & \cos \gamma \sin \beta \cos \alpha +\sin \gamma \sin \alpha \\ \sin \gamma \cos \beta & \sin \gamma \sin \beta \sin \alpha +\cos \gamma \cos \alpha & \sin \gamma \sin \beta \cos \alpha -\cos \gamma \sin \alpha \\ -\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha \end{array}\right]$$

o3d.geometry.get_rotation_matrix_from_AAA（从欧拉角生成旋转矩阵的函数）

函数原型

o3d.geometry.get_rotation_matrix_from_AAA(rotation)

AAA具体表示的函数	旋转顺序	说明
get_rotation_matrix_from_xyz	X→Y→Z	先绕X轴，再绕Y轴，最后绕Z轴
get_rotation_matrix_from_xzy	X→Z→Y	先绕X轴，再绕Z轴，最后绕Y轴
get_rotation_matrix_from_yxz	Y→X→Z	先绕Y轴，再绕X轴，最后绕Z轴
get_rotation_matrix_from_yzx	Y→Z→X	先绕Y轴，再绕Z轴，最后绕X轴
get_rotation_matrix_from_zxy	Z→X→Y	先绕Z轴，再绕X轴，最后绕Y轴
get_rotation_matrix_from_zyx	Z→Y→X	先绕Z轴，再绕Y轴，最后绕X轴
get_rotation_matrix_from_xyx	X→Y→X	两次绕X轴（经典欧拉角
get_rotation_matrix_from_xzx	X→Z→X	两次绕X轴（经典欧拉角
get_rotation_matrix_from_yxy	Y→X→Y	两次绕Y轴（经典欧拉角
get_rotation_matrix_from_yzy	Y→Z→Y	两次绕Y轴（经典欧拉角
get_rotation_matrix_from_zxz	Z→X→Z	两次绕Z轴（经典欧拉角
get_rotation_matrix_from_zyz	Z→Y→Z	两次绕Z轴（经典欧拉角

返回一个 3x3 的旋转矩阵 。

参数	参数说明
rotation (np.ndarray)	显式格式：形状为(4,)的数组，前三个元素是旋转轴向量(x, y, z)，第四个元素是旋转角度（弧度）； 紧凑格式：形状为(3,)的数组，旋转向量的方向表示旋转轴，旋转向量的模长表示旋转角度（弧度）。

示例：

import open3d as o3d
import numpy as np
import copy# 创建原始坐标系
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()# 深拷贝坐标系用于旋转
mesh_r = copy.deepcopy(mesh)# 定义欧拉角（绕X轴旋转90度，绕Y轴旋转60度，绕Z轴旋转45度）
# 弧度
euler_angles = np.array([np.pi / 2,  # X轴: 90度 (π/2)np.pi / 3,  # Y轴: 60度 (π/3)np.pi / 4])  # Z轴: 45度 (π/4)# 将欧拉角转换为旋转矩阵 (使用 ZYX 旋转顺序)
R = o3d.geometry.get_rotation_matrix_from_zyx(euler_angles)   print("总的旋转矩阵 (XYZ顺序):")
print(R)# 应用旋转,以原点为中心
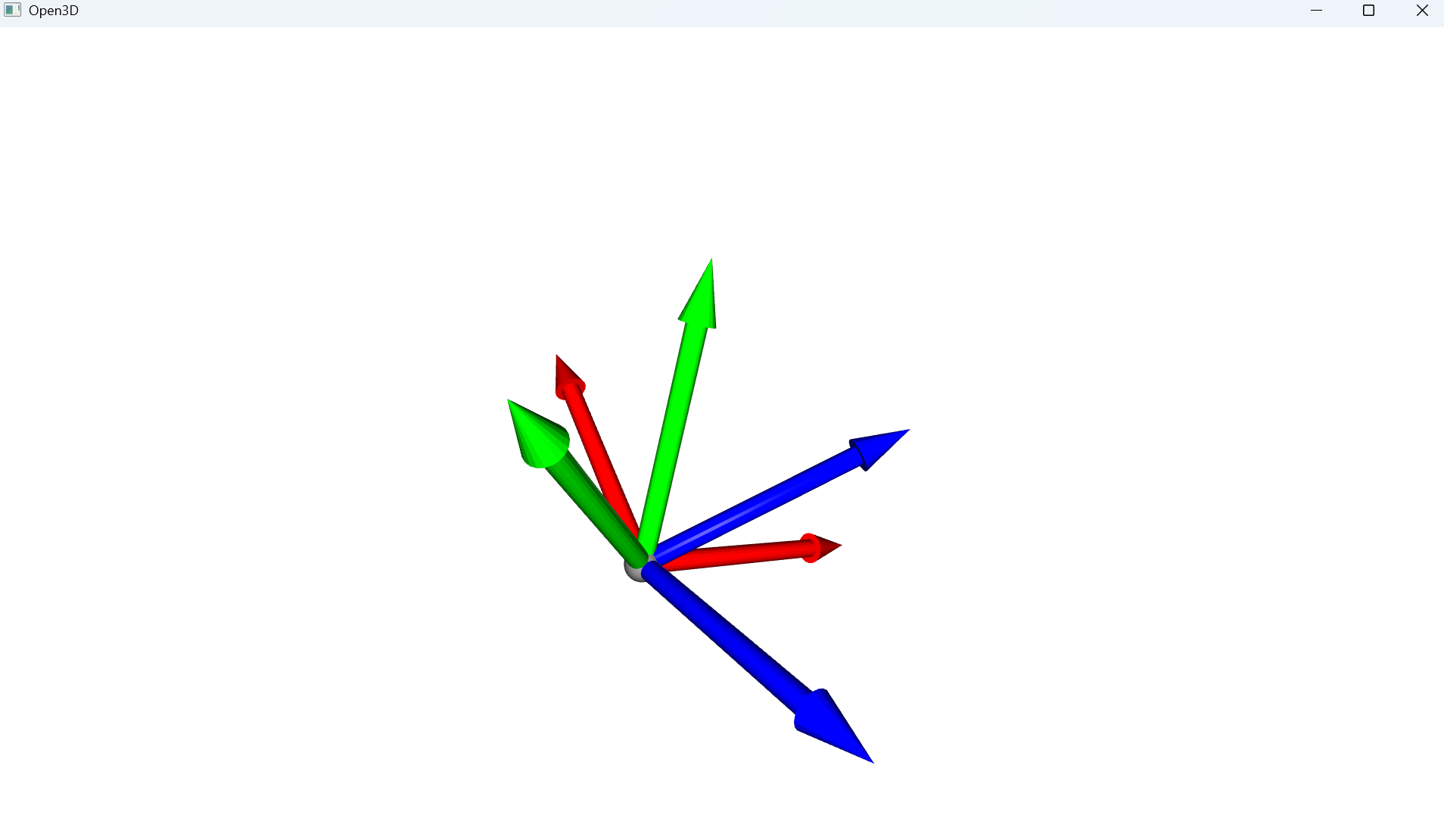
mesh_r.rotate(R, center=(0, 0, 0))# 可视化原始和旋转后的坐标系
o3d.visualization.draw_geometries([mesh, mesh_r])

Quaternions（四元数）

四元数是一个扩展了复数概念的数学实体，由一个实部和三个虚部组成，可以用来表示三维空间中的旋转。
四元数 $q=[w,x,y,z]$形式上可以写作：
$$q=w+xi+yj+zk$$
对应的旋转矩阵 $R$ 表示为：
$$R=\left[\begin{array}{ccc}1-2(y^2+z^2)& 2(xy-wz)& 2(xz+wy)\\ 2(xy+wz)& 1-2(x^2+z^2)& 2(yz-wx)\\ 2(xz-wy)& 2(yz+wx)& 1-2(x^2+y^2)\end{array}\right]$$

这里需要注意的是，四元数 $q$ 应该是单位四元数（即满足 $w^2+x^2+y^2+z^2=1$），这样才能正确表示一个旋转。如果不是单位四元数，则需要先将其归一化

o3d.geometry.get_rotation_matrix_from_quaternion（从四元素生成旋转矩阵的函数）

函数原型

o3d.geometry.get_rotation_matrix_from_quaternion(quaternion)

返回一个 3x3 的旋转矩阵 。

参数	参数说明
quaternion (np.ndarray)	旋转的四元数，顺序为 (w, x, y, z)。

示例：

import open3d as o3d
import numpy as np
import copy# 创建原始坐标系
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()# 深拷贝坐标系用于旋转
mesh_r = copy.deepcopy(mesh)# 定义一个四元数[w,x,y,z]
quat = np.array([0.7330127, 0.30940108, 0.58508386, 0.15891862])
# 从四元数获取旋转矩阵
R = o3d.geometry.get_rotation_matrix_from_quaternion(quat)print("旋转矩阵:")
print(R)# 应用旋转,以原点为中心
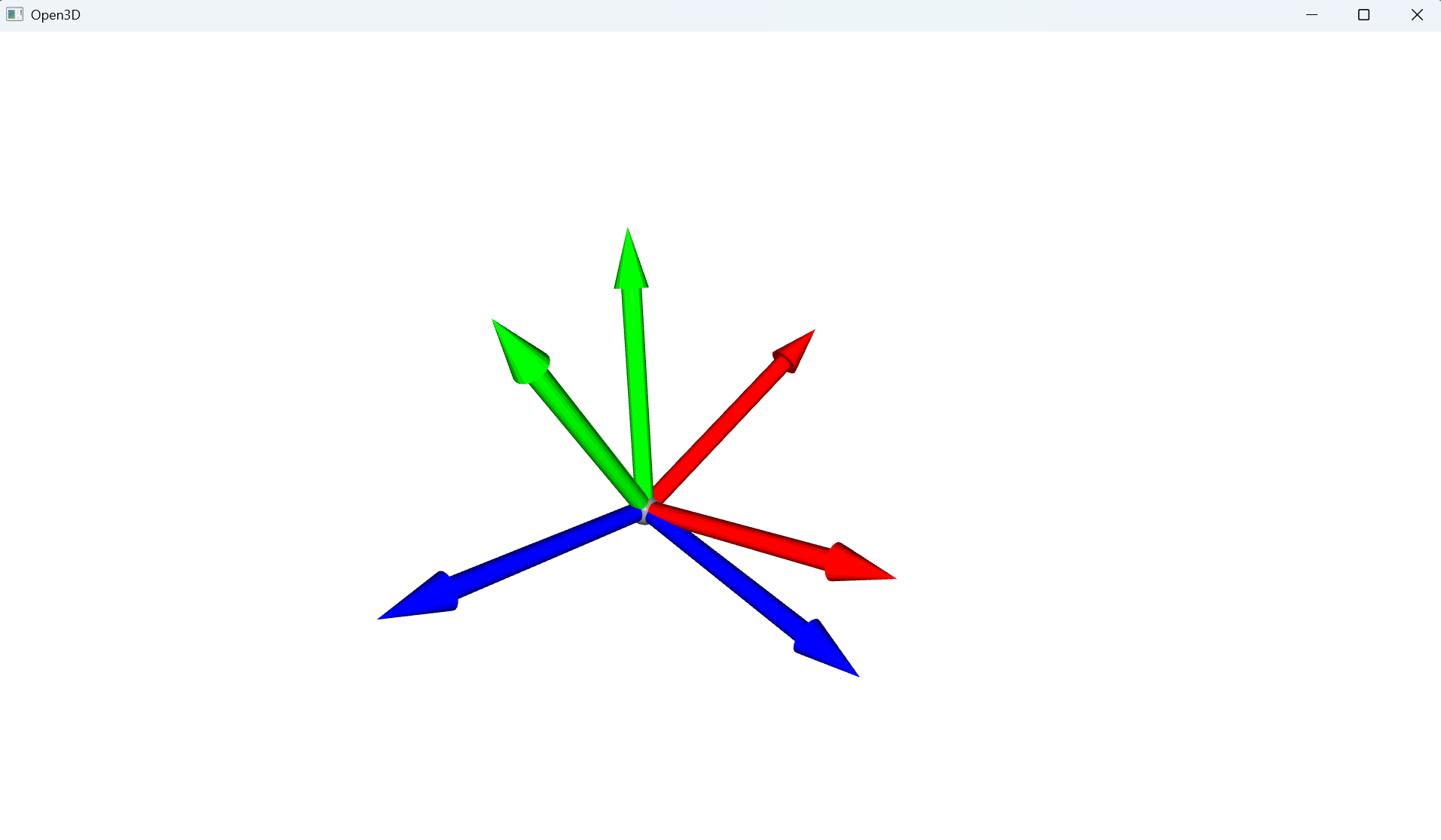
mesh_r.rotate(R, center=(0, 0, 0))# 可视化原始和旋转后的坐标系
o3d.visualization.draw_geometries([mesh, mesh_r])

---

三维平移和缩放

Translation（平移）

在三维空间中，平移变换是最基本的几何变换之一，用于将点或物体沿指定方向移动固定距离，只是它在空间中的位置发生了变化。
原始点坐标: $P=(x,y,z)$，平移$T=(t_x,t_y,t_z)$后的新坐标:
$$P^{\prime }=P+T=\left(\begin{array}{c}x+t_x\\ y+t_y\\ z+t_z\end{array}\right)$$
其中，$t_x$, $t_y$, 和 $t_z$ 分别表示在 $x$ 轴、$y$ 轴和 $z$ 轴方向上的平移距离。

o3d.geometry.translate（对几何对象进行平移操作的函数）

适用于 TriangleMesh、PointCloud、LineSet 等几何类型。
函数原型

geometry.translate(T, relative=True)

没有显式返回值，直接修改调用它的几何对象的顶点坐标。

参数	参数说明
T (np.ndarray,list)	形状需为[3,]，平移向量的三维数组 [tx, ty, tz]。
relative (bool, 可选，默认为True)	True相对平移，在当前基础上增加平移量；False绝对平移，将物体中心移动到指定位置。

示例：

import open3d as o3d
import copy# 创建原始坐标系
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame()# 深拷贝坐标系用于旋转
mesh_t = copy.deepcopy(mesh)# 设置平移向量 (X, Y, Z 三个方向的平移距离)
T = (2, 2, 2)# 平移操作（绝对平移）
mesh_t.translate(T, relative=False)# 可视化原始和旋转后的坐标系
o3d.visualization.draw_geometries([mesh, mesh_t])

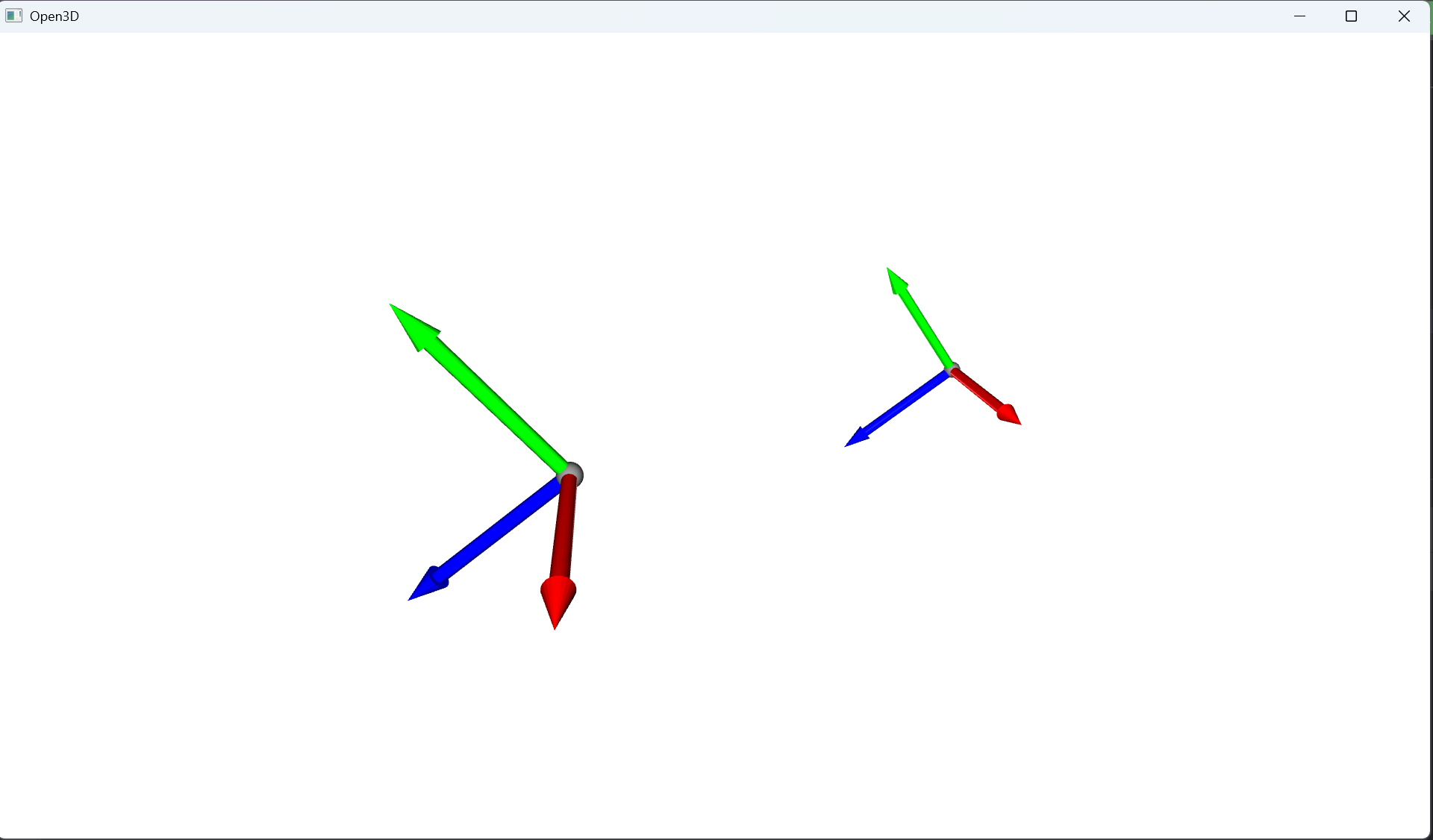
Scale（缩放）

在三维空间中，缩放变换是另一种基本的几何变换，用于改变点或物体的大小。通过缩放变换，我们可以使物体变大或变小，而其形状保持不变。
原始点坐标: $P=(x,y,z)$，缩放因子 $S=(s_x,s_y,s_z)$ 后的新坐标:
$$P^{\prime }=P\cdot S=\left(\begin{array}{c}x\cdot s_x\\ y\cdot s_y\\ z\cdot s_z\end{array}\right)$$
其中，$s_x$, $s_y$, 和 $s_z$ 分别表示在 $x$ 轴、$y$ 轴和 $z$ 轴方向上的缩放比例。如果 $s_x=s_y=s_z$，则物体将均匀缩放；否则，物体将进行非均匀缩放，导致物体在不同轴方向上的尺寸变化不一致。

o3d.geometry.translate（对几何对象进行缩放操作的函数）

适用于 TriangleMesh、PointCloud、LineSet 等几何类型。
函数原型

geometry.scale(S, center=None)

没有显式返回值，直接修改调用它的几何对象的顶点坐标。

参数	参数说明
S (float)	所有轴按相同比例缩放。
center (np.ndarray或list)	缩放中心点坐标。

示例：

import open3d as o3d
import copy# 创建原始坐标系
mesh = o3d.geometry.TriangleMesh.create_coordinate_frame(size=1.0)  # 设置初始大小# 深拷贝坐标系用于缩放
mesh_s = copy.deepcopy(mesh)# 设置缩放因子 (X, Y, Z 三个方向的缩放比例)
scale_factor = 2.0  # 均匀放大2倍# 执行缩放操作（相对于物体自身坐标系原点）
mesh_s.scale(scale_factor, center=mesh_s.get_center())# 可视化原始和缩放后的坐标系
o3d.visualization.draw_geometries([mesh, mesh_s])

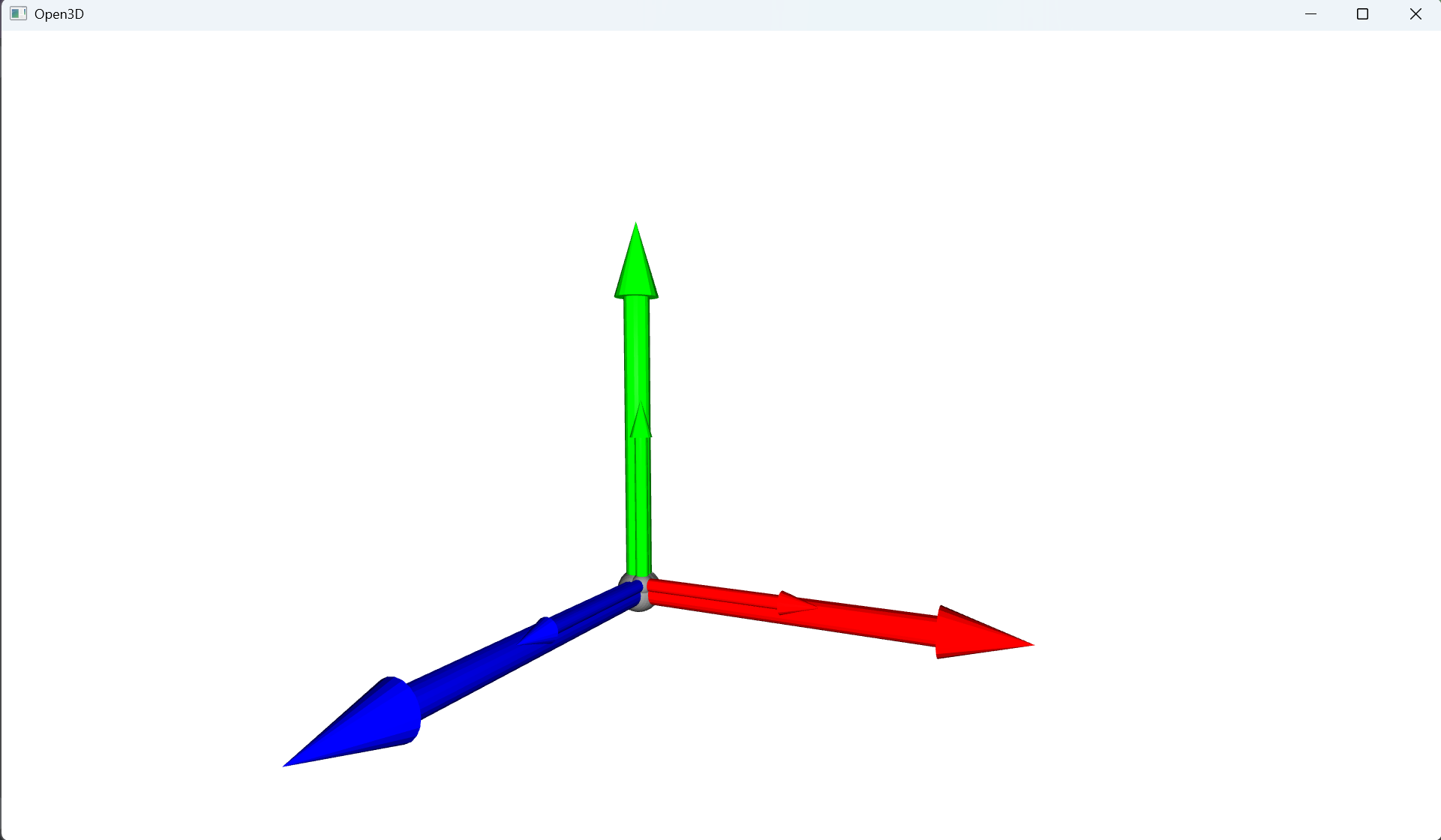
o3d.geometry.get_center（计算并返回几何体的中心点的函数）

适用于 TriangleMesh、PointCloud、LineSet 等几何类型。
函数原型

geometry.get_center()

返回一个中心点坐标的 np.ndarray数组 [cx, cy, cz]。

---

总结

Open3D的三维变换基本操作。