循环神经网络RNN原理精讲,详细举例!
第一部分:为什么需要RNN?
在了解RNN是什么之前,我们先要明白它解决了什么问题。
传统的神经网络,比如我们常见的前馈神经网络(Feedforward Neural Network)或者卷积神经网络(CNN),它们有一个共同的特点:输入之间是相互独立的。
你给它一张猫的图片,它判断是猫。再给它一张狗的图片,它判断是狗。
这两个判断过程互不影响。前一次的输入和输出,对后一次的判断没有任何帮助。这在很多场景下是没问题的。
但是,请思考以下任务:
阅读理解: "今天天气很好,我心情也很___。" 空格里很可能填“好”或“不错”。这个推断依赖于前面的“天气很好”。
语音识别: 当你听到一句话的开头,它会帮助你预测后面可能出现的音节。
股票预测: 今天的股价,很大程度上取决于昨天、前天乃至过去一段时间的走势。
这些任务的共同点是,它们处理的都是序列数据(Sequential Data)。序列中的数据不是独立的,前一个数据点包含了对理解后一个数据点至关重要的信息。
传统的神经网络缺乏记忆能力,无法处理这种时间上的依赖关系。而RNN,就是为了解决这个问题而生的。
结论:RNN是一种专门用于处理序列数据的神经网络,其设计的核心就是赋予网络一种“记忆”能力,让它能够捕捉序列中的时间依赖关系。
第二部分:RNN的核心结构
1. 折叠形式 (Folded):
,-----,| | <-- (代表信息的循环)'-----'^|x_t ---> [ A ] ---> o_t(输入) (RNN单元) (输出)[ A ]: 代表RNN的处理单元。
x_t: 代表在时间点
t的输入。o_t: 代表在时间点
t的输出。最重要的部分是那个指向自身的循环箭头: 它表示
A单元的输出结果(具体来说是隐藏状态h_t,我们稍后会讲)会作为下一次计算的输入,再次进入A单元。这就是“循环”或“记忆”的来源。
2. 展开形式 (Unfolded):
(初始记忆)h_(-1)|v... --> [ A ] --(传递记忆 h_0)--> [ A ] --(传递记忆 h_1)--> [ A ] --(传递记忆 h_2)--> ...| | |^ ^ ^| | |x_0 x_1 x_2 (序列输入)| | |v v vo_0 o_1 o_2 (序列输出)(t=0 时刻) (t=1 时刻) (t=2 时刻)让我们来详细解读一下这个结构:
x_t:这是在时间步(time step)t 的输入。比如,在处理一句话 "I am a student" 时,x_0 就是 "I",x_1 就是 "am",以此类推。
h_t:这是在时间步 t 的隐藏状态(Hidden State)。可以把它理解为RNN在时间点 t 的记忆。它不仅包含了当前输入x_t的信息,还包含了上一个时间步的隐藏状态h_t−1(也就是过去的记忆)的信息。
o_t:这是在时间步 t 的输出。比如,在做下一个词预测时,o_t 就是基于到x_t为止的所有信息,预测出的下一个最可能的词。
A:代表RNN的计算单元。重要的是,在所有时间步中,这个A是完全相同的。它包含的参数(权重矩阵)在整个序列处理过程中是共享的。这大大减少了模型的参数量,也让模型学会一种通用的处理规则,而不是为每个时间点都学一套新规则。
图中虽然画了多个
[ A ],但请记住,它们是同一个单元,拥有完全相同的参数(权重)。我们只是为了说明流程,把它在时间维度上复制了多份。
工作流程(前向传播):
初始状态:在 t=0 时,我们需要一个初始的隐藏状态 h_−1(通常初始化为全零向量)。
t=0 时刻:RNN单元接收初始隐藏状态 h_−1 和第一个输入 x_0。通过内部计算,它会生成新的隐藏状态(新的记忆)h_0,并可能产生一个输出 o_0。
t=1 时刻:RNN单元接收上一时刻的记忆 h_0 和当前输入 x_1。它将这两者结合,更新自己的记忆,生成新的隐藏状态 h_1,并输出 o_1。
循环往复:这个过程一直持续下去,直到序列的所有输入都被处理完毕。在每一步,h_t 都像一个“记忆胶囊”,携带着从序列开始到当前位置的所有重要信息,向下传递。
结论:RNN通过一个循环的隐藏状态(Hidden State),将过去的信息编码并传递到当前步骤,从而实现了对序列数据的记忆。
第三部分:深入RNN的数学原理
现在我们把那个黑盒子 "A" 打开,看看里面到底发生了什么计算。
在任意一个时间步 t,计算主要分为两步:
1. 更新隐藏状态 h_t:
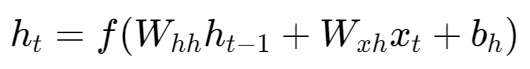
拆解这个公式:
h_t−1:上一时刻的隐藏状态(向量)。
x_t:当前时刻的输入(向量)。
W_hh:隐藏状态到隐藏状态的权重矩阵。它决定了“应该保留多少上一时刻的记忆”。
W_xh:输入到隐藏状态的权重矩阵。它决定了“应该从当前输入中吸收多少新信息”。
b_h:隐藏状态的偏置项(bias)。
f:激活函数。在RNN中,通常使用 tanh(双曲正切函数)。为什么用tanh?因为它能将输出值压缩到-1到1之间,这有助于控制信息流,防止梯度在网络中传播时变得过大或过小(尽管不能完全解决,后面会讲)。
2. 计算输出 o_t:
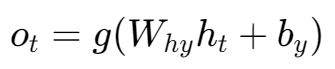
h_t:当前时刻刚刚计算出来的隐藏状态。
W_hy:隐藏状态到输出的权重矩阵。它决定了“如何利用当前的记忆来生成输出”。
b_y:输出的偏置项。
g:输出层的激活函数。这个根据具体任务决定。
如果是分类任务(比如情感分析),通常用 Softmax。
如果是回归任务(比如预测股价),可能就不用激活函数或用线性激活函数。
关键点:在整个训练过程中,模型要学习的就是这几个共享的权重矩阵(W_hh,W_xh,W_hy)和偏置项。无论序列有多长,它们都是同一套参数。
第四部分:RNN的训练与挑战
训练:BPTT算法
RNN的训练算法叫做通过时间的反向传播(Backpropagation Through Time, BPTT)。
还记得那个展开的RNN图吗?BPTT的原理其实很简单:
前向传播:按照我们上面讲的流程,从头到尾计算出所有时间步的隐藏状态和输出。
计算总损失:将每个时间步的输出 o_t 与真实标签 y_t 进行比较,计算损失(例如使用交叉熵损失),然后将所有时间步的损失相加,得到总损失。
反向传播:将总损失从最后一个时间步开始,沿着展开的图反向传播,计算每个权重矩阵的梯度。因为权重是共享的,所以每个时间步计算出的梯度会累加到对应的共享权重上。
更新权重:使用梯度下降法(如Adam, SGD等)根据累加后的总梯度来更新权重矩阵 W_hh,W_xh,W_hy。
长期依赖问题(Long-Term Dependencies)
这是简单RNN最致命的弱点。
想象这个句子:"I grew up in France... (此处省略很多文字)... therefore, I speak fluent French."
为了正确预测出 "French",模型需要记住很久以前的信息 "France"。
在BPTT过程中,梯度需要从序列末端一直传播回序列的开端。根据链式法则,这个梯度会不断地乘以权重矩阵 W_hh。
梯度消失(Vanishing Gradients):如果 W_hh 中的值(更准确地说是它的雅可比矩阵的范数)小于1,那么在多次连乘后,梯度会变得极其微小,趋近于0。这导致模型无法从遥远的过去学习到信息,长期记忆丢失。这是最常见也最棘手的问题。
梯度爆炸(Exploding Gradients):反之,如果 W_hh 中的值大于1,多次连乘后梯度会变得非常大,导致模型训练不稳定,参数更新幅度过大,甚至变成NaN。这个问题相对容易发现和解决(例如通过梯度裁剪 (Gradient Clipping) 来限制梯度的大小)。
由于梯度消失问题的存在,标准的RNN很难学习到超过5-10个时间步的依赖关系,这极大地限制了它的应用。
第五部分:解决方案与演进——LSTM与GRU
为了解决长期依赖问题,研究人员设计了更复杂的RNN变体,其中最成功、最流行的就是长短期记忆网络(Long Short-Term Memory, LSTM)和门控循环单元(Gated Recurrent Unit, GRU)。
它们的核心思想是引入门(Gate)的结构。
你可以把门想象成一个信息过滤器,它由一个Sigmoid激活函数和一个逐元素相乘操作组成。Sigmoid的输出在0到1之间,可以看作是一个开关:
输出为0,表示“完全关闭”,不允许任何信息通过。
输出为1,表示“完全打开”,让所有信息通过。
输出在0和1之间,表示“部分打开”,按比例让信息通过。
LSTM: 它引入了一个独立的细胞状态(Cell State),专门负责长距离传递信息。然后,它设计了三个精巧的门来控制细胞状态:
遗忘门(Forget Gate):决定应该从细胞状态中丢弃哪些旧信息。
输入门(Input Gate):决定哪些新信息应该被存入细胞状态。
输出门(Output Gate):决定细胞状态中的哪些信息应该被用作当前的输出。
通过这三个门的协同工作,LSTM可以明确地学习到何时遗忘、何时记忆、何时输出,从而有效地解决了梯度消失问题,能够捕捉非常长的序列依赖。
GRU: 这是LSTM的一个简化版,它将遗忘门和输入门合并为了一个更新门(Update Gate),并且没有独立的细胞状态。GRU的结构更简单,参数更少,计算效率更高,在许多任务上能达到和LSTM相近的效果。
明天我们讲解RNN的pytorch逐行实现以及LSTM与GRU的深入原理讲解
