当前位置：首页 > news >正文

2025年最新SCI-灰熊增脂优化器(Grizzly Bear Fat Increase, GBF)-附完整Matlab免费代码

news 2025/8/2 8:42:36

1、简介

本文介绍了一种新的受自然启发的优化算法，称为灰熊增脂优化器（GBFIO）。GBFIO算法模仿灰熊积累体脂为过冬做准备的自然行为，利用它们的狩猎、捕鱼和吃草、蜂蜜等策略。因此，GBFIO算法建模并考虑了三个数学步骤来解决最佳化问题：（1）根据过去的经验和嗅觉线索寻找食物来源（例如蔬菜、水果、蜂蜜、牡蛎）；（2）猎杀动物并保护后代免受捕食者的伤害；和（3）捕鱼。

2.灰熊增脂优化算法

首先，本节将描述GBFIO算法，接下来将说明其数学模型以优化各种优化问题。

2.1 GBFIO算法理论

熊必须在一年中温暖的月份在体内储存足够的脂肪，以便在冬眠和几个月不活动的寒冷月份养活自己。有幼崽的熊也必须在冬眠期间储存足够的脂肪来喂养幼崽，如果它们不能储存足够的脂肪，幼崽就会死亡。图1显示了一只灰熊和她的两只幼崽，它们正在进食并试图增加脂肪以在冬天生存。
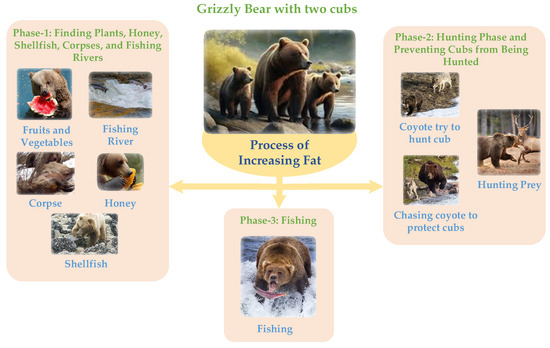
在这里插入图片描述
图1.一只灰熊带着两只幼崽和增加脂肪的过程。
灰熊是杂食动物，它们的饮食依赖于可获得的食物来源，除了捕鱼和狩猎，棕熊以水果、树根、贝类、蜂蜜等植物材料为食。
因此，灰熊脂肪的增加可分为以下三个阶段，每一步都在熊体内储存一些脂肪，直到达到冬眠所需的量（见图1）：（1）根据前几年的记忆和嗅觉，寻找蔬菜、水果、贝类、池塘、河流的位置进行捕鱼，并跟踪鱼的运动；（2）猎杀其他动物，同时也照顾后代，以避免被猎杀；（3）捕鱼（这是局部搜索）。因此，提出的基于灰熊脂肪增加的优化算法建模如下：

2.1.1第一阶段：寻找植物、蜂蜜、贝类、尸体和钓鱼河

灰熊增肥的主要饮食是鱼，但在鱼从海里到达产卵地和灰熊找到适合捕鱼的地方之前，它们吃其他东西，包括蔬菜、水果、蜂蜜、贝类和死去的动物尸体。因此，通过吃蔬菜、水果、贝类等来增肥，同时也找到鱼，模型如下：

$xbearsearch(t+1)=xbearsearch(t)+r1.Δxfish+r2.Δxhoney+r3.Δxshell+r4.Δxcorpse+r5.Δxplants(2)x_{\text{bear}}^{\text{search}}(t+1) = x_{\text{bear}}^{\text{search}}(t) + r_1. \Delta x_{\text{fish}} + r_2. \Delta x_{\text{honey}} + r_3. \Delta x_{\text{shell}} + r_4. \Delta x_{\text{corpse}} + r_5. \Delta x_{\text{plants}} \tag{2}$

$Δxfish=xfish−xbearsearch(t),(3)\Delta x_{\text{fish}} = x_{\text{fish}} - x_{\text{bear}}^{\text{search}}(t), \tag{3}$

$Δxhoney=xhoney−xbearsearch(t),(4)\Delta x_{\text{honey}} = x_{\text{honey}} - x_{\text{bear}}^{\text{search}}(t), \tag{4}$

$Δxshell=xshell−xbearsearch(t),(5)\Delta x_{\text{shell}} = x_{\text{shell}} - x_{\text{bear}}^{\text{search}}(t), \tag{5}$

$Δxcorpse=xcorpse−xbearsearch(t),(6)\Delta x_{\text{corpse}} = x_{\text{corpse}} - x_{\text{bear}}^{\text{search}}(t), \tag{6}$

$Δxplants=xplants−xbearsearch(t).(7)\Delta x_{\text{plants}} = x_{\text{plants}} - x_{\text{bear}}^{\text{search}}(t). \tag{7}$

其中 $xfishx_{\text{fish}}$ 、 $xhoneyx_{\text{honey}}$ 、 $xshellx_{\text{shell}}$ 、 $xcorpsex_{\text{corpse}}$ 和 $xplantsx_{\text{plants}}$ 是鱼、蜂蜜、贝壳、尸体和植物，熊试图找到这些食物以增加脂肪并度过冬季。 $xbearsearch(t)x_{\text{bear}}^{\text{search}}(t)$ 是当前种群，最好的五个种群被选为 $xfishx_{\text{fish}}$ 、 $xhoneyx_{\text{honey}}$ 、 $xshellx_{\text{shell}}$ 、 $xcorpsex_{\text{corpse}}$ 和 $xplantsx_{\text{plants}}$ 。当前迭代次数用 $t$ 表示。

此外，找到每种食物对熊来说都是具有挑战性的，并且是随机找到的， $r_1$ 到 $r_5$ 被定义为显示每种食物来源的随机状态，因此 $r_1$ 到 $r_5$ 被定义如下：

$r1s=2.rand.rand,(8)r_1^s = 2. \text{rand}. \sqrt{\text{rand}}, \tag{8}$

$r2s=rand.rand,(9)r_2^s = \text{rand}. \sqrt{\text{rand}}, \tag{9}$

$r3s=rand2.rand,(10)r_3^s = \frac{\text{rand}}{2}. \sqrt{\text{rand}}, \tag{10}$

$r4s=rand4.rand,(11)r_4^s = \frac{\text{rand}}{4}. \sqrt{\text{rand}}, \tag{11}$

$r5s=rand8.rand,(12)r_5^s = \frac{\text{rand}}{8}. \sqrt{\text{rand}}, \tag{12}$

其中 $rand\text{rand}$ 值在 [0, 1] 范围内随机选择。 $r_1$ 值比其他随机值大，因为鱼对熊来说是一种更有趣的食物，并且在脂肪增加方面具有高营养价值。因此，减少营养价值及其对增加脂肪的影响，其效应系数的值也减少，因此我们有 $r_1^s > r_2^s > r_3^s > r_4^s > r_5^s$ 。此外， $r_1^s$ 、 $r_2^s$ 、 $r_3^s$ 、 $r_4^s$ 和 $r_5^s$ 的值分别在 [0, 2]、[0, 1]、[0, 0.5]、[0, 0.25]、[0, 125] 范围内。

2.1.2. 狩猎阶段和保护幼崽免受捕猎

灰熊的一种增肥方式是通过捕猎其他动物获得的。母熊必须保持警惕，以保护幼崽免受潜在捕食者（包括郊狼和其他熊）的捕猎，这影响了狩猎过程。如果幼崽被杀，母熊在冬季需要更少的食物和脂肪，这也是模型的一部分。因此，狩猎熊的阶段如下。

作为第一步，熊识别它们的猎物并朝它们移动。由于模拟熊的行为，所提出的 SBFIO 在搜索空间中搜索以发现各种搜索区域。SBFIO 的一个关键特征是猎物在搜索空间中的位置是随机确定的。方程 (12) 模拟了熊如何移动到其目标以及这些概念如何工作。

$Δxbear=[2.r1b.xhuntnum(t)−r2b.xprey(t)],(13)\Delta x_{\text{bear}} = [2. r_1^b. x_{\text{hunt}}^{\text{num}}(t) - r_2^b. x_{\text{prey}}(t)], \tag{13}$

$xbearhunt(t+1)=xbearhunt(t)−A.Δxbear,(14)x_{\text{bear}}^{\text{hunt}}(t+1) = x_{\text{bear}}^{\text{hunt}}(t) - A. \Delta x_{\text{bear}}, \tag{14}$

其中 $r_1^b$ 和 $r_2^b$ 是在 [0, 1] 范围内随机选择的值。猎物越大，熊积累的脂肪越多；因此，为了最大化脂肪积累，最佳种群在前一更新步骤后获得，被选为猎物。所以， $xhuntnumx_{\text{hunt}}^{\text{num}}$ 是当前种群，其中被选为熊的种群，试图捕猎最佳猎物以增加其脂肪水平。 $xprey(t)x_{\text{prey}}(t)$ 是从前一步骤更新的种群中获得的最佳种群。 $A$ 表示通过方程 (14) 计算的系数向量。

$\alpha (2. r_3^b - 1), \tag{15}$

其中 $α\alpha$ 值在 [0, 2.5] 范围内线性从 2.5 减少到 0， $r_3^b$ 显示在 [0, 1] 范围内的随机值。

在第二步中，模拟了其他动物（包括郊狼）对幼崽的捕食。在这一步中，假设熊在狩猎过程中必须保护两个幼崽，以防止它们被捕猎。如果幼崽被猎杀，母熊因不喂养幼崽而储存更多脂肪。因此，当前种群，即母熊，如果幼崽被捕猎，则可以增加更多脂肪。从种群中随机选择三个个体作为幼崽和郊狼，并且，由于郊狼是捕食者并且比幼崽更强，这三个被选中的成员中最好的成员被选为郊狼，另外两个成员被选为幼崽。因此，用郊狼捕猎幼崽的模型如下：

$Δxcub-1cote=[2.r4b.xcub(1)−r5b.xcote(t)],(16)\Delta x_{\text{cub-1}}^{\text{cote}} = [2. r_4^b. x_{\text{cub}}^{(1)} - r_5^b. x_{\text{cote}}(t)], \tag{16}$

$Δxcub-2cote=[2.r6b.xcub(2)−r7b.xcote(t)],(17)\Delta x_{\text{cub-2}}^{\text{cote}} = [2. r_6^b. x_{\text{cub}}^{(2)} - r_7^b. x_{\text{cote}}(t)], \tag{17}$

$xbearcarr(t+1)=xbearcarr(t)−B1.Δxcub-1cote−B2.Δxcub-2cote(18)x_{\text{bear}}^{\text{carr}}(t+1) = x_{\text{bear}}^{\text{carr}}(t) - B_1. \Delta x_{\text{cub-1}}^{\text{cote}} - B_2. \Delta x_{\text{cub-2}}^{\text{cote}} \tag{18}$

$B1=B2=ρ(2.r8b−1),(19)B_1 = B_2 = \rho (2. r_8^b - 1), \tag{19}$

其中 $xcotecarr(t)x_{\text{cote}}^{\text{carr}}(t)$ 是在第一阶段更新后的种群中被选为母熊以保存和增加其身体的当前种群， $xcote(t)x_{\text{cote}}(t)$ 是在这三个被选中的成员中最好的成员， $xcub(1)x_{\text{cub}}^{(1)}$ 和 $xcub(2)x_{\text{cub}}^{(2)}$ 是在这三个被选中的成员中随机选择的三个成员。( $xcotex_{\text{cote}}$ 是这三个被选中成员中最好的成员，而其他两个成员被选为 $xcub(1)x_{\text{cub}}^{(1)}$ 、 $r_4^b$ 、 $r_5^b$ 、 $r_6^b$ 和 $r_7^b$ 是 [0, 1] 范围内的随机向量。 $B_1$ 和 $B_2$ 显示通过方程 (17) 计算的系数向量。其中 $ρ\rho$ 值在 [0, 1.25] 范围内，并且在迭代过程中线性从 1.25 减少到 0。

在本节中，假设熊要么狩猎和增肥，要么熊可以通过失去幼崽来储存更多脂肪。由于熊照顾幼崽，幼崽也可以通过逃跑和战斗来生存。熊更有可能被郊狼或其他熊捕猎，这影响了狩猎过程。考虑到这一点，狩猎状态被认为是幼崽被捕猎或丢失，因此我们有以下内容：

$β>0.7(20)x_{\text{bear}}^{\text{hunting-care}}(t+1) = \begin{cases} x_{\text{bear}}^{\text{hunt}}(t+1) & \text{if } \beta \leq 0.7 \\ x_{\text{bear}}^{\text{carr}}(t+1) & \text{if } \beta > 0.7 \end{cases} \tag{20}$

其中 $β\beta$ 是 [0, 1] 范围内的随机值。

2.1.3. 第三阶段：捕鱼

灰熊对鱼有很强的偏好。每年，成千上万的鲑鱼迁徙上游产卵。这些鱼为熊提供了它们需要生存的丰富脂肪和蛋白质。鱼的丰富性帮助熊获得它们需要度过冬季的体重。

灰熊沿着鲑鱼的迁徙路径定位自己，捕捉鱼并跃入河中。每只熊占据一个特定位置，并能够在半径 $r$ 内的一个圆形捕鱼区域内每天捕获一定数量的鱼。随着冬季的临近和结束，鱼的数量减少，熊的脂肪增加到冬眠所需的量。因此，我们对以下内容进行建模：

$xbearfishing(t+1)=(1+F).xbearfishing(t),(21)x_{\text{bear}}^{\text{fishing}}(t+1) = (1 + F). x_{\text{bear}}^{\text{fishing}}(t), \tag{21}$

$\eta \cdot \cos(2. \pi. r_1^f), \tag{22}$

其中 $xbearfishing(t)x_{\text{bear}}^{\text{fishing}}(t)$ 是第二阶段后更新的当前种群，对应于参与捕鱼以增加脂肪储备的熊。项 $cos⁡(2.π.r1f)\cos(2. \pi. r_1^f)$ 用于模拟圆形捕鱼区域，其中 $r_1^f$ 是 [0, 1] 范围内的随机值。参数 $η\eta$ 在 [0, 1] 范围内，表示在迭代过程中从 1 减少到 0 的衰减因子。衰减因子 $η\eta$ 设置为 0.3。

成年灰熊每天大约捕获 25 条鱼。为了考虑每日捕鱼量， $fnumf^{\text{num}}$ 是每只熊每天的捕鱼尝试（或重复）次数。因此，我们对捕鱼阶段表示如下：

$(xbearfishing(t+1))(f)=(1+fnum.ffishing(t))(f),∀f=[1,2,...,25],(23)(x_{\text{bear}}^{\text{fishing}}(t+1))^{(f)} = (1 + f^{\text{num}}. f^{\text{fishing}}(t))^{(f)}, \quad \forall f = [1, 2, ..., 25], \tag{23}$

其中最大数量 $γ\gamma$ 等于 25。一般来说，在捕鱼阶段，每只熊更新 25 次。每次钓鱼尝试后，如果新生成的解决方案（位置）产生更好的适应度值，它会替换前一个。在本节中，提出了GBFIO算法的执行过程，步骤如下：

步骤1：设置输入值，包括变量数量（n）、变量的最大值和最小值、最大迭代次数（Iter_max）和种群大小（N）。初始化建议的GBFIO算法参数，包括捕鱼数量（f = 25）和 $η=0.3\eta = 0.3$ 。最后，设置以下参数的最大数量： $α=2.5,ρ=1.25,γ=1\alpha = 2.5, \rho = 1.25, \gamma = 1$ 。

步骤2：在变量值范围内随机生成初始种群，如下所示：

$\bar{X}_{\text{pop}} = \text{rand}(1,n) * (X_{\text{max}} - X_{\text{min}}) + X_{\text{min}} \tag{22}$

其中 $XmaxX_{\text{max}}$ 和 $XminX_{\text{min}}$ 是变量的最小值和最大值。 $rand\text{rand}$ 显示 [0, 1] 范围内的随机向量。此外，计算每个种群的目标函数。因此，计算主要种群后，该过程对每个参数重复。

步骤3：开始迭代并将迭代次数设置为 $\text{iteration}$ 。

步骤4：开始搜索阶段，基于目标函数选择前5个最佳成员，如鱼、蜂蜜、贝壳、尸体和植物。根据方程 (1)-(11) 计算新的新搜索种群（每个种群被选为熊寻找食物）。

步骤5：计算步骤4中新计算种群的整个目标函数。如果每个新搜索种群的目标函数优于初始种群，则用步骤4中计算的新搜索种群更新初始种群。

步骤6：开始狩猎和护理阶段。

步骤6.1-狩猎阶段：从种群中选择表现最佳的成员作为猎物，这将为熊提供最多的脂肪。根据方程 (12)-(14) 计算整个新的狩猎种群。

步骤6.2-护理阶段：从种群中随机选择三个成员。在他们中，识别表现最佳的作为郊狼，其他两个作为熊幼崽。根据方程 (15)-(17) 计算新的熊种群。

步骤6.3-根据方程 (18) 选择狩猎和护理阶段的新种群。如果生成的随机数小于 0.7，则从狩猎阶段 (步骤 6.1) 选择新的狩猎和护理种群 ( $xbearhunting-carex_{\text{bear}}^{\text{hunting-care}}$ )；如果生成的随机数大于 0.7，则从护理阶段 (步骤 6.2) 选择狩猎和护理种群 ( $xbearnursing-carex_{\text{bear}}^{\text{nursing-care}}$ )。

步骤7：计算步骤 6.3 中新计算种群的整个目标函数。如果每个新的狩猎和护理种群 ( $xbearhunting-carex_{\text{bear}}^{\text{hunting-care}}$ ) 的目标函数优于更新后的初始种群，则用步骤 6 中计算的新狩猎和护理种群 ( $xbearhunting-carex_{\text{bear}}^{\text{hunting-care}}$ ) 替换种群。

步骤8：开始捕鱼阶段。每个更新的种群代表一只每天捕鱼 25 次的熊。将捕鱼次数设置为 $f = 1$ 。

步骤8.1：通过方程 (21) 计算新的捕鱼种群，然后计算目标函数。

步骤8.2：如果每个捕鱼种群 ( $xbearfishingx_{\text{bear}}^{\text{fishing}}$ ) 的目标函数优于更新后的初始种群，则用新的捕鱼种群 ( $xbearfishingx_{\text{bear}}^{\text{fishing}}$ ) 替换种群。

步骤8.3：如果捕鱼次数小于最大捕鱼次数 (25)，则将捕鱼次数 $f = f + 1$ 并返回步骤 8.1。否则，转到步骤 9。

步骤9：如果迭代次数小于最大迭代次数，则转到步骤 4；否则转到步骤 10。

步骤10：选择更新种群中的最佳成员作为解决方案，然后结束过程。

提出的GBFIO算法的伪代码在表 1 中描述。此外，GBFIO算法的流程图如图 2 所示。

```matlab
clc
clear all
pack
%%%%%%%%%% n is dimension of objective function
n = 30;
%%%%%%%%%% Define the Range of Variables
Xmax = ones(1,n) *100;
Xmin = ones(1,n)*(−100);
%%%%%%%%%% n is the Population Size
N = 150;
%%%%%%%%%% Maximum Number of Iteration
Iter_max = 500;
%%%%%%%%%% Define the GBFIO parameters
f = 2.5;
eta = 1.25;
Zeta = 0.3;
fishing_number = 25;
%%%%%%%%%% Generate the Initial Populations
for i = 1:NIpop(i,:) = rand(1,n).*(Xmax − Xmin) + Xmin;cost(i,:) = sum(Ipop(i,:).^2);
end
%%%%%%%%%% Sort the Initial Populations Based on Cost Function
Ipop_mix = [Ipop,cost];
Ipop_sort = sortrows(Ipop_mix,n + 1);
%%%%%%%%%% Specify the Fish, Honey, Body, Shell, and Plants
Fish = Ipop_sort(1,:);
Honey = Ipop_sort(2,:);
Body = Ipop_sort(3,:);
Shell = Ipop_sort(4,:);
Plants = Ipop_sort(5,:);
%%%%%%%%%% Start the Iteration for Updating Populations
for iter = 1:Iter_maxfor i = 1:N%%%%%%%%%% Start the Searching Phaser1 = rand(1,n);deltax_fish = (2.*r1.*( (r1).^0.5)).*(Fish(1,[1:n]) − Ipop(i,:));deltax_honey = (r1.*((r1).^0.5)).*(Honey(1,[1:n]) − Ipop(i,:));deltax_body = (0.5.*r1.*((r1).^0.5)).*(Body(1,[1:n]) − Ipop(i,:));deltax_shell = (0.25.*r1.*((r1).^0.5)).*(Shell(1,[1:n]) − Ipop(i,:));deltax_plants = (0.125.*r1.*((r1).^0.5)).*(Plants(1,[1:n]) − Ipop(i,:)); Xnew_search = Ipop(i,:) + deltax_fish + deltax_honey + deltax_body + deltax_shell + deltax_plants;Xnew_search = min(Xnew_search,Xmax);Xnew_search = max(Xnew_search,Xmin);cost_S = sum(Xnew_search.^2);%%%%%%%%%% Update the Populationif cost_S < cost(i,1)Ipop(i,:) = Xnew_search;cost(i,1) = cost_S;end%%%%%%%%%% End the Searching Phase%%%%%%%%%% Start the Hunting Phase%%%%% Start the Hunting Phase: Bear HuntingIpop_mix = [Ipop,cost];Ipop_sort = sortrows(Ipop_mix,n + 1);Prey = Ipop_sort(1,:);A = (f*(1-iter/Iter_max)).*(2.*rand(1,n) − 1);D = abs(((2.*rand(1,n)).*Ipop(i,:))-(rand(1,n).*Prey(1,[1:n])));X_hunt = Ipop(i,:)-A.*D;X_hunt = min(X_hunt,Xmax);X_hunt = max(X_hunt,Xmin);cost_hunt = sum(X_hunt.^2);%%%%% Start the Hunting Phase: Coyote HuntingL = randperm(N);LL = find(L~ = i);LLL = L(LL);J1 = LL(1);J2 = LL(2);J3 = LL(3);I_child = [Ipop(J1,:),cost(J1,1);Ipop(J2,:),cost(J2,1);Ipop(J3,:),cost(J3,1)];I_chsort = sortrows(I_child,n + 1);A1 = (eta*(1-iter/Iter_max)).*(2.*rand(1,n) − 1);A2 = (eta*(1-iter/Iter_max)).*(2.*rand(1,n) − 1);D1 = abs(((2.*rand(1,n)).*I_chsort(2,[1:n])) − (rand(1,n).*I_chsort(1,[1:n])));D2 = abs(((2.*rand(1,n)).*I_chsort(3,[1:n])) − (rand(1,n).*I_chsort(1,[1:n])));X_ch = Ipop(i,:) − (A1.*D1 + A2.*D2);X_ch = min(X_ch,Xmax);X_ch = max(X_ch,Xmin);cost_ch = sum(X_ch.^2);%%%%%%%%%% Update the PopulationG = rand(1,1);if G < 0.75if cost_hunt < cost(i,1)Ipop(i,:) = X_hunt;cost(i,1) = cost_hunt;endelseif cost_ch < cost(i,1)Ipop(i,:) = X_ch;cost(i,1) = cost_ch;endend%%%%%%%%%% End the Hunting Phase%%%%%%%%%% Start the Fishing Phasefor kk = 1:fishing_numberZ = Zeta*(1 − iter/Iter_max)*cos(2*pi*rand(1,1));X_fish = (1 + Z).*Ipop(i,:);X_fish = min(X_fish,Xmax);X_fish = max(X_fish,Xmin);cost_fishing = sum(X_fish.^2);%%%%%%%%%% Update the Populationif cost_fishing < cost(i,1)Ipop(i,:) = X_fish;cost(i,1) = cost_fishing;endend%%%%%%%%%% Specify the Fish, Honey, Body, Shell, and Plants forIpop_mix = [Ipop,cost];Ipop_sort = sortrows(Ipop_mix,n + 1);Fish = Ipop_sort(1,:);Honey = Ipop_sort(2,:);Body = Ipop_sort(3,:);Shell = Ipop_sort(4,:);Plants = Ipop_sort(5,:);end%%%%%%%%%% Specify the Parameters of Convergence CurveConvergence_Curve(iter,1) = iter;Convergence_Curve(iter,2) = Ipop_sort(1,n + 1);
end
%%%%%%%%%% Print the Best Solution
Best = Ipop_sort(1,:);
plot(Convergence_Curve(:,1),Convergence_Curve(:,2))

Dehghani M, Aly M, Rodriguez J, Sheybani E, Javidi G. A Novel Nature-Inspired Optimization Algorithm: Grizzly Bear Fat Increase Optimizer. Biomimetics (Basel). 2025 Jun 7;10(6):379. doi: 10.3390/biomimetics10060379

查看全文

http://www.lryc.cn/news/605521.html