统计学08：概率分布

一、随机变量

随机变量是一个将 随机事件 映射到 数值 的数学函数，用于描述事件的结果。随机变量可以是离散的（如骰子）或连续的（如人的身高、体重）。

1）概率质量函数PMF——离散随机变量

        P(X = x) = 对应于某个值 ( x 的概率）

2）概率密度函数PDF——连续随机变量

        f(x) 描述随机变量在某点的概率密度。连续变量的概率在区间上求和：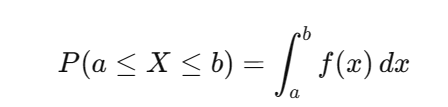

3）累计分布函数CDF：表示随机变量小于或等于某值的累计概率：

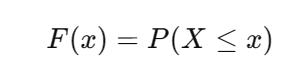
F(x) 对离散变量是 PMF 的累加，对连续变量是 PDF 的积分。

二、随机变量的期望和方差

明确了公式之后，就需要描述出来。既然概率是一个分布，那么使用期望与方差描述

2.1 期望

反映随机变量的平均值，用于衡量其中心位置

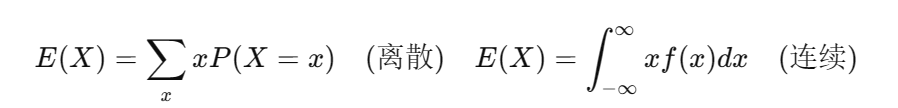
2.2 方差

衡量随机变量的分布范围或波动大小

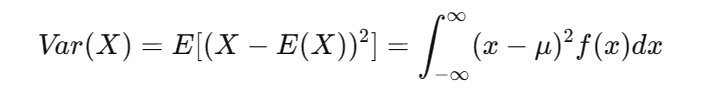
2.3 协方差和相关系数

描述两个随机变量之间的关系

2.4 正态分布中期望和方差的图形

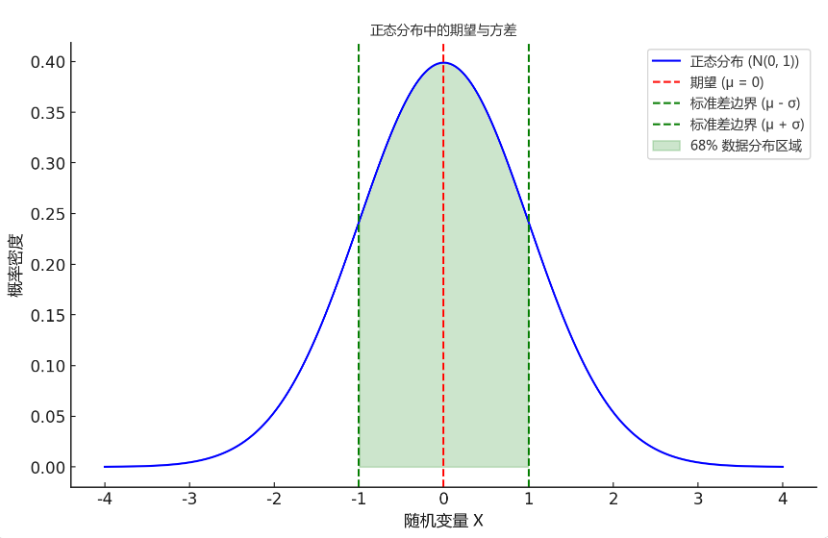
真实场景下：如果想要说明留存率50%是合理的还是不合理的。可以看他的分布，用期望去描述分布，方差去衡量变化。

三、多维随机变量与联合分布

如在参加活动的基础上，描述【历史有参加活动且有付费行为的用户】再次参加活动的概率。就涉及到了多维变量和联合分布相关

3.1 多维随机变量的定义

1）联合分布

联合概率 P(X=x,Y=y)（离散型） 或 联合概率密度函数 f(x,y)（连续型），描述两个或多个变量的联合行为。公式：

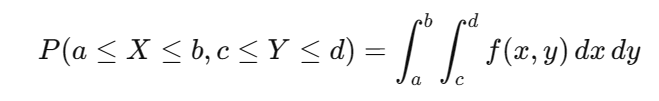
2）边缘分布

从联合分布中提取单个变量的分布。例如 fX​(x)

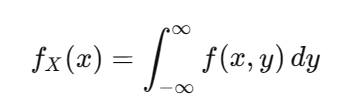
3）条件分布

在已知条件下计算变量的概率分布。例如 P(X∣Y=y) 或 f(X∣Y)

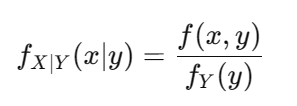
4）条件均值

联合正态分布下，给定 Y=y0​ 时，X 的条件均值 E(X∣Y=y0​) 可以表示为

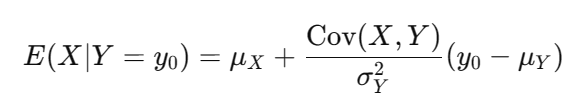
5）协方差和相关系数

协方差描述两个变量是否相关

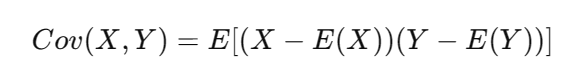
相关系数标准化协方差，取值范围为 [-1, 1]

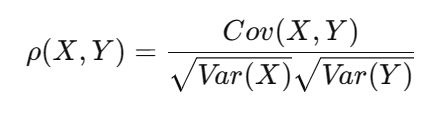
总结：概率分布是对事件过程的描述，因此不仅要拆解指标维度（比如分城市、用户层级），拆解订单量。对于留存率类的指标，也需要查看分布。描述概率分布，能清楚知道中间发生了什么。