当前位置：首页 > news >正文

数据结构自学Day13 -- 快速排序--“分而治之”

news 2025/7/25 20:51:45

🔶 一、快速排序（Quick Sort）

📌 基本思想：

分而治之：

每次从数组中选一个“基准”（pivot），把比它小的放左边，大的放右边。

对左右子数组递归排序。

🧠 排序过程：

选择一个基准（如第一个或最后一个元素）。
使用双指针或 Lomuto/Hoare 分区法将数组分为左右两部分。
对左右子数组递归调用快速排序。

⏱️ 时间复杂度：

情况	时间复杂度
最好情况	O(n log n)
平均情况	O(n log n)
最坏情况	O(n²)（当数组几乎有序或元素都相同时）

♻️ 稳定性：

不稳定排序

✅ 优点：

速度快：在大多数实际情况下性能极佳。
原地排序：不需要额外内存。
几乎是排序算法中的性能王者（除非你特别追求稳定性）。

❌ 缺点：

最坏情况下可能退化为 O(n²)。当我们选择的基准为最大元素或者最小元素
递归层数深时可能栈溢出（需优化）。
算法思维：
选择基准值，利用双指针遍历数组，将比基准值小的放置左边，比基准值大的放置右边。
思维导图：

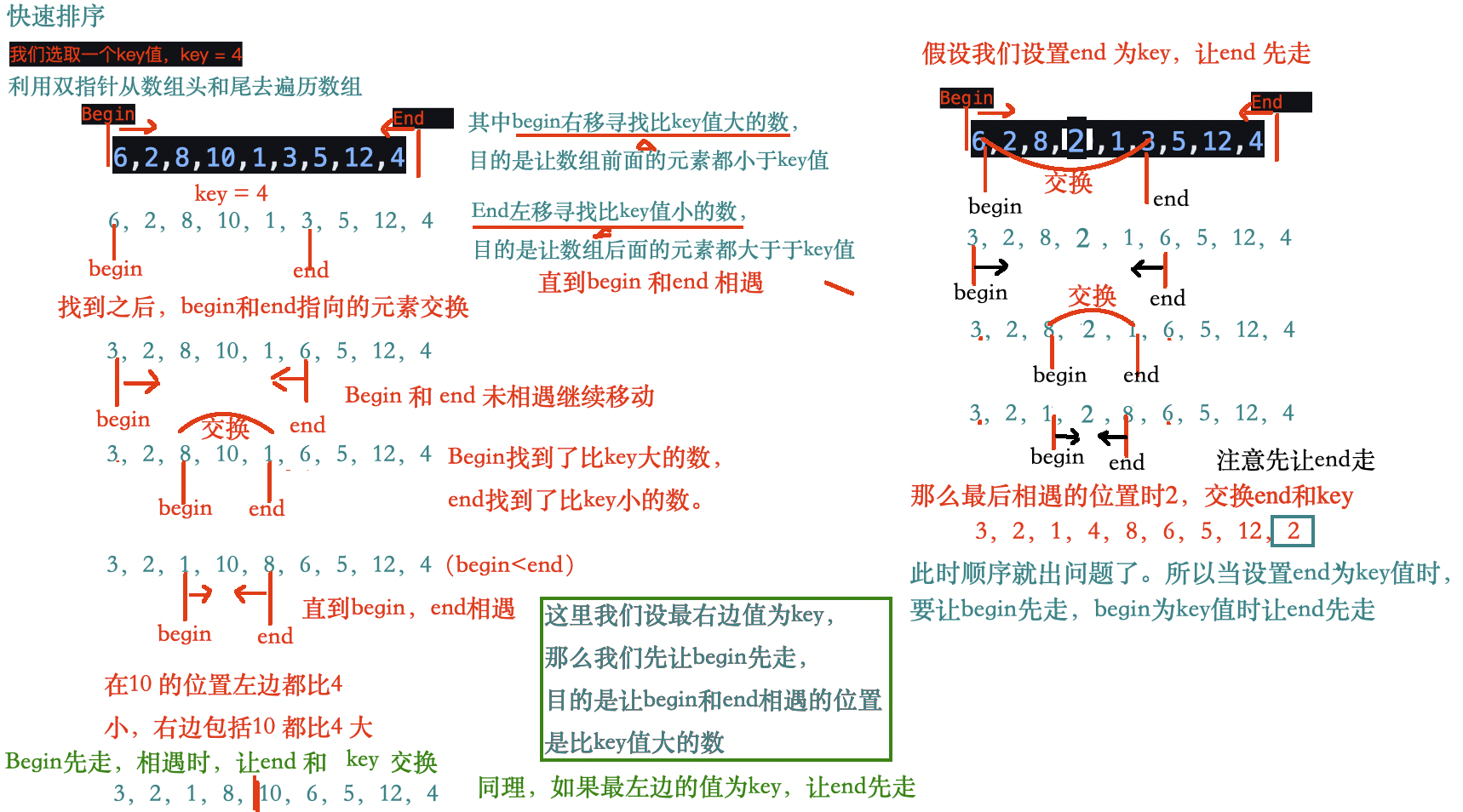
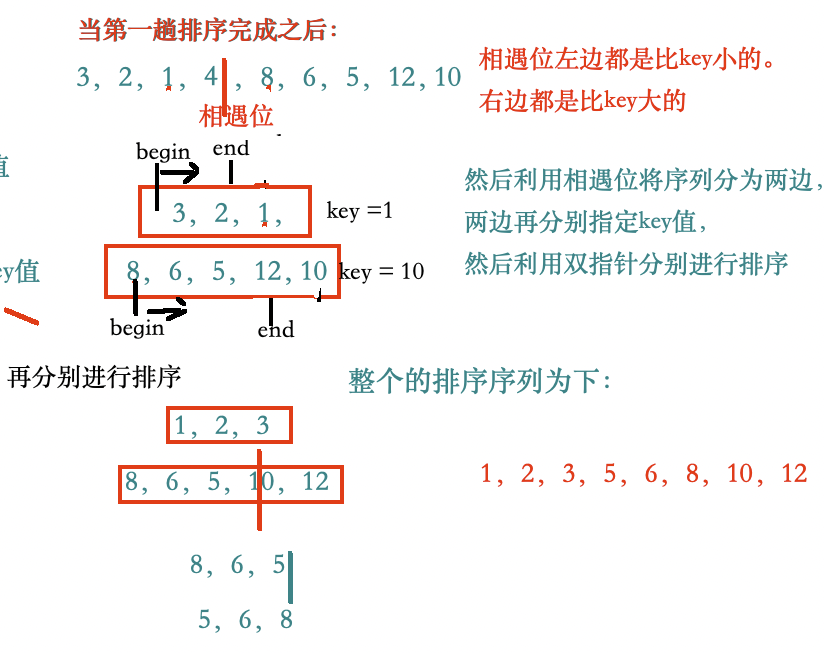
代码实现：


int PartSort(int* arr,int left,int right){assert(arr);int key_index = right;int begin = left;int end = right;while (begin< end){ while(begin < end && arr[begin] <= arr[key_index]){begin++;}while(begin < end && arr[end] >= arr[key_index]){end--;}Swap(&arr[begin],&arr[end]);}Swap(&arr[key_index],&arr[begin]);return begin;
}
void QuickSort(int* arr,int left,int right){assert(arr);if(left<right){int div = PartSort(arr,left,right);QuickSort(arr,left,div-1);QuickSort(arr,div+1,right);}
}

注意⚠️：

快速排序如果选择的基准值（key）如果为序列中的最大最小元素时，需要开辟非常多的栈，非常容易导致栈溢出，以及时间复杂度也会更高，最高为 $O(N^2)$ 。所以为此要避免选取最大元素或者最小元素，比如有序序列时。

快速排序改进方法：

“三数取中”：保证不要选到最小或者最大，让有序时最为优；

思维导图：

代码实现：

//三数取中优化
int get_midindex(int*arr,int left,int right){assert(arr);int mid = left+(right-left)/2;if(arr[left]>= arr[mid] && arr[left]<=arr[right] || arr[left]<= arr[mid] && arr[left]>=arr[right]){return left;}else if(arr[mid]>= arr[left] && arr[mid]<=arr[right] || arr[mid]<= arr[left] && arr[mid]>=arr[right]){return mid;}else{return right;}}