当前位置：首页 > news >正文

数据结构系列之AVL树

news 2025/7/25 20:55:12

前言

AVL树是为了解决搜索二叉树退化成链的问题，叫AVL树是因为发明者G. M. Adelson-Velsky和E. M. Landis 取首字母来的。

AVL树重要吗？其实很重要，因为他的旋转在红黑树中仍然会出现，但他仍然有缺陷，不然C++的map和set底层就不会是红黑树了。

一、什么是AVL树

AVL树仍然是一颗搜索二叉树，但他和普通的搜索二叉树的区别就是有一条规则：任意结点的左右子树的高度不会超过一，通过这一条规则来维护这颗树相对比较满。这样如果有N个结点，他的高度可维护在logN，插入的复杂度也在O(logN)

二、模拟

AVL实现的方法比较多，但是比较好理解的是利用平衡因子来控制，同时每一个结点维护三叉链（左右孩子和父亲），平衡因子怎么算？右子树的高度减去左子树的高度，既然满足这个条件，他的平衡因子只有三种可能：1/ - 1 / 0，插入会有变化就要去改。

这里模拟只模拟插入的过程，因为删除过于麻烦，也只是为了了解AVL。

节点定义：

前面已经讲了是三叉链结构，直接写成KV结构了

template<class K,class V>
struct AVLTreeNode {AVLTreeNode<K,V>* _left;AVLTreeNode<K,V>* _right;AVLTreeNode<K,V>* _parent;pair<K, V> _kv;int bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),bf(0),_left(nullptr),_right(nullptr),_parent(nullptr){}};

这里的bf就是平衡因子，balance factor,节点没啥讲的。

插入

插入可以分为两步：1.像搜索树一样插入。
2.维护平衡因子，根据平衡因子的状态进行旋转

非旋转

第一步：

bool insert(const pair<K, V>& kv)
{if (_root == nullptr){Node* newnode = new Node(kv);_root = newnode;return true;}else{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//找到了cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;
}

第二步：
插入之后会有几种情况？会不会影响父亲的平衡因子？
来用一张图分析一下：
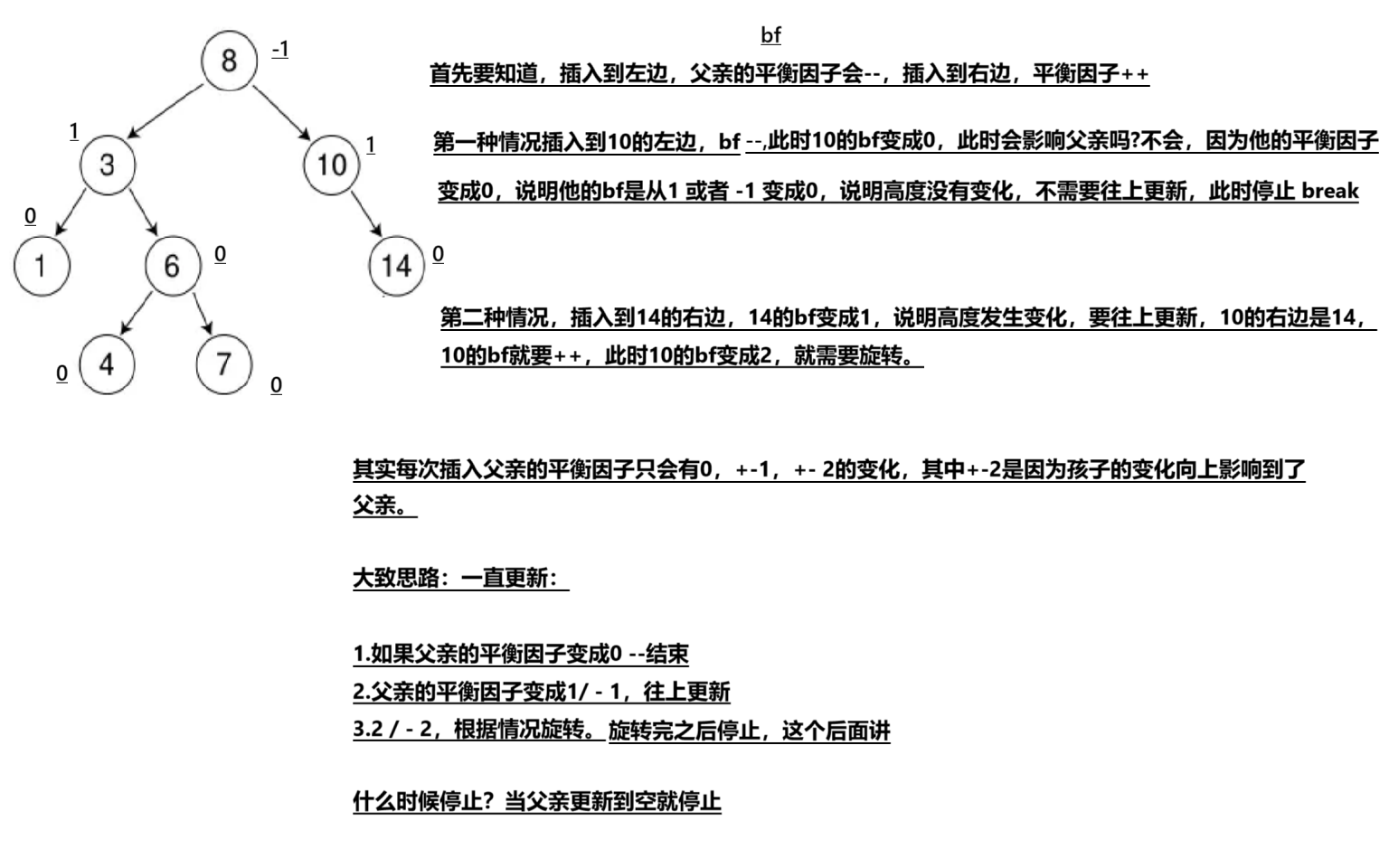
在这里插入图片描述
先把非旋转部分的写了

while (parent)
{if (parent->_left == cur){parent->bf--;}else{parent->bf++;}if (parent->bf == 0){//更新结束break;}else if (parent->bf == 1 || parent->bf == -1){//继续更新cur = parent;parent = cur->_parent;}else if(parent->bf == 2 || parent->bf == -2){//旋转break;}

旋转：

一共几种情况？四种，2 * 2，父亲是2 或者 -2，孩子是1 或者 - 1
画图先看比较简单的两种情况，右单旋和左单旋，因为这两种情况对称，只分析一种：
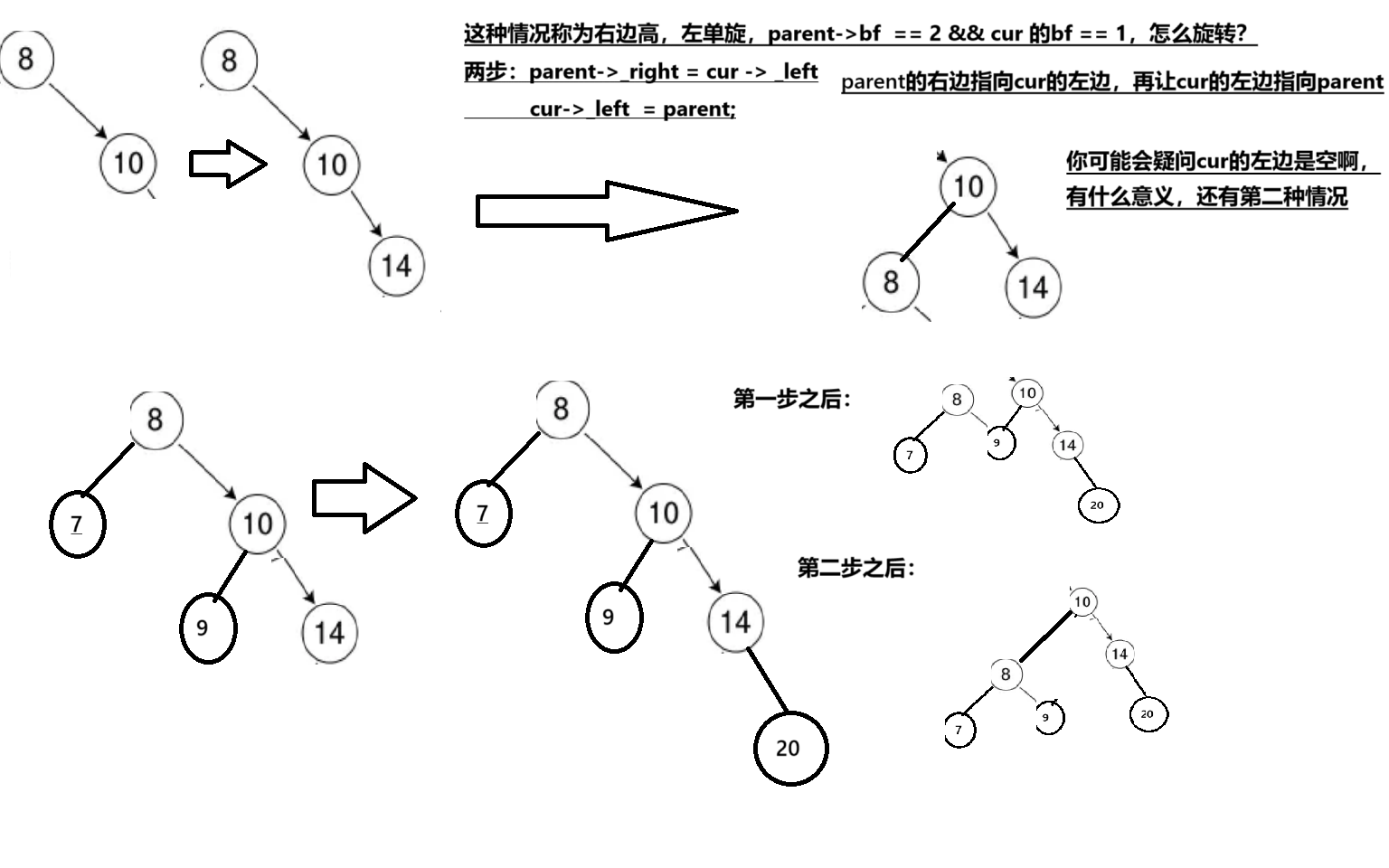
在这里插入图片描述
这么旋转之后变得平衡了，那代码好不好写呢？要考虑的因素有很多,特别是父子关系，最重要的是考虑图里的8有没有父亲，如果没有，让10变成根，如果有，还需要相连。

if (parent->bf == 2 && cur->bf == 1)
{RotateLeft(parent);//左单旋，右边高
}
void RotateLeft(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;//核心1if (curleft != nullptr){curleft->_parent = parent;}cur->_left = parent;//核心2 Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->bf = parent->bf = 0;
}

对称的情况

else if (parent->bf == -2 && cur->bf == -1)
{RotateRight(parent);//左边高，右单旋
}
void RotateRight(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright){curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->bf = parent->bf = 0;
}

双旋的情况：
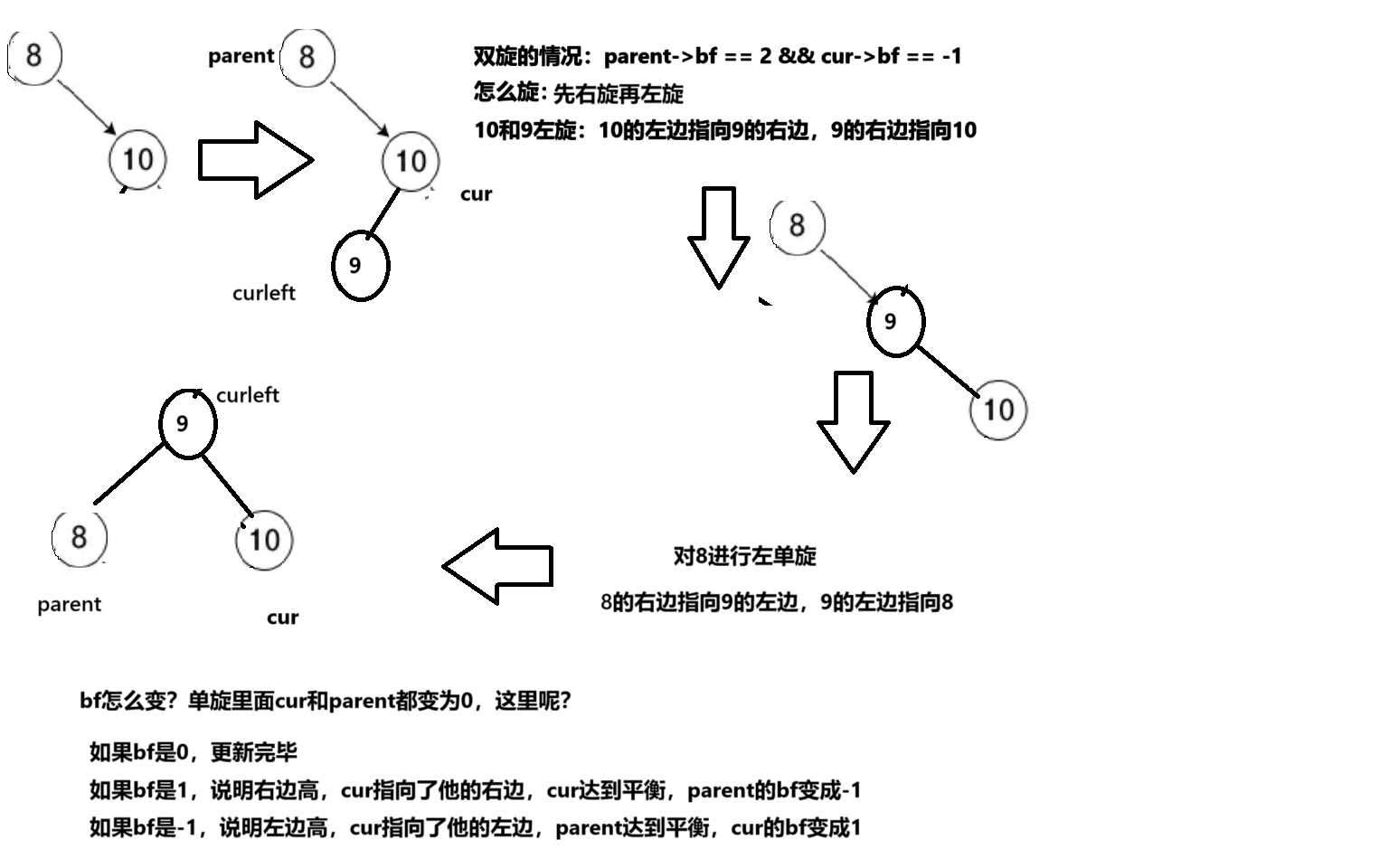
在这里插入图片描述

else if (parent->bf == 2 && cur->bf == -1)
{//折线形状//进行右左双旋RotateRightLeft(parent);
}
else if (parent->bf == -2 && cur->bf == 1)
{RotateLeftRight(parent);
}
void RotateLeftRight(Node* parent)
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->bf;RotateLeft(parent->_left);RotateRight(parent);if (bf == 0){return;}else if (bf == 1){cur->bf = -1;}else if (bf == -1){parent->bf = 1;}else{assert(false);}
}
void RotateRightLeft(Node* parent)
{Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->bf;RotateRight(parent->_right);RotateLeft(parent);if (bf == 0){return ;}else if (bf == 1){parent->bf = -1;}else if(bf == -1){cur->bf = 1;}else{assert(false);}
}

这就是AVL树的插入了。

三、验证正确性

1.验证他是搜索树，可以走一个中序遍历

void _Inorder(Node* node)
{if (node == nullptr){return;}_Inorder(node->_left);cout << node->_kv.first << ' ' << node->_kv.second << ' ' << endl;_Inorder(node->_right);}

2.验证他是AVL树，可以层序遍历大致看看对不对

void _LevelOrder(Node* node)
{queue<Node*> dq;if (_root != nullptr)dq.push(_root);size_t LevelSize = 1;while (!dq.empty()){for (size_t i = 0; i < LevelSize; ++i){Node* front = dq.front();cout << front->_kv.first << ' ';dq.pop();if (front->_left){dq.push(front->_left);}if (front->_right){dq.push(front->_right);}}LevelSize = dq.size();cout << endl;}
}

最严谨的验证方式还是计算每一个节点的bf和他存储的bf相不相等。

bool IsBalance()
{return _IsBalance(_root);
}
bool _IsBalance(Node* root)
{//判断是否平衡if (root == nullptr)return true;int leftH = Height(root->_left);int RightH = Height(root->_right);if (RightH - leftH !=  root -> bf){cout << "平衡因子异常" << endl;cout << root->_left << endl;return false;}return abs(RightH - leftH) < 2 && _IsBalance(root->_left) && _IsBalance(root->_right);
}
int Height(Node* node)
{if (node == nullptr) return 0;int leftH = Height(node->_left);int rightH = Height(node->_right);return leftH > rightH ? leftH + 1 : rightH + 1;
}

四、AVL的缺陷

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即logN但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数
据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合，整体还是不太常用的。

正因为AVL树过于严格，所以搞出来一颗红黑树来适当放宽限度，他也是map和set的底层。