数据结构自学Day13 -- 快速排序--“前后指针法”
快速排序的 “前后指针法”(也称为“Hoare划分方案”或“双指针遍历法”)是一种实现 partition(划分) 的思路,它与“挖坑法”不同,利用两个指针分别扫描元素并交换,从而实现原地划分。
往期“快速排序算法回顾”:
快速排序--挖坑法
快速排序-- 分而治之
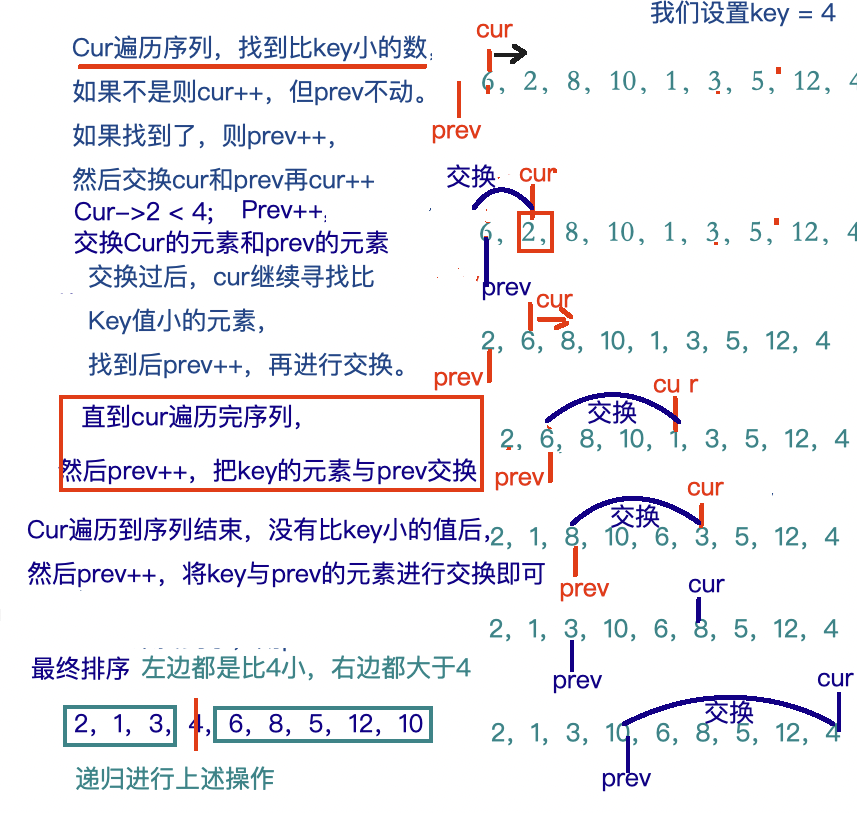
🧠 “前后指针”思想
“前后指针法”指的是:
用两个指针(cur 和 prev),一个扫描数组,一个标记小于 pivot 的“边界”,通过遍历和交换,把比 pivot 小的元素移到前面,比 pivot 大的放后面,最后把 pivot 放到中间。
🧩 思路详解
假设存在一个数组
-
数组为 arr[left..right];
-
选择 arr[right] 为基准值(pivot);
-
prev 初始化为 left - 1,指向已处理的最后一个小于 pivot 的元素;
-
cur 从 left 开始遍历到 right - 1,用于寻找比pivot小的元素。
🤔思维导图
代码实现
int PartSort3(int* arr,int left,int right){assert(arr);int mid_index = get_midindex(arr,left,right);Swap(&arr[mid_index],&arr[right]);int key = arr[right];int prev = left-1;for(int cur = left;cur<right;++cur){if(arr[cur]<key){prev++;Swap(&arr[cur],&arr[prev]);}}//可选while循环// while (cur< right){// if(arr[cur]<key)// {// prev++;// Swap(&arr[cur],&arr[prev]);// }// cur++;// }prev++;Swap(&arr[right],&arr[prev]);return prev; }
快速排序算法总结:
-
分而治之的排序思想(标准快排)
-
挖坑法(Hoare分区法)
-
前后指针法(Lomuto分区法)
它们本质上都基于快速排序的“分而治之”思想,但实现方式不同,影响效率与处理方式也有所区别。
| 实现方式 | 本质思想 | 分区原理 | 枢轴选取 | 优势 | 劣势 | 适用场景 |
|---|---|---|---|---|---|---|
| 分而治之 | 框架思想 | 递归分为左右两部分 | 自由选择 | 算法核心思维,通用 | 本身不包含具体实现 | 统一指导各类快排 |
| 挖坑法 | Hoare 分区法 | 左右指针互相填坑 | 一般选最左 | 交换少,性能好 | 易错,不能选两端作为枢轴 | 重复元素较多,追求效率 |
| 前后指针法 | Lomuto 分区法 | 逐个遍历,用前后指针交换 | 一般选最右 | 逻辑清晰,容易写 | 交换次数多,性能略逊 | 学习入门、小数据或调试 |