《 java 随想录》| 数组
前言:这是专门针对java语言讲解的算法解析(题目顺序参考代码随想录)


思维导图
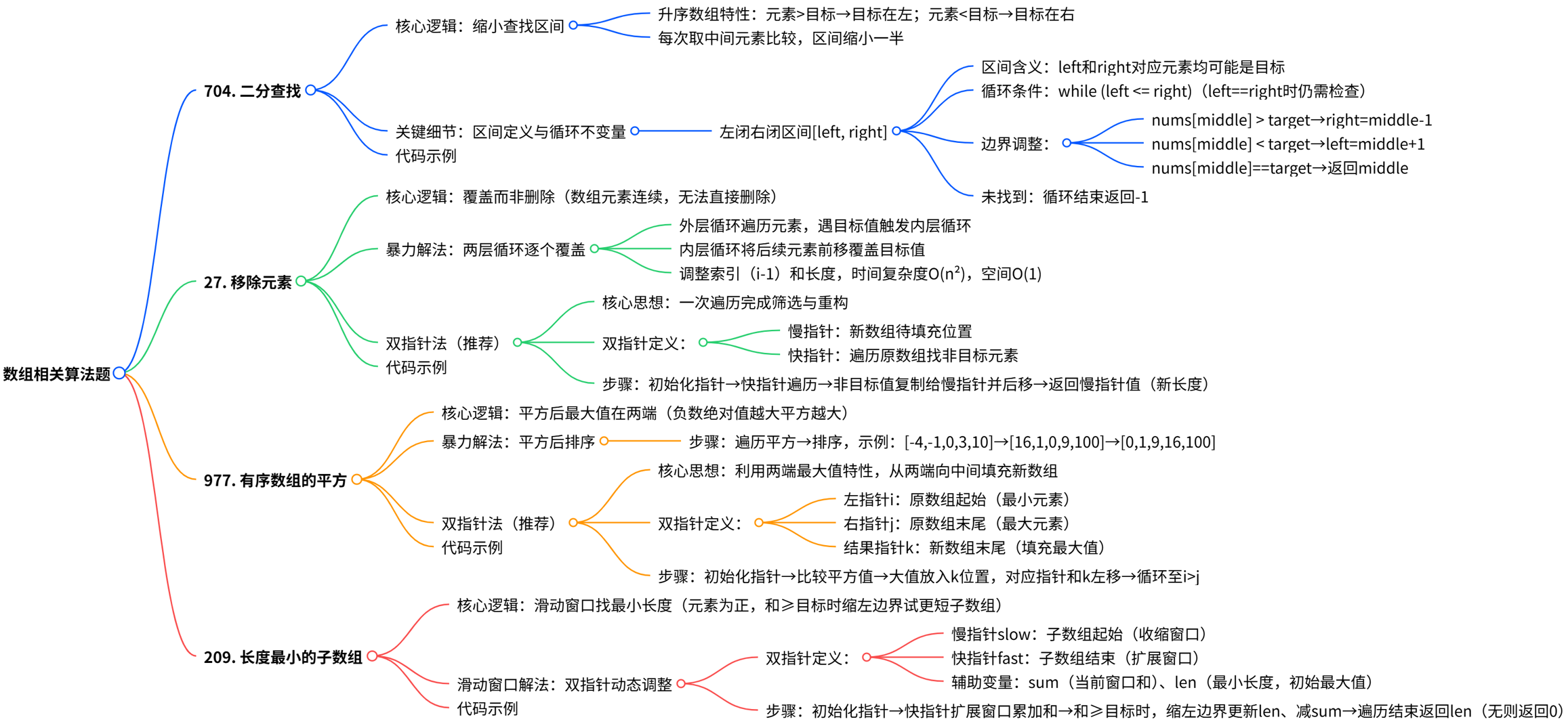
704. 二分查找

一、核心逻辑:缩小查找区间
数组是升序排列的,这意味着:
- 如果某元素大于目标值,那么目标值一定在该元素的左侧;
- 如果某元素小于目标值,那么目标值一定在该元素的右侧。
利用这个特性,我们可以每次选取区间中间的元素与目标值比较,从而将查找区间缩小一半,直到找到目标值或确认其不存在。
二、关键细节:区间定义与循环不变量
二分法的难点在于边界处理,而边界处理的核心是明确区间的定义。只要在整个查找过程中严格遵守区间的定义(即 “循环不变量”),就能避免逻辑混乱。
解法:左闭右闭区间 [left, right]
- 区间含义:查找的范围是从
left到right,且left和right对应的元素都可能是目标值。 - 循环条件:
while (left <= right)
因为当left == right时,区间[left, right]仍有一个元素需要检查,所以循环继续。 - 边界调整:
- 若
nums[middle] > target:目标值一定在middle左侧,因此右边界调整为right = middle - 1(排除middle)。 - 若
nums[middle] < target:目标值一定在middle右侧,因此左边界调整为left = middle + 1(排除middle)。 - 若
nums[middle] == target:直接返回middle(找到目标)。
- 若
- 未找到的情况:当循环结束(
left > right),说明整个区间已排查完毕,返回-1。
三、代码示例:
class Solution {public int search(int[] nums, int target) {// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算if (target < nums[0] || target > nums[nums.length - 1]) {return -1;}int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + ((right - left) >> 1);if (nums[mid] == target) {return mid;}else if (nums[mid] < target) {left = mid + 1;}else { // nums[mid] > targetright = mid - 1;}}// 未找到目标值return -1;}
}27. 移除元素

一、核心逻辑:覆盖而非删除
数组的元素在内存中是连续排列的,无法直接删除某个元素,只能用后续元素覆盖掉目标元素。因此,解题的关键在于:如何高效地将不需要删除的元素移动到数组前面,并确定新数组的长度。
二、暴力解法:两层循环逐个覆盖
思路:遍历数组,每遇到一个等于目标值的元素,就将其后所有元素向前移动一位。
- 外层循环:遍历数组中的每个元素。
- 发现目标值:当遇到等于
val的元素时,执行内层循环。 - 内层循环:将该元素之后的所有元素向前移动一位(覆盖掉当前元素)。
- 调整索引和长度:由于元素前移,当前索引
i需要减 1(回退一位),同时数组长度减 1。
时间复杂度:O(n2),因为每次删除元素需要移动后续所有元素。
空间复杂度:O(1),仅使用常数额外空间。
三、双指针法:高效覆盖(推荐)
核心思想:使用快慢指针在一次遍历中完成元素筛选和数组重构。
双指针定义:
- 慢指针:指向新数组中下一个元素的位置(即待填充位置)。
- 快指针:遍历原数组,寻找所有不等于
val的元素。
步骤:
- 初始化指针:
slow和fast均从 0 开始。 - 遍历数组:快指针
fast逐个检查元素。 - 筛选元素:若
nums[fast] != val,将其复制到nums[slow],并将slow后移一位。 - 返回结果:遍历结束后,
slow的值即为新数组的长度。
时间复杂度:O(n),只需一次遍历。
空间复杂度:O(1),仅使用常数额外空间。
四. 代码示例
class Solution {public int removeElement(int[] nums, int val) {// 快慢指针int slowIndex = 0;for (int fastIndex = 0; fastIndex < nums.length; fastIndex++) {if (nums[fastIndex] != val) {nums[slowIndex] = nums[fastIndex];slowIndex++;}}return slowIndex;}
}977. 有序数组平方和

一、核心逻辑:平方后的最大值在两端
由于原数组按非递减顺序排列,负数部分平方后可能成为较大值,但负数的绝对值越大,平方后的值越大。因此,平方后的最大值一定出现在原数组的两端(最左边或最右边),而不是中间。
二、暴力解法:平方后排序
思路:遍历数组,将每个元素平方,然后对整个数组进行排序。
步骤:
- 遍历数组:将每个元素替换为其平方值。
- 排序:对平方后的数组进行排序(如快速排序)。
示例: 原数组 [-4,-1,0,3,10] → 平方后 [16,1,0,9,100] → 排序后 [0,1,9,16,100]。
三、双指针法:高效生成有序数组(推荐)
核心思想:利用原数组两端元素平方后的最大值特性,使用双指针从两端向中间遍历,依次填充新数组的最大值。
双指针定义:
- 左指针
i:指向原数组的起始位置(最小元素)。 - 右指针
j:指向原数组的末尾位置(最大元素)。 - 结果数组指针
k:指向结果数组的末尾位置(用于填充最大值)。
步骤:
- 初始化指针:
i = 0,j = 数组长度-1,k = 数组长度-1。 - 比较平方值:比较
nums[i]²和nums[j]²的大小:- 若
nums[i]² < nums[j]²:将nums[j]²放入结果数组的k位置,j左移一位,k左移一位。 - 否则:将
nums[i]²放入结果数组的k位置,i右移一位,k左移一位。
- 若
- 循环条件:重复步骤 2,直到
i > j(所有元素处理完毕)。
四. 代码示例
class Solution {public int[] sortedSquares(int[] nums) {int right = nums.length - 1;int left = 0;int[] result = new int[nums.length];int index = result.length - 1;while (left <= right) {if (nums[left] * nums[left] > nums[right] * nums[right]) {// 正数的相对位置是不变的, 需要调整的是负数平方后的相对位置result[index--] = nums[left] * nums[left];++left;} else {result[index--] = nums[right] * nums[right];--right;}}return result;}
}209. 长度最小的子数组
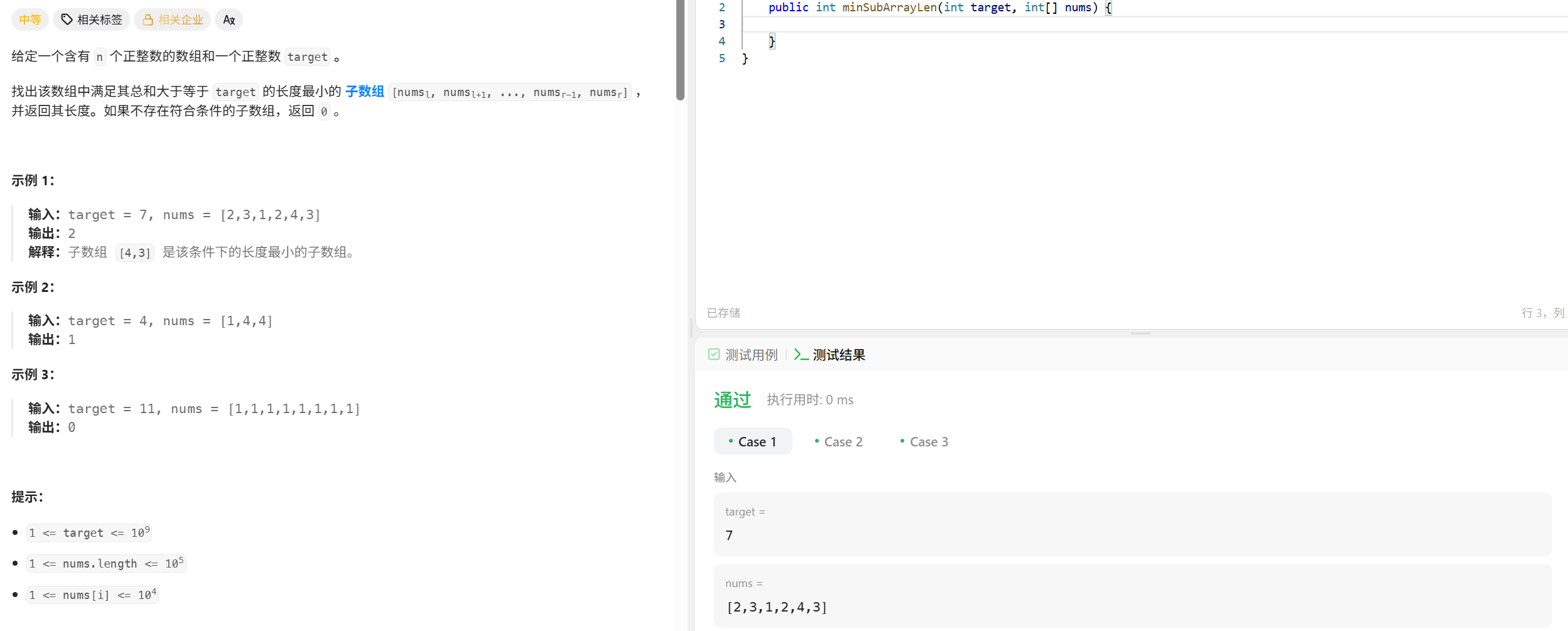
一、核心逻辑:滑动窗口找最小长度
由于数组元素均为正整数(根据题目隐含条件,若存在负数需额外处理,但该解法默认元素为正),当子数组和大于等于目标值时,缩短窗口左侧可尝试找到更短的有效子数组。因此,可通过滑动窗口(双指针)动态调整子数组范围,高效计算满足条件的最小长度。
二、滑动窗口解法:双指针动态调整
思路:使用快指针扩展窗口右边界,累计子数组和;当和大于等于目标值时,移动慢指针收缩左边界,更新最小长度,同时减少累计和。
双指针定义:
- 慢指针
slow:指向当前子数组的起始位置,用于收缩窗口。 - 快指针
fast:指向当前子数组的结束位置,用于扩展窗口。 - 辅助变量
sum:记录当前窗口(子数组)的元素和;len:记录满足条件的子数组最小长度(初始化为最大值)。
步骤:
- 初始化指针与变量:
slow = 0,sum = 0,len = Integer.MAX_VALUE。 - 扩展窗口:快指针
fast从 0 开始遍历数组,每次将nums[fast]加入sum。 - 收缩窗口:当
sum >= target时,执行以下操作:- 计算当前窗口长度(
fast - slow + 1),与len比较并更新最小值。 - 将
nums[slow]从sum中减去,慢指针slow右移一位,缩小窗口范围。 - 重复收缩操作,直到
sum < target为止。
- 计算当前窗口长度(
- 结果处理:遍历结束后,若
len仍为初始最大值(无满足条件的子数组),返回 0;否则返回len。
public int minSubArrayLen(int target, int[] nums) {int len = Integer.MAX_VALUE;int slow = 0;int fast;int sum = 0;for (fast = 0; fast < nums.length; fast++) {sum += nums[fast];while (sum >= target) {sum -= nums[slow];len = Math.min(fast - slow + 1, len);slow++;}}return len == Integer.MAX_VALUE ? 0 : len;}至此,大功告成!🎉🎉🎉
