当前位置：首页 > news >正文

BitDistiller：通过自蒸馏释放 Sub-4-Bit 大语言模型的潜力

news 2025/7/25 8:42:53

温馨提示：
本篇文章已同步至"AI专题精讲" BitDistiller：通过自蒸馏释放 Sub-4-Bit 大语言模型的潜力

摘要

大语言模型（LLMs）的规模不断扩大，在自然语言处理方面取得了令人瞩目的进展，但这也带来了显著的部署挑战。权重量化已成为广泛采用的解决方案，用于降低内存和计算需求。本文提出了 BitDistiller，一个融合了量化感知训练（Quantization-Aware Training, QAT）与知识蒸馏（Knowledge Distillation, KD）的框架，用以提升超低精度（sub-4-bit）LLMs 的性能。具体而言，BitDistiller 首先引入了一个定制的非对称量化与裁剪技术，以最大程度地保留量化权重的精度；随后提出了一种新颖的置信感知 Kullback-Leibler 散度（Confidence-Aware Kullback-Leibler Divergence, CAKLD）目标函数，并以自蒸馏的方式应用于训练过程中，从而实现更快的收敛速度和更优的模型性能。实验结果表明，BitDistiller 在3-bit和2-bit配置下，在通用语言理解和复杂推理任务中均显著优于现有方法。值得注意的是，BitDistiller 在资源效率方面也更具优势，所需的数据和训练资源更少。代码开源于：https://github.com/DD-DuDa/BitDistiller。

1 引言

扩大模型规模是大语言模型（LLMs）取得成功的关键因素，使其在多种自然语言处理任务中展现出前所未有的性能（Brown et al., 2020；Touvron et al., 2023；Kaplan et al., 2020）。然而，模型规模的不断增长也带来了部署方面的重大挑战，尤其是在资源受限的设备上，由于模型的内存占用和计算需求极为庞大。

权重量化作为一种提高 LLM 效率和可部署性的常用策略，能够在尽量不牺牲性能的前提下大幅压缩模型体积（Gholami et al., 2022）。在实际应用中，4-bit 量化因其在压缩比与性能保留之间的良好平衡，被广泛采用（Lin et al., 2023；Frantar et al., 2022；Liu et al., 2023a）。
在这里插入图片描述

然而，sub-4-bit 量化会显著降低模型权重的保真度，进而导致模型性能下降，尤其是在小模型或需要复杂推理的任务中更为明显（Dettmers 和 Zettlemoyer，2023）。为应对这一问题，研究者提出了多种后训练量化（Post-Training Quantization, PTQ）和量化感知训练（Quantization-Aware Training, QAT）方法（Chee 等，2023；Shao 等，2023）。PTQ 的优势在于无需重新训练模型，但在极低比特精度下很难维持模型性能。相比之下，QAT 将量化过程融入训练环节，使模型能动态适应精度降低，从而更好地保留精度（Liu 等，2023b；Kim 等，2023a）。尽管早期成果令人鼓舞，但要在极低比特的 QAT 场景中实现优异的模型性能，仍需解决两个核心难题：如何在量化中最大限度保留权重精度，以及如何在训练中有效学习低比特表示。

在本文中，我们提出了 BitDistiller —— 一个将 QAT 与知识蒸馏（Knowledge Distillation, KD）有机融合的新型框架，旨在显著提升 sub-4-bit 量化 LLM 的性能。为尽量减少量化误差，BitDistiller 采用了定制的非对称量化与裁剪策略，以尽可能保留全精度模型的能力，尤其是在超低比特设定下。为了有效且高效地学习低比特表示，BitDistiller 采用了一种简洁而高效的自蒸馏机制，即使用全精度模型作为教师模型，引导低比特学生模型的训练。值得一提的是，BitDistiller 创新性地引入了置信感知 Kullback-Leibler 散度（Confidence-Aware Kullback-Leibler Divergence, CAKLD）**作为目标函数，从而优化知识迁移效果，实现更快的收敛速度与更佳的模型性能。

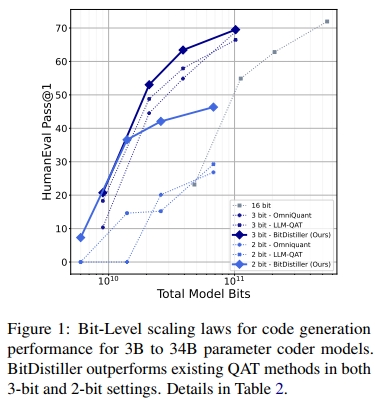
我们在涵盖通用语言理解、数学推理与代码生成等多种任务的基准上进行了实证评估，结果表明 BitDistiller 在 sub-4-bit 量化领域显著优于现有的 PTQ 与 QAT 方法。如图 1 所示，BitDistiller 在代码推理基准上，于 3-bit 与 2-bit 配置下均取得了最优的扩展性能表现（scaling law）。此外，BitDistiller 在资源效率方面也表现突出，对训练数据与资源的需求更低，标志着在资源受限设备上部署强大 LLMs 迈出了重要一步。

2 背景与相关工作

2.1 面向 LLM 的权重量化

PTQ 与 QAT
后训练量化（Post-Training Quantization, PTQ）直接应用于预训练模型，无需额外训练。LLM 的 PTQ 方法通常依赖于误差调整策略（Frantar 等，2022；Chee 等，2023）或优先保留关键权重（Dettmers 等，2023b；Lin 等，2023；Kim 等，2023b）。然而，由于缺乏重新训练过程，PTQ 在极低比特精度下容易导致模型性能大幅下降。相比之下，量化感知训练（Quantization-Aware Training, QAT）将量化过程整合到训练阶段，使模型能学习更适用于低比特权重的表示方式。已有的 QAT 方法如 LLM-QAT（Liu 等，2023b）、OmniQuant（Shao 等，2023）、PB-LLM（Shang 等，2023）和 BitNet（Wang 等，2023）在提升模型性能方面已取得显著成效。尽管如此，QAT 依然面临对大量训练数据与资源的高度依赖，仍有较大优化空间。在本研究中，我们结合 QAT 与知识蒸馏（Knowledge Distillation, KD），以增强在 sub-4-bit 场景下量化 LLM 的性能。

量化粒度与格式优化
大量研究表明，采用更细粒度的量化策略（如分组量化）相比于逐层（layer-wise）或通道级（channel-wise）量化方法能获得更高精度（Shen 等，2020；Frantar 等，2022）。此外，在 LLM 的量化中，浮点数格式（如 FP8、FP4、NF4）被证明比整数格式（如 INT8、INT4）具有更好的精度表现（Kuzmin 等，2022；Dettmers 和 Zettlemoyer，2023；Zhang 等，2023b）。尤其值得注意的是，非对称量化（asymmetric quantization）在浮点格式中优于对称量化，因为它能更好地适应模型权重的分布特性（Zhang 等，2023a）。BitDistiller 遵循这些经验，采用更细粒度的分组方式与非对称量化策略来提升性能。

2.2 面向 LLM 的知识蒸馏

在大语言模型领域，白盒知识蒸馏（white-box KD）因教师模型的可访问性而愈发流行，这种方式可以更有效地将教师模型的知识表示传递给学生模型（Hinton 等，2015；Zhu 等，2023）。例如，MINILLM（Gu 等，2023）使用反向 KL 散度（KLD）来保证语言生成的准确性与保真性。GKD（Agarwal 等，2023）则探索了更广义的 Jensen-Shannon 散度（JSD），并通过从学生模型中采样输出缓解分布失配的问题。

为了实现极高的压缩比，将 KD 与模型量化相结合是一种有前景的策略，KD 能有效缓解量化后模型的精度损失（Zhang 等，2020；Kim 等，2022）。在应用 QAT 与 KD 结合的前沿研究中，TSLD（Kim 等，2023a）考虑了过拟合风险，并结合了 logit 蒸馏与真实标签损失；LLM-QAT 则利用教师模型生成的随机数据进行无数据蒸馏（data-free distillation）。与 TSLD 和 LLM-QAT 不同，我们的方法在极低比特量化精度下实现了更优的性能表现与更高的资源效率。

3 方法

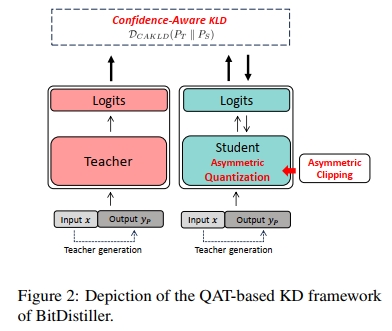
在这里插入图片描述

在本节中，我们介绍 BitDistiller ——一个面向大语言模型（LLMs）的量化感知训练（QAT）与自蒸馏框架，如图 2 所示。为了在量化过程中最大程度地保留权重的保真性，我们首先提出一种非对称量化与截断方法（见第 3.1 节）。其次，为了抵消因精度降低而带来的性能下降，我们引入知识蒸馏（Knowledge Distillation），并提出一种新的置信度感知 KL 散度（Confidence-Aware KL Divergence，CAKLD）作为目标函数，在该目标中，全精度模型作为教师模型，而低精度模型则作为学生模型（见第 3.2 节）。

算法 1 概述了 BitDistiller 的整体流程。给定全精度权重 ww，BitDistiller 首先对 ww 应用非对称截断操作，以缓解异常值的影响（第 1 行），该步骤在训练循环之前进行。随后，在每一个训练步骤中，BitDistiller 使用量化后的权重 wQtw_{Qt} 进行前向传播（forward），并通过所提出的 CAKLD 损失函数 计算损失值（第 4-5 行），然后更新全精度权重（第 6-7 行）（Bengio 等人，2013）。当训练结束后，BitDistiller 输出最终的量化权重。

3.1 非对称量化与截断

在大语言模型（LLMs）的权重量化中，采用更细粒度（即更小的分组规模）通常会导致权重分组呈现非对称分布，并且伴随离群值的出现。在低比特的后训练量化（PTQ）场景中，若要维持模型性能，恰当处理这种非对称性是至关重要的。

我们的研究发现：在极低比特的量化感知训练（QAT）中（如 3 比特和 2 比特配置），非对称性带来的影响更为显著，因此需要定制的策略加以应对。

因此，在 BitDistiller 中，我们引入了非对称量化技术，并结合非对称截断策略，以提升量化权重的表达保真度，最大限度地保留全精度模型的能力。
在这里插入图片描述
非对称量化
已有研究表明，在 LLM 量化中，浮点格式（如 FP、NF）通常优于整数格式（INT）（Dettmers 等，2023a；Liu 等，2023a）。然而，当量化精度降低至 2-bit 时，我们观察到 FP/NF 格式的效果明显下降。FP/NF 格式之所以在高比特位中表现良好，是由于其非均匀分布特性，能够捕捉更广泛的数值范围，这种非均匀分布与 LLM 中权重张量的自然分布更加契合。

但在 2-bit 场景中，由于其仅能表示四个离散值，表示能力受限，导致非均匀分布的优势无法有效发挥，从而阻碍了每个数值的有效利用。基于以上观察，我们在 2-bit 以上的量化中采用 NF 格式，而在 2-bit 场景下则改用 INT 格式。

对于 NF 格式（如 NF3），我们采用 AFPQ 方法（Zhang 等，2023a）实现非对称量化：为正权重 $w\_{pos}$ 和负权重 $w\_{neg}$ 分别设定独立的缩放因子 $s\_{pos}$ 与 $s\_{neg}$ ，如公式 (1) 所示。
对于 INT 格式（如 INT2），我们则采用传统的非对称方法：使用一个单一的缩放因子和一个指定的零点（zero point），如公式 (2) 所示。

$\left\{ \begin{array} { l l } { { \lfloor { \frac { w _ { p o s } } { s _ { p o s } } } \rceil } , } & { { \mathrm { i f ~ } } w > 0 } \\ { { \lfloor { \frac { w _ { n e g } } { s _ { n e g } } } \rceil } , } & { { \mathrm { i f ~ } } w \leq 0 } \end{array} \right. }\quad(1)$

$\cdot } A s y m : Q ( w ) = \lfloor \frac { w - z } { s } \rceil\quad(2)$

非对称剪枝（Asymmetric Clipping）
剪枝（clipping）是一种通过限制权重数值范围来提高量化后模型精度的策略，已有研究证实了其在保持量化精度方面的重要作用（Sakr 等，2022；Shao 等，2023）。然而，朴素的剪枝方法通常效果有限，而更先进的剪枝技术又存在高计算成本的问题，不适用于实际的 QAT 训练过程（Li 等，2019；Jung 等，2019）。

为克服这一难题，我们提出仅在 QAT 初始化阶段使用非对称剪枝策略。在训练开始之前进行非对称剪枝，能够为模型提供良好的初始点，在不引入迭代剪枝优化的高昂成本的前提下，显著提升最终量化模型的精度。

具体而言，为了在 QAT 初始化中实现非对称剪枝，我们利用从一小部分校准数据中缓存得到的输入特征 $X$ ，为模型的每一层自动搜索两个最优的剪枝阈值 $α\alpha$ 和 $β\beta$ 。这两个值的目标是最小化量化前后的输出差异。形式上，我们优化以下目标函数：
$α∗,β∗=argmin⁡α,β∣∣Q(wc)X−wX∣∣\alpha ^ { * } , \beta ^ { * } = \operatorname * { a r g m i n } _ { \alpha , \beta } \lvert \lvert Q ( w _ { c } ) X - w X \rvert \rvert$

$wc=Clip(w,α,β){α∈[min_val,0)β∈(0,max_val](3)w_c = \text{Clip}(w, \alpha, \beta) \begin{cases} \alpha \in [\text{min\_val}, 0) \\ \beta \in (0, \text{max\_val}] \end{cases}\quad(3)$

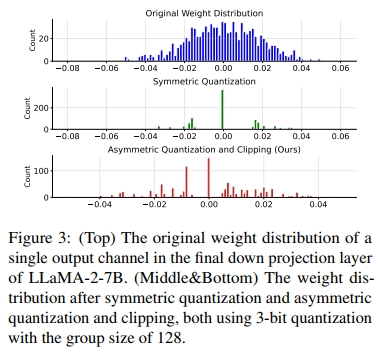
为了展示非对称量化和裁剪的有效性，我们进行了张量级别的分析。我们从 LLaMa-2-7B 模型中随机选取了一个权重张量，重点关注其中的一个输出通道。如图 3 所示，我们采用的非对称量化和裁剪方法相比对称量化能够更好地保持高保真度。关于非对称量化和裁剪对模型性能影响的更详细消融研究，见第 4.4 节的表 3。

在这里插入图片描述

3.2 带有 CAKLD 的自我蒸馏

为更好地抵消精度降低带来的性能下降，我们提出在量化感知训练（QAT）中采用知识蒸馏（KD），其中全精度模型作为教师，量化后的模型作为学生：

$D(P_T \parallel P_S)\quad(4)$

式中， $D$ 表示两个分布之间的散度度量， $P_T$ 和 $P_S$ 分别代表全精度模型和量化模型。

知识蒸馏（KD）的直觉可以从两个方面理解。首先，学习 token 级别的概率分布有助于量化模型更好地模仿其全精度对应模型（Hinton 等，2015），从而重新获得强大的下游任务性能。其次，鉴于大型语言模型（LLM）的生成特性，利用全精度模型来扩展用于量化感知训练（QAT）的数据规模变得十分容易。

用于蒸馏的散度度量 $D$ 选择至关重要。Agarwal 等（2023）发现，反向 KL 散度（即 $D_{KL}(P_S \| P_T)$ ）所倡导的“模式寻求”行为在指令调优（Chung 等，2022）任务中表现优于正向 KL 散度（即 $D_{KL}(P_T \| P_S)$ ），而正向 KL 散度促进“模式覆盖”，在摘要等通用文本生成任务（Narayan 等，2018）中表现更好。为了给 QAT 提供一种通用方案，我们旨在自动权衡“模式寻求”与“模式覆盖”的行为，而不是基于对下游任务的经验理解手动选择。
在这里插入图片描述
为此，我们提出了一种新颖的置信感知 KL 散度，简称 CAKLD。它通过一个由平均 token 概率估计的系数 $γ$ ，将反向 KL 和正向 KL 混合起来，从而使得“模式寻求”和“模式覆盖”的行为能够根据全精度模型对训练数据的置信度自动权衡：
$DCAKLD(PT∥PS)=γDKL(PS∥PT)+(1−γ)DKL(PT∥PS)D_{\text{CAKLD}}(P_T \parallel P_S) = \gamma D_{KL}(P_S \parallel P_T) + (1 - \gamma) D_{KL}(P_T \parallel P_S)$

$DKL(PT∥PS)=E(x,y)∼D[1∣y∣∑i=1∣y∣Ec∼PT(⋅∣x,y<i)[log⁡PT(c∣x,y<i)PS(c∣x,y<i)]](5)D_{KL}(P_T \parallel P_S) = \mathbb{E}_{(x,y) \sim D} \left[ \frac{1}{|y|} \sum_{i=1}^{|y|} \mathbb{E}_{c \sim P_T(\cdot | x, y_{<i})} \left[ \log \frac{P_T(c | x, y_{<i})}{P_S(c | x, y_{<i})} \right] \right]\quad(5)$

$γ=E(x,y)∼D[1∣y∣∑i=1∣y∣PT(yi∣x,y<i)]\gamma = \mathbb{E}_{(x,y) \sim D} \left[ \frac{1}{|y|} \sum_{i=1}^{|y|} P_T(y_i | x, y_{<i}) \right]$

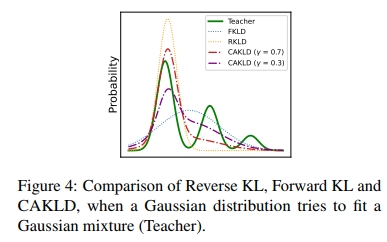
直观来看，当全精度模型对训练数据较为自信时，CAKLD 会更倾向于“模式寻求”的行为；反之，当全精度模型对数据不确定时，CAKLD 会更倾向于“模式覆盖”的行为，因为仅仅建模单一模式并非最优。图 4 展示了在高斯分布拟合高斯混合分布时，反向 KL 散度、正向 KL 散度与 CAKLD 之间的差异。显然，CAKLD 能够通过系数有效权衡“模式寻求”和“模式覆盖”的行为。有关详细的性能对比和深入分析，请参见图 6 及附录 A.2。

温馨提示：
阅读全文请访问"AI深语解构" BitDistiller：通过自蒸馏释放 Sub-4-Bit 大语言模型的潜力

查看全文

http://www.lryc.cn/news/596897.html