当前位置：首页 > news >正文

BiLLM：突破大语言模型后训练量化的极限

news 2025/7/25 11:56:36

温馨提示：
本篇文章已同步至"AI专题精讲" BiLLM：突破大语言模型后训练量化的极限

摘要

预训练的大语言模型（LLMs）展现出卓越的通用语言处理能力，但同时对内存和计算资源提出了极高要求。作为一种强大的压缩技术，二值化（binarization）可以将模型权重极大压缩至仅1位，从而显著降低计算和内存开销。然而，现有的量化技术在超低比特宽度下难以保持LLM的性能。为应对这一挑战，我们提出了 BiLLM，一种面向预训练LLM的开创性1比特后训练量化（post-training quantization）方法。

BiLLM 基于 LLM 权重的分布特性，首先识别并结构性地选择重要权重，并通过一种有效的二值残差逼近（binary residual approximation）策略最小化压缩误差。此外，考虑到非重要权重呈钟形分布，我们提出了一种 最优分割搜索（optimal splitting search）方法，以实现更精确的分组与二值化。

BiLLM 首次在多种 LLM 家族和评测指标上实现了高精度的推理效果（例如在 LLaMA2-70B 上实现 8.41 的 perplexity），在精度上显著优于现有最先进的量化方法。同时，BiLLM 能够在单张 GPU 上于 0.5 小时内完成一个 70 亿参数模型的二值化，展现出良好的时间效率。我们的代码开源于：
https://github.com/Aaronhuang-778/BiLLM

1. 引言

近年来，基于 transformer（Vaswani et al., 2017）的大语言模型（LLMs）在自然语言处理领域引发了广泛关注。诸如 OPT（Zhang et al., 2022）和 LLaMA（Touvron et al., 2023a）等预训练 LLM 在多项评测基准上表现优异。然而，LLMs 由于其庞大的参数规模和计算需求，在内存受限设备上的部署面临极大挑战。例如，广泛使用的 LLaMA2-70B（Touvron et al., 2023b）模型拥有 700 亿参数，在半精度（FP16）格式下需要 150 GB 的存储空间。这意味着其推理过程至少需要两张各配备 80 GB 显存的 A100 GPU 才能运行。
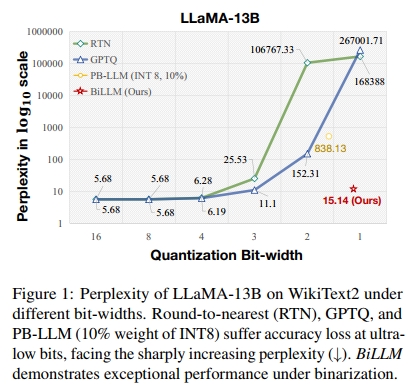
在这里插入图片描述
模型量化作为一种压缩神经网络的高效技术，已经广泛应用于减少大语言模型（LLMs）的模型体积，并显著节省 GPU 内存开销（Dettmers et al., 2022）。当前的量化技术主要分为两类：量化感知训练（Quantization-Aware Training, QAT）与后训练量化（Post-Training Quantization, PTQ）。QAT 在量化过程中需要进行微调和再训练，而 PTQ 则通过省略反向传播极大简化了计算流程，从而加快量化速度，并提升了其实用性（Frantar et al., 2022; Shang et al., 2023; Lin et al., 2023）。考虑到 LLM 结构深、参数量大，在时间和资源受限的情境下，PTQ 由于其快速量化的特性而展现出显著优势（Zhu et al., 2023）。

尽管已有 PTQ 方法在 8-bit 与 4-bit 量化方面取得了一定成功（Dettmers et al., 2022; 2023b; Frantar et al., 2022; Xiao et al., 2023; Frantar & Alistarh, 2022），但 LLM 的规模不断扩大，促使我们必须追求更激进的量化策略（Shang et al., 2023）。神经网络二值化（binarization） 是一种有前景的技术，其将权重位宽压缩至仅 1 位（Helwegen et al., 2019; Qin et al., 2020; 2023）。然而，正如图 1 所示，当前先进的 LLM PTQ 方法在超低比特（≤3 bit）下会出现性能崩塌现象。造成这一现象的根本原因在于：量化后的权重与原始权重之间存在显著差异。即使是最新提出的针对 LLM 的二值 PTQ 方法 PB-LLM（Shang et al., 2023），其在权重平均仅为 1.7 bit 的情况下，perplexity 仍维持在 800 左右。这一现象凸显出当前 PTQ 方法在实现 LLM 权重量化二值化方面面临的挑战。

为应对这一问题，我们对预训练 LLM 的权重分布进行了实证分析，研究结果详见附录 G，揭示了两个关键观察结果：

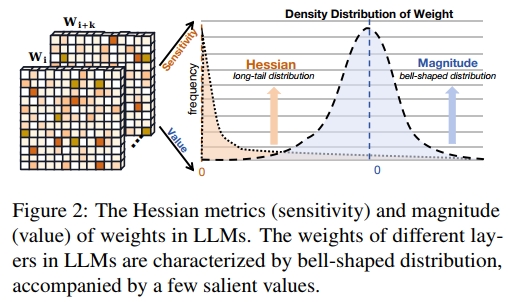
LLM 权重的二阶 Hessian 矩阵表现出极端长尾分布，而 Hessian 通常被用来衡量神经网络中权重元素的重要性（LeCun et al., 1989; Dong et al., 2019）。如图 2 所示，只有少部分权重具有显著高的 Hessian 值，对层输出有着关键影响；而大部分 Hessian 值则集中在接近 0 附近。
LLM 权重幅值的密度分布呈现出钟形结构。该分布与高斯分布或拉普拉斯分布在特性上非常相似（Blundell et al., 2015）。图 2 显示，大部分权重值集中在 0 附近，呈现非均匀的钟形分布。

上述发现意味着：a）LLM 中只有少数权重起到关键作用，而大多数权重呈现出冗余特性（Shang et al., 2023; Dettmers et al., 2023b）；b）在钟形分布下进行最激进的位宽压缩（二值化）时，将带来最严重的量化误差（Jacob et al., 2018）。

受到上述启发，我们提出了一种面向 LLM 的新型 1-bit PTQ 框架 —— BiLLM，包含两项核心设计以实现高精度的权重量化二值化：

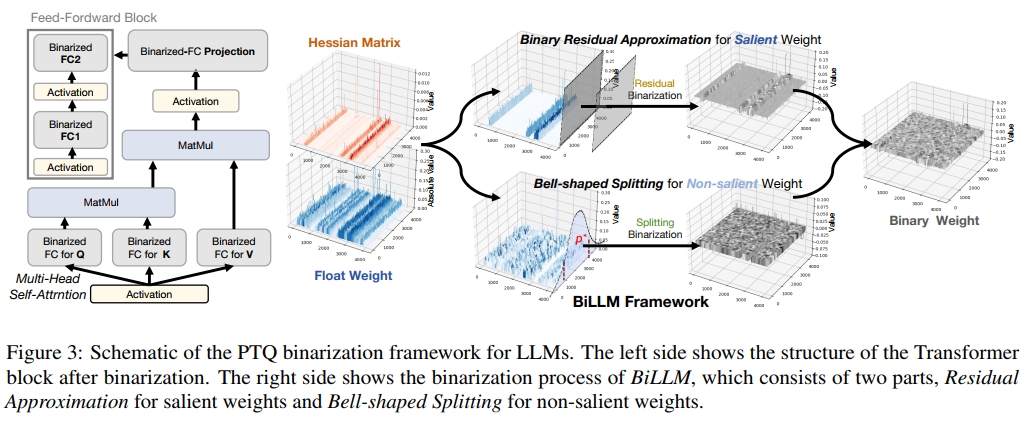
首先，基于 Hessian 指标，我们对重要权重进行结构化选择（见图 3 右上），以在精度和存储节省之间实现权衡；并针对这些动态范围较大的权重开发残差逼近策略，最大程度恢复其信息。

其次，针对剩余的非重要权重（图 3 右下），我们设计了一种 最优分割二值化策略（optimal splitting binarization strategy），通过精细的搜索过程确定权重分布的最优断点，并分别对各分段进行二值化，以最小化量化误差。

此外，BiLLM 默认集成了基于 block 的误差补偿机制，遵循已有主流做法（Frantar et al., 2022; Shang et al., 2023），进一步降低量化误差。
在这里插入图片描述
大量实验证明，BiLLM 在多个 LLM 系列和多种评估指标上均达到了当前最先进（SOTA）的性能，并首次在后训练量化（PTQ）中实现了平均仅 1.07∼1.11 bit 的极致紧凑位宽。例如，在 Wikitext2（Merity et al., 2016）评测中，BiLLM 在 LLaMA-65B（Touvron et al., 2023a）和 LLaMA2-70B（Touvron et al., 2023b）上分别以仅 1.08-bit 权重达成了 8.49 和 8.41 的 perplexity，甚至优于使用 FP16 权重的 OPT-66B（Zhang et al., 2022）所达到的 9.34 的表现。

2. 相关工作

2.1. 大语言模型量化

量化是将高精度参数映射到离散范围的过程。这种方法在不改变模型结构的前提下压缩参数，有效降低了深度神经网络的存储和计算开销。近年来的研究已经成功地将 QAT（Quantization-Aware Training，量化感知训练）和 PTQ（Post-Training Quantization，后训练量化）应用于大语言模型（LLMs）。

QAT 通过量化感知的再训练策略，可以更好地保持量化模型的性能。例如，LLMQAT（Liu et al., 2023）通过无数据蒸馏的方法解决了 QAT 中的数据障碍问题。然而，对于参数规模极大的 LLM 来说，再训练的成本非常高且效率低下。因此，一些方法如 QLoRA（Dettmers et al., 2023a）转而关注参数高效微调（PEFT）策略，用于对 LLM 进行量化，以提升 QAT 的效率。尽管如此，即使是这些高效的微调量化策略，也需要超过 24 小时的 GPU 时间。
在这里插入图片描述
因此，PTQ 策略已成为高效量化 LLM 的重要选择。诸如 BRECQ（Li et al., 2021）、ZeroQuant（Yao et al.）以及 LLM.int8()（Dettmers et al., 2022）等工作通过为自定义量化块添加额外的分组标签来提升量化精度。其他研究则采用特征分段策略，例如 PB-LLM（Shang et al., 2023）和 SpQR（Dettmers et al., 2023b），它们保留了离群特征或量化误差较大的部分的比特宽度为 FP16 或 INT8，从而缓解了量化带来的精度损失。

GPTQ（Frantar et al., 2022）则采用更为精确的量化框架，通过基于 Hessian 的二阶误差补偿（Frantar & Alistarh, 2022）来减少 LLM 的块量化误差，在低比特（4 位）量化中实现了令人满意的性能。SmoothQuant（Xiao et al., 2023）引入了对权重和激活异常值进行缩放的策略，以简化量化过程。随后，AWQ（Lin et al., 2023）和 OWQ（Lee et al., 2023）也提出了对关键权重通道进行尺度变换的策略，以增强其激活特征的信息表达能力。

2.2 网络二值化

二值化压缩技术可以将参数量化为仅 1 比特，表示为 ±1。在前向传播过程中，使用符号函数对原始参数张量进行二值化：

$Wb=α⋅sign(Wf),(1)\mathbf{W}_b = \alpha \cdot \mathrm{sign}(\mathbf{W}_f), \quad(1)$

$sign(x)={1ifx≥0,−1otherwise.(2)\mathrm{sign}(x) = \left\{ \begin{array}{ll} 1 & \mathrm{if}~x \geq 0, \\ -1 & \mathrm{otherwise}. \end{array} \right. \quad(2)$

其中， $Wf∈Rn×m\mathbf{W}_f \in \mathbb{R}^{n \times m}$ 表示全精度权重， $Wb∈Rn×m\mathbf{W}_b \in \mathbb{R}^{n \times m}$ 为二值化后的输出，n 和 m 表示权重矩阵的维度大小。 $α$ 表示缩放因子（Courbariaux et al., 2016）。二值化通常采用通道级别的缩放方式（Rastegari et al., 2016；Qin et al., 2023），因此 $α \in R^{n}$ 。

大多数早期的二值化工作采用基于 QAT 的量化框架（Qin 等，2023）。为了解决由 sign(·) 函数引起的梯度消失问题，通常采用直通估计器（STE，Bengio 等，2013）。Binary Weight Network（BWN，Rastegari 等，2016）最初被提出用于通过对权重进行二值化、同时保留全精度激活值的方式来执行神经网络计算，而 XNOR-Net（Rastegari 等，2016）则在此基础上进一步将激活值也进行二值化。这两种方法都通过对缩放因子 α 的动态搜索来最小化量化误差。DoReFa-Net（Zhou 等，2016）进一步扩展了 XNOR-Net 的方法，通过对梯度进行量化来加速网络训练。在二值化任务中也引入了组分段思想，例如 Syq（Faraone 等，2018）利用网络权重对组的规模进行划分，以降低二值化误差。

鉴于二值化技术在 Transformer（Wang 等，2023）和 BERT（Qin 等，2022）上的成功应用，我们认为将其应用于 LLMs 具有广阔的潜力。PB-LLM（Shang 等，2023）探索了二值化 QAT 和 PTQ 策略对 LLM 的影响，但它必须保留大量（超过 30%）的权重为 8 位，才能使 LLM 生成合理的输出。由于存在大量 INT8 权重，该方法仍具有相对较高的平均比特宽度。为了解决这一问题，我们提出了 BiLLM，旨在突破 LLM 的 PTQ 二值化极限。

3 方法

为了实现对 LLM 的精确二值化，我们的方法是针对“显著权重（salient weights）”和“非显著权重（non-salient weights）”分别设计不同的二值化策略。我们首先在第 3.1 节介绍显著权重的选择规则及其二值化策略；然后在第 3.2 节中，详细阐述面向非显著权重的基于分布的二值化方法。

3.1 LLM 的显著权重二值化

在深度神经网络中，并非所有参数都具有相同的重要性。仅使用权重的数值大小无法完全衡量每个元素对模型性能的影响。Hessian 指标是一种常见的参数敏感性检测标准（Dong 等，2019；Dettmers 等，2023b；2022）。因此，我们利用 Hessian 矩阵来评估每一层待二值化参数的重要性。我们实现了一种优化的计算流程，以获取权重敏感性，从而在不牺牲效率的前提下得到参数的重要性度量：
$\frac { w _ { i } ^ { 2 } } { [ \mathbf { H } ^ { - 1 } ] _ { i i } ^ { 2 } }\quad(3)$
其中， $H$ 表示每一层的 Hessian 矩阵， $w_i$ 表示每个权重元素的原始数值。在后续内容中， $s_i$ 作为评估权重元素显著性的指标，并被用作结构化选择的特征标记。

结构化搜索选择

使用非结构化选择（unstructured selection）可以覆盖所有显著元素，但这需要额外实现一个 1 位的位图索引（bitmap index）（Chan & Ioannidis, 1998），导致平均比特宽度增加。这种权衡效率较低，尤其是对于仅占总量 1%~5% 的 Hessian 异常权重（outlier weights）（Yao 等，2023）。

通过对 LLM 中敏感度分布的分析，我们发现大部分敏感的 Hessian 权重值主要集中在特定的列或行（详见附录 G）。这种现象归因于多头自注意力机制的收敛效应，因此促使我们采用结构化的策略选择显著权重，以减少额外的位图开销。由于 BiLLM 采用每通道（或每行）类型的二值化，我们通过对整个权重矩阵按列进行分段来确定显著性。

我们将列显著性按降序排列，并引入一种优化的搜索算法，旨在最小化量化误差，从而确定显著组中列的数量。为阐明该方法，首先基于公式（1）定义二值化量化的目标：
$arg⁡min⁡α,B∥W−αB∥2(4)\arg \operatorname* { m i n } _ { \alpha , \mathbf { B } } \| \mathbf { W } - \alpha \mathbf { B } \| ^ { 2 }\quad(4)$
其中， $\in \{-1, +1\}^{n \times k}$ ， $k$ 是选中列的数量。根据 Rastegari 等人（2016）的方法，最优的缩放因子 $α\alpha$ 和二值矩阵 $B$ 可简单地通过以下方式求解：

$α=∥W∥ℓ1n×k,B=sign(W)\alpha = \frac{\|W\|_{\ell_1}}{n \times k}, \quad B = \mathrm{sign}(W)$

然后，选取显著列的优化目标函数定义为：

$arg⁡min⁡Wuns∥W−(αsal⋅sign(Wsal)∪αuns⋅sign(Wuns))∥2(5)\arg \min_{W_{uns}} \left\| W - \left( \alpha_{sal} \cdot \mathrm{sign}(W_{sal}) \cup \alpha_{uns} \cdot \mathrm{sign}(W_{uns}) \right) \right\|^2\quad(5)$

其中， $W_{sal}$ 表示原始权重中被选择的显著列的组合， $W_{uns}$ 是剩余的非显著部分。显然，

$W_{sal} \cup W_{uns}$

因此，唯一的可调参数是显著部分 $W_{sal}$ 中列的数量（即 $k$ ）。通过调整这个参数，可以平衡二值化误差和压缩率。
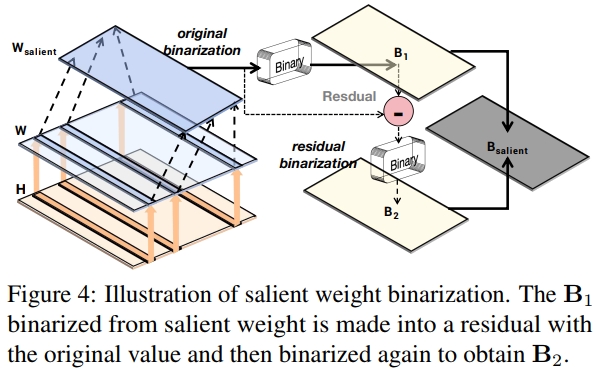
在这里插入图片描述

二值残差近似。显著权重数量有限，但在聚合时呈现显著的方差。若直接用 INT8 或 FP16 格式保存这些权重，会导致平均权重位宽增加，从而削弱二值化带来的压缩优势。传统对显著权重的二值化方法往往产生较大的量化误差。为此，我们提出了一种针对显著权重的残差近似二值化方法。

与对整个权重矩阵进行高阶量化（Li 等，2017）不同，我们的方法仅对选定的显著权重子集进行二阶近似，以最小化二值化误差。这一策略既保证了显著权重的精度，又减少了位宽开销。如图 4 所示，该方法通过递归计算的策略实现权重二值化的补偿，对初次二值化后的残差再次进行二值化。

基于公式（4），我们为显著权重提出了重新设计的残差近似优化，定义如下：

${αo∗,Bo∗=arg⁡min⁡αo,Bo∥W−αoBo∥2,αr∗,Br∗=arg⁡min⁡αr,Br∥(W−αo∗Bo∗)−αrBr∥2(6)\begin{cases} \alpha_o^*, B_o^* = \arg \min_{\alpha_o, B_o} \| W - \alpha_o B_o \|^2, \\ \alpha_r^*, B_r^* = \arg \min_{\alpha_r, B_r} \| (W - \alpha_o^* B_o^*) - \alpha_r B_r \|^2 \end{cases}\quad(6)$

其中， $B_o$ 表示初始的二值张量， $B_r$ 是与 $B_o$ 同尺寸的残差二值化矩阵。我们采用与公式（4）中相同的求解方法，高效地求解这两个二值化优化目标。

在这里插入图片描述

最终，我们得到如下的近似表达式：

$W≈αo∗Bo∗+αr∗Br∗.(7)\mathbf{W} \approx \alpha_{o}^* \mathbf{B}_{o}^* + \alpha_{r}^* \mathbf{B}_{r}^* . \tag{7}$

可以轻易证明，公式（7）中的残差方法比公式（4）中的直接二值化方法具有更低的量化误差。我们定义残差二值化误差为：

$Erb=∥W−αo∗Bo∗−αr∗Br∗∥2.(8)\mathbf{\mathcal{E}}_{rb} = \| \mathbf{W} - \alpha_{o}^* \mathbf{B}_{o}^* - \alpha_{r}^* \mathbf{B}_{r}^* \|^2 . \tag{8}$

根据公式（4），原始的二值化量化误差计算为

$∥W−αo∗Bo∗∥2,\| \mathbf{W} - \alpha_{o}^* \mathbf{B}_{o}^* \|^2 ,$

而根据公式（6）的第二个子式，我们可以得到不等式

$Erb≤∥W−αo∗Bo∗∥2.\mathcal{E}_{rb} \leq \| \mathbf{W} - \alpha_{o}^* \mathbf{B}_{o}^* \|^2 .$

因此，采用残差近似的方法，相较于将显著权重保留为8位或16位，我们能够以超低位宽存储进一步减少显著权重的二值量化误差。

3.2 钟形分布拆分二值化

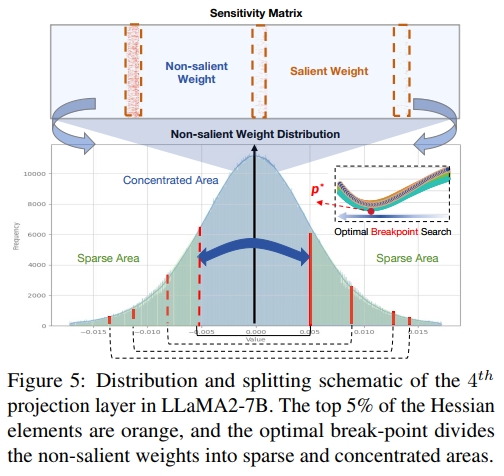
在剔除显著权重后，剩余的权重保持钟形分布，且随着显著权重影响的去除，分布变得更接近对称，如图5所示。二值量化作为极端的均匀量化方式，在非均匀分布下会带来更大的损失。一种实用的方法是根据权重分布进行分组量化（Park 等，2018；Fang 等，2020；Jain 等，2019）。在量化精度和压缩效率之间进行权衡，我们确定在分布中找到一个断点。图5展示了该划分将非显著的钟形分布分为两类：稀疏区域和集中区域。分割过程确定了一个断点，将非显著权重分为两组：集中权重 $A_c[-p, p]$ 和稀疏权重 $As[−m,−p]∪[p,m]A_s[-m, -p] \cup [p, m]$ ，其中 $m$ 表示非显著权重的最大范围。随后我们分别对 $A_c$ （集中区）和 $A_s$ （稀疏区）进行二值化。