招聘公务员问题

招聘公务员问题

问题1

复试因素集与评语集

复试因素集 U={知识面,理解能力,应变能力,表达能力}U = \{\text{知识面}, \text{理解能力}, \text{应变能力}, \text{表达能力}\}U={知识面,理解能力,应变能力,表达能力}

复试评语集 V={A,B,C,D}V = \{A, B, C, D\}V={A,B,C,D}，对应数值分别为 5, 4, 3, 2。

柯西分布隶属函数

$$f(x)=\{\begin{array}{ll}\left[0.3915\ln \left(\frac{x-1}{3-x}\right)+0.3699\right],& 1\le x\le 3\\ \frac{1.1086}{x}+0.8942,& 3<x\le 5\end{array}$$

当评价为 A时，隶属度为 1，即 $f(5)=1$；当评价为 C时，隶属度为 0.8，即 $f(3)=0.8$；当评价为 E时（未出现），隶属度为 0.01，即 $f(1)=0.01$。

判断矩阵

每位应聘者的判断矩阵为：

$$R_j=[r_{j1},r_{j2},r_{j3},r_{j4}],j=1,2,...,16$$

其中 $r_{j1}$ 表示第$j$位应聘者在“知识面”上的隶属度得分，依此类推。

权重与综合评价

假设因素集 $U$ 的各因素地位等同，权重为 $w=[0.25,0.25,0.25,0.25{]}^T$。

综合后的评价可以看作 $V$ 上的模糊向量：

$$B=w\cdot R$$

对初试成绩和复试成绩进行归一化处理，并计算综合得分：

$$s_j^{\prime }=\lambda a_j^{\prime }+(1-\lambda )b_j^{\prime },\lambda \in [0,1]$$

用人部门满意度评估

满意度评语集分为7个等级，对应数值为 7, 6, 5, 4, 3, 2, 1。

柯西分布隶属函数定义如下：

$$f(x)=\{\begin{array}{ll}\left[0.3574\ln \left(\frac{x-1}{4-x}\right)+0.3046\right],& 1\le x\le 4\\ \frac{1.4944}{x}+0.8413,& 4<x\le 7\end{array}$$

根据上述隶属函数，每个应聘者在各个部门的评分可以构成一个判断矩阵 $R$，并结合权重 $w=[0.25,0.25,0.25,0.25{]}^T$ 得到综合评价矩阵 $B$。

数学模型

决策变量 $x_{ij}$ 定义为：

$$x_{ij}=\{\begin{array}{ll}1,& \text{第 }j\text{ 位应聘者录用到第 }i\text{ 个人事部门}\\ 0,& \text{否则}\end{array}$$

目标是最大化综合得分：

$$\max z=\sum _{i=1}^7\sum _{j=1}^{16}(s_j^{\prime }{x}_{ij}+b_{ij})$$

约束条件包括确保每个应聘者最多被录用一次，以及各部门的人数限制。

import numpy as np
import pandas as pd
from ortools.linear_solver import pywraplp# =====================
# 数据读取与预处理
# =====================
# 读取应聘者数据 (16人)
applicants = np.loadtxt('招聘公务员笔试成绩，个人意愿，及专家面试评分.txt')
interview_scores = applicants[:, 3:7]  # 面试评分(4项能力)# 读取部门数据 (7个部门)
depts = np.loadtxt('用人部门的基本情况及对公务员的期望要求.txt')
dept_requirements = depts[:, 6:10]  # 部门要求(4项能力)# 读取综合得分 (16人)
s_j = np.loadtxt('应聘者的综合得分及排序.txt')# =====================
# 计算b_j^{(i)}矩阵
# =====================
# 满意度映射字典
satisfaction_map = {# 部门要求为A时(5, 5): 0.8,  # 基本满意(5, 4): 0.6514,  # 比较不满意(5, 3): 0.3499,  # 不满意(5, 2): 0.01,  # 非常不满意# 部门要求为B时(4, 5): 0.8797,  # 比较满意(4, 4): 0.8,  # 基本满意(4, 3): 0.6514,  # 比较不满意(4, 2): 0.3499,  # 不满意# 部门要求为C时(3, 5): 0.9449,  # 满意(3, 4): 0.8797,  # 比较满意(3, 3): 0.8,  # 基本满意(3, 2): 0.6514,  # 比较不满意# 部门要求为D时(2, 5): 1.0,  # 非常满意(2, 4): 0.9449,  # 满意(2, 3): 0.8797,  # 比较满意(2, 2): 0.8  # 基本满意
}# 计算b_j^{(i)}矩阵 (7部门×16应聘者)
b_matrix = np.zeros((7, 16))
for i in range(7):  # 遍历每个部门for j in range(16):  # 遍历每个应聘者total_score = 0for k in range(4):  # 遍历4项能力dept_req = dept_requirements[i, k]app_score = interview_scores[j, k]# 查找满意度量化值total_score += satisfaction_map.get((dept_req, app_score), 0)b_matrix[i, j] = total_score / 4  # 取平均# =====================
# 构建目标函数系数矩阵
# =====================
# 目标系数 = s_j + b_j^{(i)}
# s_j扩展为7×16矩阵 (每行相同)
s_matrix = np.tile(s_j, (7, 1))
objective_coeffs = s_matrix + b_matrix# =====================
# 建立0-1整数规划模型
# =====================
solver = pywraplp.Solver.CreateSolver('SCIP')
x = {}
n_depts = 7
n_apps = 16# 创建决策变量
for i in range(n_depts):for j in range(n_apps):x[i, j] = solver.IntVar(0, 1, f'x_{i}_{j}')# 约束1: 每个应聘者最多被一个部门录用
for j in range(n_apps):solver.Add(solver.Sum([x[i, j] for i in range(n_depts)]) <= 1)# 约束2: 每个部门录用1-2人
for i in range(n_depts):solver.Add(1 <= solver.Sum([x[i, j] for j in range(n_apps)]))solver.Add(solver.Sum([x[i, j] for j in range(n_apps)]) <= 2)# 约束3: 总共录用8人
solver.Add(solver.Sum([x[i, j] for i in range(n_depts) for j in range(n_apps)]) == 8)# 设置目标函数
objective = solver.Objective()
for i in range(n_depts):for j in range(n_apps):objective.SetCoefficient(x[i, j], objective_coeffs[i, j])
objective.SetMaximization()# =====================
# 求解模型
# =====================
status = solver.Solve()# =====================
# 结果处理与输出
# =====================
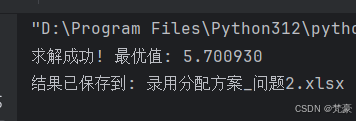
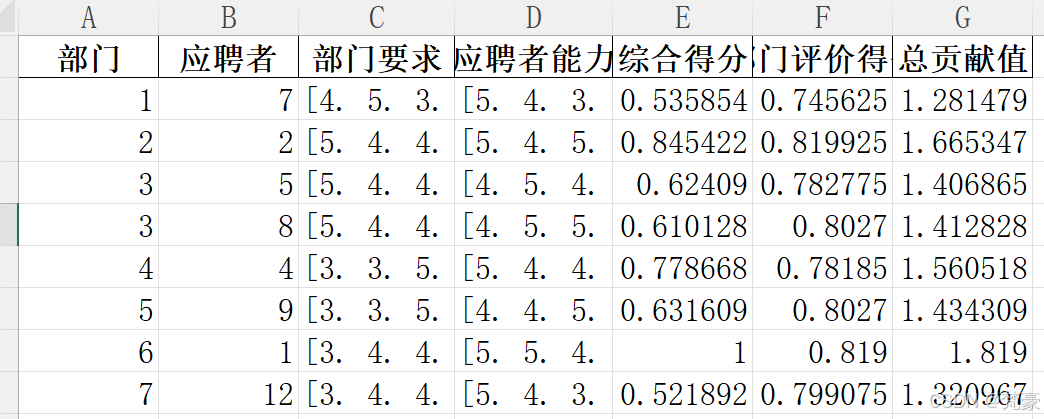
if status == pywraplp.Solver.OPTIMAL:# 创建分配结果表assignment = []for i in range(n_depts):for j in range(n_apps):if x[i, j].solution_value() > 0.5:assignment.append({'部门': i + 1,'应聘者': j + 1,'部门要求': dept_requirements[i],'应聘者能力': interview_scores[j],'综合得分': s_j[j],'部门评价得分': b_matrix[i, j],'总贡献值': objective_coeffs[i, j]})# 转换为DataFramedf_assignment = pd.DataFrame(assignment)# 计算最优值optimal_value = objective.Value()# 输出到Excelwith pd.ExcelWriter('录用分配方案.xlsx') as writer:# 分配方案表df_assignment.to_excel(writer, sheet_name='分配方案', index=False)# 最优值df_optimal = pd.DataFrame({'最优值': [optimal_value]})df_optimal.to_excel(writer, sheet_name='最优值', index=False)# 详细数据df_details = pd.DataFrame({'应聘者': np.arange(1, 17),'综合得分': s_j,**{f'能力{k + 1}': interview_scores[:, k] for k in range(4)}})df_details.to_excel(writer, sheet_name='应聘者数据', index=False)df_depts = pd.DataFrame({'部门': np.arange(1, 8),**{f'要求{k + 1}': dept_requirements[:, k] for k in range(4)}})df_depts.to_excel(writer, sheet_name='部门要求', index=False)print(f'求解成功! 最优值: {optimal_value:.6f}')print(f'结果已保存到: 录用分配方案.xlsx')
else:print('未找到最优解')

问题2

满意度评语集

满意度评语集分 3个等级：V={满意,比较满意,不满意}V = \{\text{满意}, \text{比较满意}, \text{不满意}\}V={满意,比较满意,不满意}，对应的量化值为$[1,0.6309,0]$。

柯西分布隶属函数

$$f(x)=0.9102\ln (4-x),3\le x\le 5$$

根据量化的评语集，每个应聘者 $j$ 对第 $i$ 个部门有一个满意度加权 $w_{ij}$，构造加权矩阵 $W=(w_{ij}{)}_{7\times 16}$。

综合满意度得分

因素集 U={福利待遇,工作条件,劳动强度,晋升机会,深造机会}U = \{\text{福利待遇}, \text{工作条件}, \text{劳动强度}, \text{晋升机会}, \text{深造机会}\}U={福利待遇,工作条件,劳动强度,晋升机会,深造机会}，满意度评语集分 3个等级，量化值为 $[1,0.6,0.1]$。

表2展示了不同部门的满意度得分，据此构建判断矩阵 $S=(s_{ki}{)}_{5\times 7}$ 并计算综合评价矩阵 $C$。

综合评价矩阵

构造对角矩阵 $diag(C)$ 和综合评价矩阵 $D$，使得 $d_{ij}=c_i{w}_{ij}$。

最终数学模型

基于双方的满意度要求，定义综合满意度得分为 $e_{ij}=b_{ij}{d}_{ij}$，并建立以下优化模型：

$$\max z=\sum _{i=1}^7\sum _{j=1}^{16}{e}_{ij}{x}_{ij}$$

约束条件确保每个应聘者至多被录用一次，且每个部门至少录取一名应聘者。

import numpy as np
import pandas as pd
from ortools.linear_solver import pywraplp# =====================
# 数据读取与预处理
# =====================
# 读取应聘者数据 (16人)
applicants = np.loadtxt('招聘公务员笔试成绩，个人意愿，及专家面试评分.txt')
# 第一列是笔试成绩，第二列第一志愿，第三列第二志愿，后面四列是面试评分
first_choice = applicants[:, 1].astype(int)  # 第一志愿（部门类别）
second_choice = applicants[:, 2].astype(int)  # 第二志愿（部门类别）
interview_scores = applicants[:, 3:7]  # 面试评分(4项能力)# 读取部门数据 (7个部门)
depts = np.loadtxt('用人部门的基本情况及对公务员的期望要求.txt')
dept_categories = depts[:, 0].astype(int)  # 部门类别（第一列）
dept_basic = depts[:, 1:6]  # 部门基本情况（5个指标）
dept_requirements = depts[:, 6:10]  # 部门要求(4项能力)# 读取综合得分 (16人) -- 问题2中不使用s_j，但保留备用
s_j = np.loadtxt('应聘者的综合得分及排序.txt')# =====================
# 计算b_j^{(i)}矩阵（部门对应聘者的满意度）
# =====================
satisfaction_map = {(5, 5): 0.8,  # 基本满意(5, 4): 0.6514,  # 比较不满意(5, 3): 0.3499,  # 不满意(5, 2): 0.01,  # 非常不满意(4, 5): 0.8797,  # 比较满意(4, 4): 0.8,  # 基本满意(4, 3): 0.6514,  # 比较不满意(4, 2): 0.3499,  # 不满意(3, 5): 0.9449,  # 满意(3, 4): 0.8797,  # 比较满意(3, 3): 0.8,  # 基本满意(3, 2): 0.6514,  # 比较不满意(2, 5): 1.0,  # 非常满意(2, 4): 0.9449,  # 满意(2, 3): 0.8797,  # 比较满意(2, 2): 0.8  # 基本满意
}b_matrix = np.zeros((7, 16))
for i in range(7):for j in range(16):total_score = 0for k in range(4):dept_req = dept_requirements[i, k]app_score = interview_scores[j, k]# 将部门要求和应聘者能力评分四舍五入为整数dept_req_int = int(round(dept_req))app_score_int = int(round(app_score))key = (dept_req_int, app_score_int)total_score += satisfaction_map.get(key, 0)b_matrix[i, j] = total_score / 4  # 取平均# =====================
# 计算c_i（部门总体满意度）
# =====================
# 权重向量
weights_basic = np.array([0.2, 0.2, 0.2, 0.2, 0.2])
# 计算每个部门的c_i
c_i = np.sum(dept_basic * weights_basic, axis=1)# =====================
# 计算w_ij（应聘者j对部门i的个人意愿满意度）
# =====================
# 满意度量化值：第一志愿=1.0, 第二志愿=0.6309, 其他=0.0
w_matrix = np.zeros((7, 16))
for i in range(7):dept_cat = dept_categories[i]  # 部门i的类别for j in range(16):if dept_cat == first_choice[j]:w_matrix[i, j] = 1.0elif dept_cat == second_choice[j]:w_matrix[i, j] = 0.6309else:w_matrix[i, j] = 0.0# =====================
# 计算d_ij = c_i * w_ij（应聘者对部门的满意度）
# =====================
d_matrix = np.zeros((7, 16))
for i in range(7):for j in range(16):d_matrix[i, j] = c_i[i] * w_matrix[i, j]# =====================
# 计算e_ij = sqrt(b_matrix * d_matrix)（综合满意度）
# =====================
e_matrix = np.sqrt(b_matrix * d_matrix)# =====================
# 建立0-1整数规划模型
# =====================
solver = pywraplp.Solver.CreateSolver('SCIP')
x = {}
n_depts = 7
n_apps = 16# 创建决策变量
for i in range(n_depts):for j in range(n_apps):x[i, j] = solver.IntVar(0, 1, f'x_{i}_{j}')# 约束1: 每个应聘者最多被一个部门录用
for j in range(n_apps):solver.Add(solver.Sum([x[i, j] for i in range(n_depts)]) <= 1)# 约束2: 每个部门录用1-2人
for i in range(n_depts):solver.Add(1 <= solver.Sum([x[i, j] for j in range(n_apps)]))solver.Add(solver.Sum([x[i, j] for j in range(n_apps)]) <= 2)# 约束3: 总共录用8人
solver.Add(solver.Sum([x[i, j] for i in range(n_depts) for j in range(n_apps)]) == 8)# 设置目标函数
objective = solver.Objective()
for i in range(n_depts):for j in range(n_apps):objective.SetCoefficient(x[i, j], e_matrix[i, j])
objective.SetMaximization()# =====================
# 求解模型
# =====================
status = solver.Solve()# =====================
# 结果处理与输出
# =====================
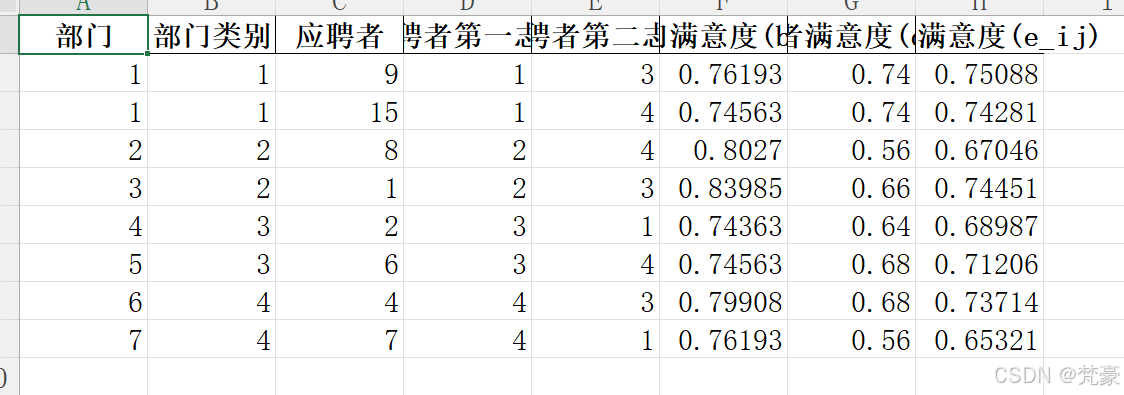
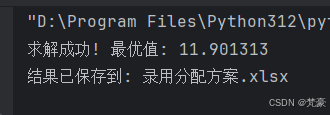
if status == pywraplp.Solver.OPTIMAL:# 创建分配结果表assignment = []for i in range(n_depts):for j in range(n_apps):if x[i, j].solution_value() > 0.5:assignment.append({'部门': i + 1,'部门类别': dept_categories[i],'应聘者': j + 1,'应聘者第一志愿': first_choice[j],'应聘者第二志愿': second_choice[j],'部门满意度(b_j)': b_matrix[i, j],'应聘者满意度(d_ij)': d_matrix[i, j],'综合满意度(e_ij)': e_matrix[i, j]})# 转换为DataFramedf_assignment = pd.DataFrame(assignment)# 计算最优值optimal_value = objective.Value()# 输出到Excelwith pd.ExcelWriter('录用分配方案_问题2.xlsx') as writer:# 分配方案表df_assignment.to_excel(writer, sheet_name='分配方案', index=False)# 最优值df_optimal = pd.DataFrame({'最优值': [optimal_value]})df_optimal.to_excel(writer, sheet_name='最优值', index=False)# 应聘者数据app_data = []for j in range(16):app_data.append({'应聘者': j + 1,'笔试成绩': applicants[j, 0],'第一志愿': first_choice[j],'第二志愿': second_choice[j],'知识面': interview_scores[j, 0],'理解能力': interview_scores[j, 1],'应变能力': interview_scores[j, 2],'表达能力': interview_scores[j, 3]})df_apps = pd.DataFrame(app_data)df_apps.to_excel(writer, sheet_name='应聘者数据', index=False)# 部门数据dept_data = []for i in range(7):dept_data.append({'部门': i + 1,'部门类别': dept_categories[i],'福利待遇': dept_basic[i, 0],'工作条件': dept_basic[i, 1],'劳动强度': dept_basic[i, 2],'晋升机会': dept_basic[i, 3],'深造机会': dept_basic[i, 4],'专业知识要求': dept_requirements[i, 0],'理解能力要求': dept_requirements[i, 1],'应变能力要求': dept_requirements[i, 2],'表达能力要求': dept_requirements[i, 3],'部门总体满意度(c_i)': c_i[i]})df_depts = pd.DataFrame(dept_data)df_depts.to_excel(writer, sheet_name='部门数据', index=False)# 综合满意度矩阵e_matrix_df = pd.DataFrame(e_matrix,index=[f'部门{i + 1}' for i in range(7)],columns=[f'应聘者{j + 1}' for j in range(16)])e_matrix_df.to_excel(writer, sheet_name='综合满意度矩阵')print(f'求解成功! 最优值: {optimal_value:.6f}')print(f'结果已保存到: 录用分配方案_问题2.xlsx')
else:print('未找到最优解')