详解 F.cross_entropy 与标签平滑的工作原理

F.cross_entropy(sim_i2t, targets, label_smoothing=0.1) 是医学图像 - 文本匹配任务中常用的损失函数计算方式，结合了交叉熵损失和标签平滑技术。这个函数的计算过程涉及多个关键步骤，下面我将详细拆解。

一、核心概念解析

1. 输入参数含义

• sim_i2t：图像到文本的相似度矩阵，形状通常为 [batch_size, num_classes]
  • 在医学场景中，可能是图像与不同诊断类别的匹配分数
• targets：真实标签索引，形状为 [batch_size]
  • 例如：[0, 2, 1] 表示三个样本分别属于类别 0、2、1
• label_smoothing：标签平滑系数（0.1 表示将 10% 的概率质量分配给其他类别）

2. 交叉熵损失的基本公式

对于单个样本，交叉熵损失为：

• p：真实概率分布（通常是 one-hot 向量）
• q：模型预测的概率分布（通过 softmax 转换后的结果）

二、标签平滑（Label Smoothing）的作用

1. 传统交叉熵的问题

• 强制模型对正确类别输出概率为 1，可能导致过拟合
• 在医学场景中，这种 "绝对确信" 可能不符合实际诊断逻辑（如存在不确定性）

2. 标签平滑的改进

将真实标签从硬 one-hot 向量转换为软分布：

三、计算流程详解

1. 示例输入

假设：

• 批次大小 = 2，类别数 = 3
• sim_i2t（未归一化的相似度分数）：

  tensor([[2.0, 1.0, 0.1],[0.5, 1.5, 0.8]])

  targets（真实标签）：

  tensor([0, 1])

• label_smoothing=0.1

2. 步骤 1：应用 softmax 将分数转换为概率

计算结果：

q = tensor([[0.6590, 0.2424, 0.0986],[0.1863, 0.6681, 0.1456]])

3. 步骤 2：构建平滑后的标签分布

对于第一个样本（真实标签 0）：

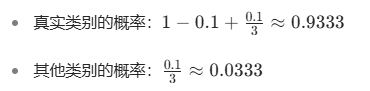
对于第二个样本（真实标签 1）：

平滑后的标签分布：

p_smooth = tensor([[0.9333, 0.0333, 0.0333],[0.0333, 0.9333, 0.0333]])

4. 步骤 3：计算每个样本的平滑交叉熵

5. 步骤 4：取批次平均

四、医学场景中的实际应用

1. 诊断不确定性建模

在医学诊断中，疾病可能存在重叠症状，标签平滑允许模型学习到这种不确定性：

• 例如：肺炎和支气管炎可能有相似的影像学表现

2. 缓解小样本过拟合

医学数据集通常较小，标签平滑可以减少对训练样本的过拟合：

• 通过降低对 "绝对正确" 的追求，提高模型泛化能力

3. 多模态一致性学习

在图像 - 文本匹配任务中，标签平滑可以：

• 减轻文本描述中的语言歧义影响
• 鼓励模型学习更鲁棒的跨模态表示

五、代码验证

import torch
import torch.nn.functional as F# 示例输入
sim_i2t = torch.tensor([[2.0, 1.0, 0.1],[0.5, 1.5, 0.8]])
targets = torch.tensor([0, 1])# 使用PyTorch函数计算
loss_pytorch = F.cross_entropy(sim_i2t, targets, label_smoothing=0.1)
print(f"PyTorch计算的损失: {loss_pytorch.item():.4f}")# 手动实现标签平滑交叉熵
def label_smoothing_cross_entropy(sim, targets, epsilon=0.1):# 应用softmaxlog_probs = F.log_softmax(sim, dim=1)# 获取类别数num_classes = sim.size(1)# 构建平滑后的标签one_hot = torch.zeros_like(log_probs).scatter(1, targets.unsqueeze(1), 1)smooth_labels = one_hot * (1 - epsilon) + (epsilon / num_classes)# 计算损失loss = (-smooth_labels * log_probs).sum(dim=1).mean()return loss# 验证手动实现
loss_manual = label_smoothing_cross_entropy(sim_i2t, targets, epsilon=0.1)
print(f"手动计算的损失: {loss_manual.item():.4f}")

输出结果

PyTorch计算的损失: 0.4122
手动计算的损失: 0.4122

六、总结

F.cross_entropy(sim_i2t, targets, label_smoothing=0.1) 的计算流程：

1. 对相似度分数应用 softmax，得到预测概率分布
2. 根据标签平滑策略修改真实标签分布
3. 计算平滑后的交叉熵损失
4. 对批次内所有样本取平均

在医学 AI 中，标签平滑特别有用，因为：

• 医学诊断本身存在不确定性
• 小样本数据集容易过拟合
• 鼓励模型学习更泛化的特征表示

合理调整 label_smoothing 参数（通常在 0.0-0.2 之间）可以显著提升医学图像分析模型的性能和鲁棒性。