算法训练营DAY37 第九章 动态规划 part05

完全背包理论基础-二维DP数组

完全背包

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

1. 确定dp数组以及下标的含义

dp[i][j] 表示从下标为[0-i]的物品，每个物品可以取无限次，放进容量为j的背包，价值总和最大是多少。

2. 确定递推公式

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

 分析dp[1][4]的推导过程，需要对比：目前背包容量为4，如果空出物品1的重量3，剩余重量为1的背包的最大价值+物品一的价值dp[i][j - weight[i]] + value[i]；目前背包容量为4，不装物品1，只装物品一之前的物品的最大价值dp[i - 1][j]。

所以递推公式为dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);

3. dp数组初始化

首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

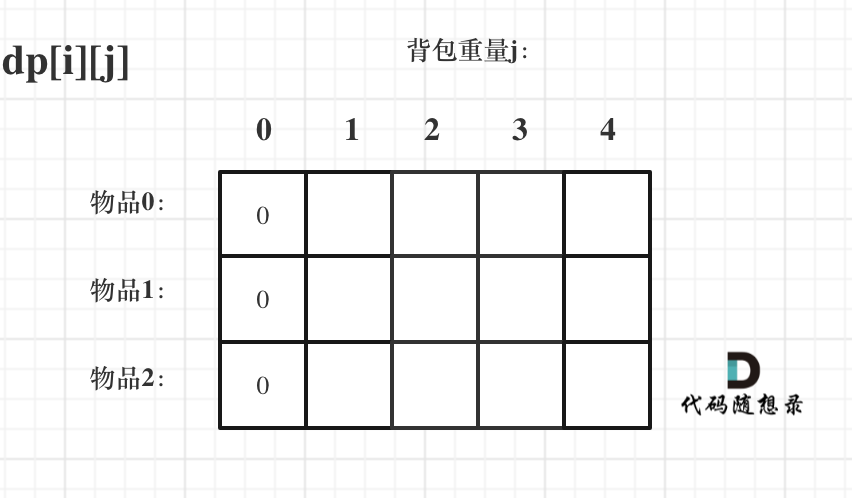
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]); 可以看出有一个方向 i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。

dp[0][j]，即：存放编号0的物品的时候，各个容量的背包所能存放的最大价值。 j < weight[0]的时候，dp[0][j] 应该是 0；当j >= weight[0]时，dp[0][j] 如果能放下weight[0]的话，就一直装，每一种物品有无限个。

4. 确定遍历顺序

先物品后背包或者先背包后物品都是可以的。

5. 举例推导dp数组

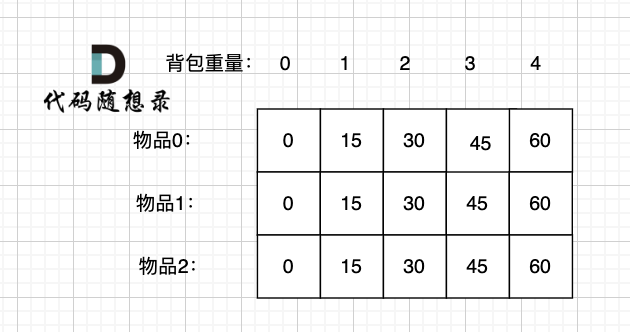
#include <iostream>
#include <vector>
using namespace std;int main() {int n, bagWeight;int w, v;cin >> n >> bagWeight;vector<int> weight(n);vector<int> value(n);for (int i = 0; i < n; i++) {cin >> weight[i] >> value[i];}vector<vector<int>> dp(n, vector<int>(bagWeight + 1, 0));// 初始化for (int j = weight[0]; j <= bagWeight; j++)dp[0][j] = dp[0][j - weight[0]] + value[0];for (int i = 1; i < n; i++) { // 遍历物品for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量if (j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);}}cout << dp[n - 1][bagWeight] << endl;return 0;
}

518.零钱兑换II

518. 零钱兑换 II - 力扣（LeetCode）

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:

• 输入: amount = 5, coins = [1, 2, 5]
• 输出: 4

解释: 有四种方式可以凑成总金额:

• 5=5
• 5=2+2+1
• 5=2+1+1+1
• 5=1+1+1+1+1

1、确定dp数组以及下标的含义

dp[i][j]：使用 下标为[0, i]的coins[i]能够凑满j（包括j）这么大容量的包，有dp[i][j]种组合方法。

2、确定递推公式

本题递推公式：dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]

dp[i][j]的计算方式等于:不加第i种硬币凑出j的数量+需要再加一个第i种硬币的数量，即

dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]]

3. dp数组如何初始化

二维数组的最上行 和 最左列一定要初始化，这是递推公式推导的基础，

dp[0][0]

应该是：背包空间为0，装满「物品0」 的组合数有多少呢？

应该是 0 个

dp[0][j] 

如果 j 可以整除 物品0，那么装满背包就有1种组合方法。

dp[i][0] 的含义：用物品i（即coins[i]） 装满容量为0的背包 有几种组合方法。

都有一种方法，即不装。

所以 dp[i][0] 都初始化为1

4. 确定遍历顺序

二维DP数组的完全背包的两个for循环先后顺序是无所谓的。

5. 打印DP数组

class Solution {
public:int change(int amount, vector<int>& coins) {int bagsize=amount;vector<vector<uint64_t>> dp(coins.size(),vector<uint64_t>(bagsize+1,0));for(int j=0;j<=bagsize;j++){if(j%coins[0]==0)dp[0][j]=1;}for(int i=0;i<coins.size();i++){dp[i][0]=1;}for(int i=1;i<coins.size();i++){for(int j=1;j<=bagsize;j++){if(coins[i]>j)dp[i][j]=dp[i-1][j];else{dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]];}}}return dp[coins.size()-1][bagsize];}
}; 

377. 组合总和 Ⅳ

377. 组合总和 Ⅳ

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);dp[0] = 1;for (int i = 0; i <= target; i++) { // 遍历背包for (int j = 0; j < nums.size(); j++) { // 遍历物品if (i - nums[j] >= 0 && dp[i] <= INT_MAX - dp[i - nums[j]]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
};

377. 组合总和 Ⅳ

给定一个由正整数组成且不存在重复数字的数组，找出和为给定目标正整数的组合的个数。

示例:

• nums = [1, 2, 3]
• target = 4

所有可能的组合为： (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)

请注意，顺序不同的序列被视作不同的组合。

因此输出为 7。

动规五部曲分析

1、确定dp数组以及下标的含义

dp[i]: 凑成目标正整数为i的排列个数为dp[i]

2、确定递推公式

dp[i]（考虑nums[j]）可以由 dp[i - nums[j]]（不考虑nums[j]） 推导出来。

dp[i] += dp[i - nums[j]];

3、dp数组初始化

因为递推公式dp[i] += dp[i - nums[j]]的缘故，dp[0]要初始化为1。非0下标的dp[i]应该初始为0，这样才不会影响dp[i]累加所有的dp[i - nums[j]]。

4、确定遍历顺序

数字不限制使用次数，完全背包

得到的集合是排列，所以要考虑元素之间的顺序。

组合数：外层物品内层背包

排列数：外层背包，内层物品

5、距离推导

70. 爬楼梯（进阶版）

卡码网：57. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

输入描述：输入共一行，包含两个正整数，分别表示n, m

输出描述：输出一个整数，表示爬到楼顶的方法数。

输入示例：3 2

输出示例：3

提示：

当 m = 2，n = 3 时，n = 3 这表示一共有三个台阶，m = 2 代表你每次可以爬一个台阶或者两个台阶。

此时你有三种方法可以爬到楼顶。

• 1 阶 + 1 阶 + 1 阶段
• 1 阶 + 2 阶
• 2 阶 + 1 

动规五部曲

1、确定dp数组以及下标的含义

dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法。

2、确定递推公式

dp[i] += dp[i - j]

3、dp数组初始化

dp[0] 一定为1，下标非0的dp[i]初始化为0。

4、确定遍历顺序

答案是要求排列，所以外层循环背包target；内层循环nums物品；

5、举例推导

#include <iostream>
#include <vector>
using namespace std;
int main(){int n,m;while(cin>>n>>m){vector<int> dp(n+1,0);dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(i-j>=0){dp[i]+=dp[i-j];}}}cout<<dp[n]<<endl;}
}