当前位置： 首页 > news >正文

【C++】stack和queue拓展学习

news 2025/7/22 9:36:32

目录

1.反向迭代器思路及实现

1.1. 源码及框架分析

1.2. 实现反向迭代器

2.stack和queue练习拓展-计算器实现

2.1. 后缀表达式概念

2.2. 后缀表达式运算规则

2.3. 中缀表达式转后缀表达式

2.3.1 转换思路

2.3.2 代码实现

2.4. 计算器实现

1.反向迭代器思路及实现

1.1. 源码及框架分析

SGI-STL30版本源代码，反向迭代器实现的核心源码在stl_iterator.h中。

前文我们了解到了正向迭代器是基于原生指针的封装实现，反向迭代器的逻辑与正向迭代器的逻辑正好相反，代码应该高度相似，因此在学习了stack与queue之后，明白了适配器思想，我们就复用正向迭代器代码实现反向迭代器，减少代码冗余。

下面我们截出vector和list的的反向迭代器结构框架核心部分截取出来如下：

// stl_list.h
template <class T, class Alloc = alloc>
class list {
public:typedef __list_iterator<T, T&, T*> iterator;typedef __list_iterator<T, const T&, const T*> const_iterator;
#ifdef __STL_CLASS_PARTIAL_SPECIALIZATIONtypedef reverse_iterator<const_iterator> const_reverse_iterator;typedef reverse_iterator<iterator> reverse_iterator;
#else /* __STL_CLASS_PARTIAL_SPECIALIZATION */typedef reverse_bidirectional_iterator<const_iterator, value_type,const_reference, difference_type> const_reverse_iterator;typedef reverse_bidirectional_iterator<iterator, value_type, reference,difference_type> reverse_iterator;
#endif /* __STL_CLASS_PARTIAL_SPECIALIZATION */iterator begin() { return (link_type)((*node).next); }const_iterator begin() const { return (link_type)((*node).next); }iterator end() { return node; }const_iterator end() const { return node; }reverse_iterator rbegin() { return reverse_iterator(end()); }const_reverse_iterator rbegin() const {returnconst_reverse_iterator(end());}reverse_iterator rend() { return reverse_iterator(begin()); }const_reverse_iterator rend() const {returnconst_reverse_iterator(begin());}
};
// stl_vector.h
template <class T, class Alloc = alloc>
class vector {
public:typedef T value_type;typedef value_type* iterator;
#ifdef __STL_CLASS_PARTIAL_SPECIALIZATIONtypedef reverse_iterator<const_iterator> const_reverse_iterator;typedef reverse_iterator<iterator> reverse_iterator;
#else /* __STL_CLASS_PARTIAL_SPECIALIZATION */typedef reverse_iterator<const_iterator, value_type, const_reference,difference_type> const_reverse_iterator;typedef reverse_iterator<iterator, value_type, reference, difference_type>reverse_iterator;
#endif /* __STL_CLASS_PARTIAL_SPECIALIZATION */iterator begin() { return start; }const_iterator begin() const { return start; }iterator end() { return finish; }const_iterator end() const { return finish; }reverse_iterator rbegin() { return reverse_iterator(end()); }const_reverse_iterator rbegin() const {returnconst_reverse_iterator(end());}reverse_iterator rend() { return reverse_iterator(begin()); }const_reverse_iterator rend() const {returnconst_reverse_iterator(begin());}
};
// stl_iterator.h
#ifdef __STL_CLASS_PARTIAL_SPECIALIZATION
// This is the new version of reverse_iterator, as defined in the
// draft C++ standard. It relies on the iterator_traits template,
// which in turn relies on partial specialization. The class
// reverse_bidirectional_iterator is no longer part of the draft
// standard, but it is retained for backward compatibility.
template <class Iterator>
class reverse_iterator
{
protected:Iterator current;
public:typedef typename iterator_traits<Iterator>::iterator_categoryiterator_category;typedef typename iterator_traits<Iterator>::value_typevalue_type;typedef typename iterator_traits<Iterator>::difference_typedifference_type;typedef typename iterator_traits<Iterator>::pointerpointer;typedef typename iterator_traits<Iterator>::referencereference;typedef Iterator iterator_type;typedef reverse_iterator<Iterator> self;
public:reverse_iterator() {}explicit reverse_iterator(iterator_type x) : current(x) {}reverse_iterator(const self& x) : current(x.current) {}
#ifdef __STL_MEMBER_TEMPLATEStemplate <class Iter>reverse_iterator(const reverse_iterator<Iter>& x) : current(x.current) {}
#endif /* __STL_MEMBER_TEMPLATES */iterator_type base() const { return current; }reference operator*() const {Iterator tmp = current;return *--tmp;}
#ifndef __SGI_STL_NO_ARROW_OPERATORpointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */self& operator++() {--current;return *this;}self operator++(int) {self tmp = *this;--current;return tmp;}self& operator--() {++current;return *this;}self operator--(int) {self tmp = *this;++current;return tmp;}self operator+(difference_type n) const {return self(current - n);}self& operator+=(difference_type n) {current -= n;return *this;}self operator-(difference_type n) const {return self(current + n);}self& operator-=(difference_type n) {current += n;return *this;}reference operator[](difference_type n) const { return *(*this + n); }
};
template <class Iterator>
inline bool operator==(const reverse_iterator<Iterator>& x,const reverse_iterator<Iterator>& y) {return x.base() == y.base();
}
template <class Iterator>
inline bool operator<(const reverse_iterator<Iterator>& x,const reverse_iterator<Iterator>& y) {return y.base() < x.base();
}
template <class Iterator>
inline typename reverse_iterator<Iterator>::difference_type
operator-(const reverse_iterator<Iterator>& x,const reverse_iterator<Iterator>& y) {return y.base() - x.base();
}
template <class Iterator>
inline reverse_iterator<Iterator>
operator+(reverse_iterator<Iterator>::difference_type n,const reverse_iterator<Iterator>& x) {return reverse_iterator<Iterator>(x.base() - n);
}
#else /* __STL_CLASS_PARTIAL_SPECIALIZATION */
// This is the old version of reverse_iterator, as found in the original
// HP STL. It does not use partial specialization.
template <class BidirectionalIterator, class T, class Reference = T&,class Distance = ptrdiff_t>
class reverse_bidirectional_iterator {typedef reverse_bidirectional_iterator<BidirectionalIterator, T, Reference,Distance> self;
protected:BidirectionalIterator current;
public:typedef bidirectional_iterator_tag iterator_category;typedef T value_type;typedef Distance difference_type;typedef T* pointer;typedef Reference reference;reverse_bidirectional_iterator() {}explicit reverse_bidirectional_iterator(BidirectionalIterator x): current(x) {}BidirectionalIterator base() const { return current; }Reference operator*() const {BidirectionalIterator tmp = current;return *--tmp;}
#ifndef __SGI_STL_NO_ARROW_OPERATORpointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */self& operator++() {--current;return *this;}self operator++(int) {self tmp = *this;--current;return tmp;}self& operator--() {++current;return *this;}self operator--(int) {self tmp = *this;++current;return tmp;}
};
template <class RandomAccessIterator, class T, class Reference = T&,class Distance = ptrdiff_t>
class reverse_iterator {typedef reverse_iterator<RandomAccessIterator, T, Reference, Distance>self;
protected:RandomAccessIterator current;
public:typedef random_access_iterator_tag iterator_category;typedef T value_type;typedef Distance difference_type;typedef T* pointer;typedef Reference reference;reverse_iterator() {}explicit reverse_iterator(RandomAccessIterator x) : current(x) {}RandomAccessIterator base() const { return current; }Reference operator*() const { return *(current - 1); }
#ifndef __SGI_STL_NO_ARROW_OPERATORpointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */self& operator++() {--current;return *this;}self operator++(int) {self tmp = *this;--current;return tmp;}self& operator--() {++current;return *this;}self operator--(int) {self tmp = *this;++current;return tmp;}self operator+(Distance n) const {return self(current - n);}self& operator+=(Distance n) {current -= n;return *this;}self operator-(Distance n) const {return self(current + n);}self& operator-=(Distance n) {current += n;return *this;}Reference operator[](Distance n) const { return *(*this + n); }
};
#endif //__STL_CLASS_PARTIAL_SPECIALIZATION

• 源码中我们可以看到reverse_iterator实现了两个版本，通过
__STL_CLASS_PARTIAL_SPECIALIZATION 条件编译控制使用哪个版本，在旧版本中，因为因为封装是类型不好确定，我们需要自己传递参数，而有了萃取技术后，我们可以得到对应的类型，因此就不需要传递很多参数。

简单点说就是支持偏特化的迭代器萃取以后，反向迭代器使用的是这个版本， template <class Iterator>class reverse_iterator（一个参数）; 之前使用的是template <class BidirectionalIterator, class T, class Reference,class Distance>class reverse_bidirectional_iterator;template <class RandomAccessIterator, class T, class Reference,class Distance>class reverse_iterator;（多个参数）


• 我们可以看到他们的差别主要是在模板参数是否传递迭代器指向的数据类型，支持偏特化的迭代器萃取以后就不需要给了，因为reverse_iterator 内部可以通过迭代器萃取获取数据类型。迭代器萃取的本质是一个特化（这里我们就不讲解了），想了解可以去看源码。

本文这里我们为了便于理解，我们主要使用模版参数传递数据类型的方式实现。


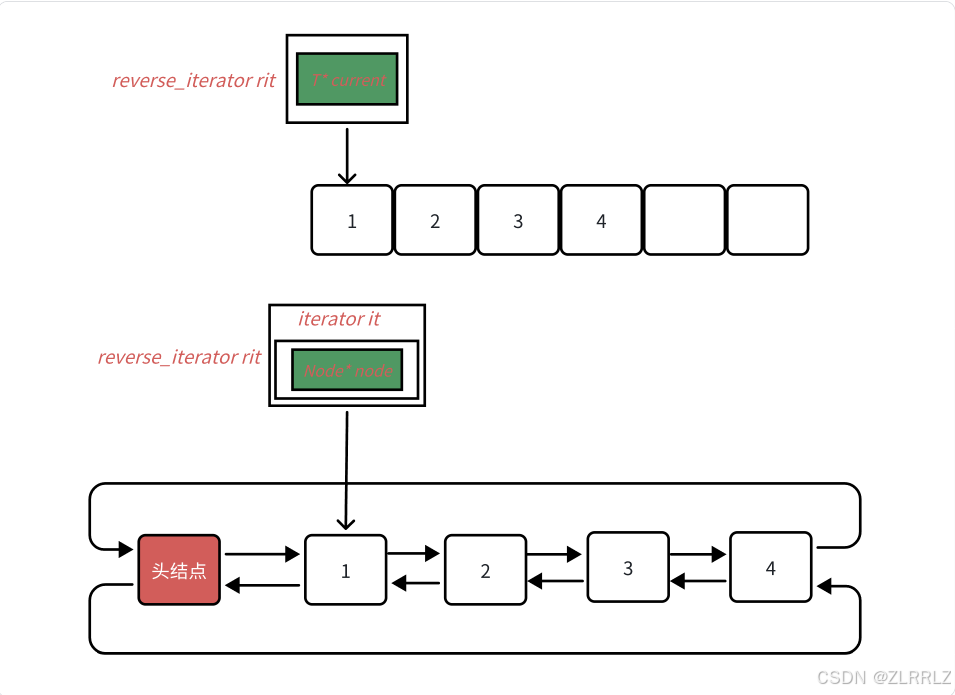
• 反向迭代器本质是一个适配器，使用模版实现，传递哪个容器的迭代器就可以封装适配出对应的反向迭代器。因为反向迭代器的功能跟正向的迭代器功能高度相似，只是遍历的方向相反，类似operator++ 底层调用迭代器的operator-- 等，所以封装一下就可以实现。


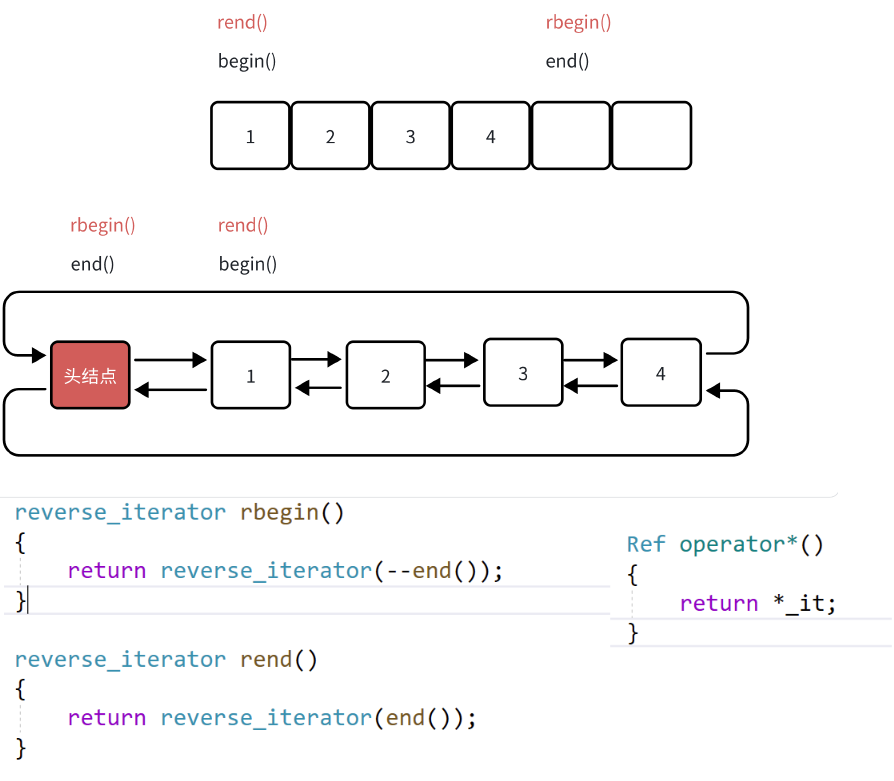
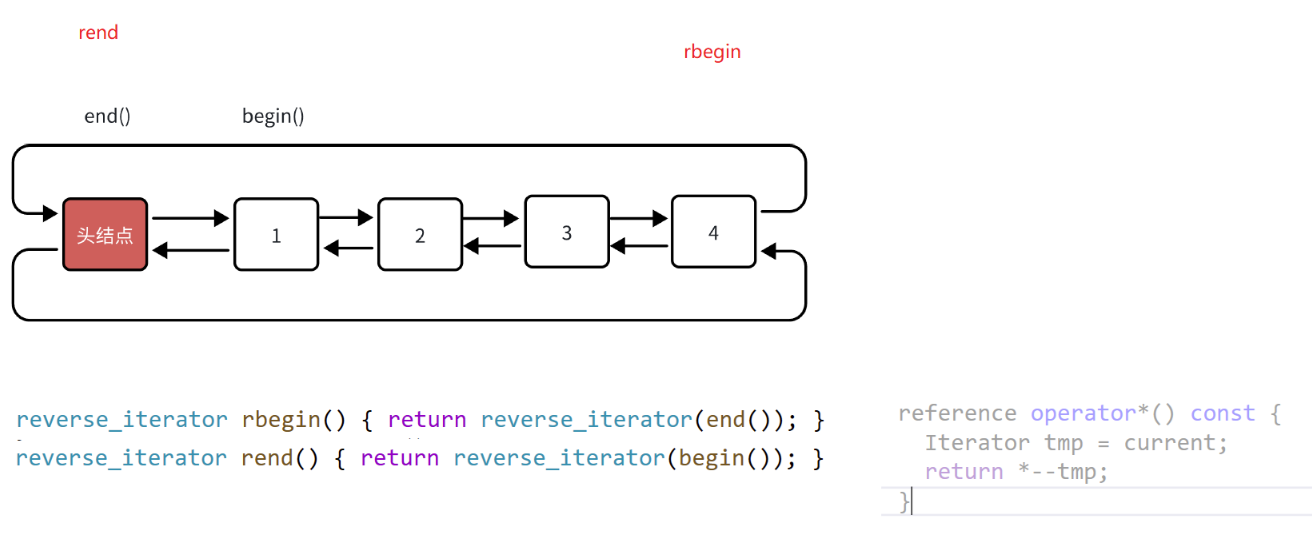
• 比较奇怪的是operator*的实现，源码内部访问的是迭代器当前位置的前一个位置。

这个要结合容器中rbegin和rend实现才能看懂，rbegin返回的是封装end位置的反向迭代器，rend返回的是封装begin位置迭代器的反向迭代器，这里是为了与正向迭代器对应，专门实现出一个对称版本，begin与rend，end与rbegin，所以解引用访问的是当前位置的前一个位置，这样返回解引用rbegin时，返回上一个节点，即返回有效节点的最后一个节点，解引用rend就会正好返回哨兵节点。（这里没有其他的特殊作用，如果愿意也可以不对称实现）

1.2. 实现反向迭代器

// ReverseIterator.h
// 所有容器的反向迭代器
// 迭代器适配器
namespace zlr
{template<class Iterator, class Ref, class Ptr>struct ReverseIterator{typedef ReverseIterator<Iterator, Ref, Ptr> Self;// 正向迭代器Iterator _it;ReverseIterator(Iterator it):_it(it){}Ref operator*(){Iterator tmp = _it;return *(--tmp);}Ptr operator->(){return &(operator*());}Self& operator++(){--_it;return *this;}Self& operator--(){++_it;return *this;}Self operator++(int){Self tmp(*this);--_it;return tmp;}Self operator--(int){Self tmp(*this);--_it;return tmp;}bool operator!=(const Self& s) const{return _it != s._it;}bool operator==(const Self& s) const{return _it != s._it;}};
}
// vector.h
#include"ReverseIterator.h"
namespace zlr
{template<class T>class vector{public:typedef T* iterator;typedef const T* const_iterator;typedef ReverseIterator<iterator, T&, T*> reverse_iterator;typedef ReverseIterator<const_iterator, const T&, const T*>const_reverse_iterator;reverse_iterator rbegin(){return reverse_iterator(end());}reverse_iterator rend(){return reverse_iterator(begin());}const_reverse_iterator rbegin() const{return const_reverse_iterator(end());}const_reverse_iterator rend() const{return const_reverse_iterator(begin());}iterator begin(){return _start;}iterator end(){return _finish;}const_iterator begin() const{return _start;}const_iterator end() const{return _finish;}// ....private:iterator _start = nullptr;iterator _finish = nullptr;iterator _endofstorage = nullptr;};
}
// list.h
#include"ReverseIterator.h"
namespace zlr
{template<class T>class list{typedef ListNode<T> Node;public:typedef ListIterator<T, T&, T*> iterator;typedef ListIterator<T, const T&, const T*> const_iterator;typedef ReverseIterator<iterator, T&, T*> reverse_iterator;typedef ReverseIterator<const_iterator, const T&, const T*>const_reverse_iterator;reverse_iterator rbegin(){return reverse_iterator(end());}reverse_iterator rend(){return reverse_iterator(begin());}const_reverse_iterator rbegin() const{return const_reverse_iterator(end());}const_reverse_iterator rend() const{return const_reverse_iterator(begin());}iterator begin(){return _head->_next;}iterator end(){return _head;}const_iterator begin() const{return _head->_next;}const_iterator end() const{return _head;}// ...private:Node* _head;size_t _size;};
}
// test.cpp
#include"list.h"
#include"vector.h"
int main()
{zlr::list<int> lt = { 1,2,3,4 };zlr::list<int>::reverse_iterator rit = lt.rbegin();while (rit != lt.rend()){//*rit = 1;cout << *rit << " ";++rit;}cout << endl;return 0;
}
//int main()
//{
// zlr::vector<int> v = { 1,2,3,4 };
// zlr::vector<int>::reverse_iterator rit = v.rbegin();
// while (rit != v.rend())
// {
// //*rit = 1;
// cout << *rit << " ";
// ++rit;
// }
// cout << endl;
//
// return 0;
//}

2.stack和queue练习拓展-计算器实现

2.1. 后缀表达式概念

• 我们日常写的计算表达式都是中缀表达式，也就是运算符在中间，运算数在两边，但是中缀表达式直接读取无法马上进行运算，因为一个计算表达式还涉及运算符优先级问题，中缀表达式无法直接确定一个运算符优先级，必须根据相邻运算符才能确定。如： 1-2*(3-4)+5 中遇到-和*都无法运算，因为后面还有括号优先级更高。


• 所以其中一种实现思路是把中缀表达式转换为后缀表达式，也就是说分析计算表达式的优先级，将运算符放到前面，运算符放到运算数的后面，然后我们依次读取后缀表达式，遇到运算符就可以进行运算了。后缀表达式也就做逆波兰表达式(Reverse Polish Notation, RPN)，这种表示法由波兰逻辑学家J·卢卡西维兹于1929年提出，后来被广泛应用于计算机科学中。

2.2. 后缀表达式运算规则

• 后缀表达式因为已经确定好优先级，运算符方式非常简单，就是遇到运算符时，取前面的两个数进行运算，因为经过中缀转后缀优先级已经确定好了，因此我们根据运算特点，使用栈来实现。


• 建立一个栈存储运算数，读取后缀表达式，遇到运算数入栈；遇到运算符，出栈顶的两个数据进行运算，运算后将结果作为一个运算数入栈继续参与下一次的运算。读取表达式结束后，最后栈里面的值就是运算结果。

  • 150. 逆波兰表达式求值 - 力扣（LeetCode）​​​​​​ 

class Solution {
public:int evalRPN(const vector<string>& tokens) {stack<int> s;for (size_t i = 0; i < tokens.size(); ++i){const string& str = tokens[i];// str为运算数，入栈if (!("+" == str || "-" == str || "*" == str || "/" == str)){s.push(stoi(str));}else{// str为运算符，取前两个运算数进行运算int right = s.top();s.pop();int left = s.top();s.pop();switch (str[0]){case '+':s.push(left + right);break;case '-':s.push(left - right);break;case '*':s.push(left * right);break;case '/':s.push(left / right);break;}}}return s.top();}
};

2.3. 中缀表达式转后缀表达式

2.3.1 转换思路

• 依次读取计算表达式中的值，遇到运算数直接输出。


• 建立一个栈存储运算符，利用栈后进新出性质，遇到后面运算符，出栈里面存的前面运算符进行比较，确定优先级。


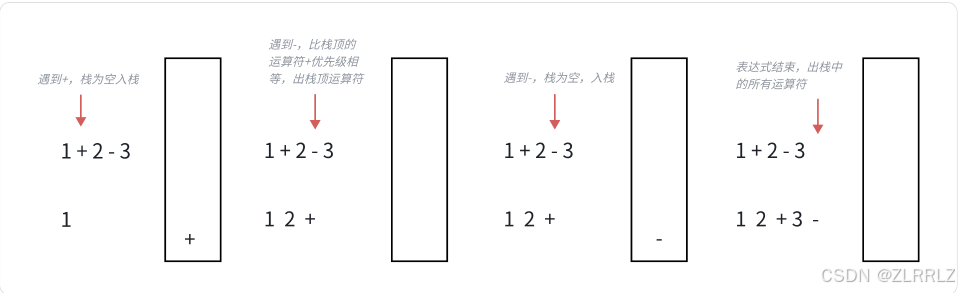
• 遇到运算符，如果栈为空或者栈不为空且当前运算符比栈顶运算符优先级高，则当前运算符入栈。因为如果栈里面存储的是前一个运算符，当前运算符比前一个优先级高，说明前一个不能运算，当前运算符也不能运算，因为后面可能还有更高优先级的运算符。


• 遇到运算符，如果栈不为为空且当前运算符比栈顶运算符优先级低或相等，说明栈顶的运算符可以运算了，则输出栈顶运算符，当前运算符继续走前面遇到运算符的逻辑。


• 如果遇到()，则把括号的计算表达式当成一个子表达式，进行递归，跟上思路类似处理子表达式，处理后转换出的后缀表达式加在前面表达式的后面即可。


• 计算表达式或者()中子表达式结束时，输出栈中所有运算符。

2.3.2 代码实现

class Solution {
public://map<char, int> _operatorPrecedence = { { '+', 1 }, { '-', 1 }, { '*', 2//}, { '/', 2 } };//因为运算符优先级与ASCII无关，这里我们使用结构体来处理运算符的优先级比较问题//如果学习过map容器，可以使用map处理int operatorPrecedence(char ch){struct opPD{char _op;int _pd;};static opPD arr[] = { {'+', 1},{'-', 1},{'*', 2},{'/', 2} };for (auto& e : arr){if (e._op == ch){return e._pd;}}assert(false);return -1;}//因为有递归的情况存在，我们这里使用i来记录当前访问位置void toRPN(const string& s, size_t& i, vector<string>& v){stack<char> st;while (i < s.size()){if (isdigit(s[i])){// 操作数输出string num;while (i < s.size() && isdigit(s[i])){num += s[i];++i;}v.push_back(num);}else{if (s[i] == '('){// 递归方式处理括号中的子表达式++i;toRPN(s, i, v);}else if (s[i] == ')'){++i;// 栈中的运算符全部输出while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}// 结束递归return;}else{// 运算符// 1、如果栈为空或者栈不为空且当前运算符比栈顶运算符优先级高，则当//前运算符入栈// 2、如果栈不为为空且比栈顶运算符优先级低或相等，说明栈顶的运算符//可以运算了，// 输出栈顶运算符，当前运算符继续走前面遇到运算符的逻辑if (st.empty() || operatorPrecedence(s[i]) >operatorPrecedence(st.top())){st.push(s[i]);++i;}else{v.push_back(string(1, st.top()));st.pop();}}}}// 栈中的运算符全部输出while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}}
};
int main()
{size_t i = 0;vector<string> v;//string str = "1+2-3";string str = "1+2-(3*4+5)-7";Solution().toRPN(str, i, v);for (auto& e : v){cout << e << " ";}cout << endl;return 0;
}

2.4. 计算器实现

 • 224. 基本计算器 - 力扣（LeetCode） 

• 有了上面两个部分学习之后，计算器OJ的大部分问题就解决了，但是这里还有一些问题需要处理。因为OJ中给的中缀表达式是字符串，字符串中包含空格，需要去掉空格。


• 其次就是负数和减号，要进行区分，将所有的负数-x转换为0-x，因为我们实现的代码考虑到乘除的情况，针对括号内的符号，我们不能直接变号处理。

class Solution {
public://map<char, int> _operatorPrecedence = { { '+', 1 }, { '-', 1 }, { '*', 2
}, { '/', 2 } };
int operatorPrecedence(char ch)
{struct opPD{char _op;int _pd;};static opPD arr[] = { {'+', 1},{'-', 1},{'*', 2},{'/', 2} };for (auto& e : arr){if (e._op == ch){return e._pd;}}assert(false);return -1;
}
void toRPN(const string& s, size_t& i, vector<string>& v)
{stack<char> st;while (i < s.size()){if (isdigit(s[i])){// 运算数输出string num;while (i < s.size() && isdigit(s[i])){num += s[i];++i;}v.push_back(num);}else{if (s[i] == '('){// 递归方式处理括号中的子表达式++i;toRPN(s, i, v);}else if (s[i] == ')'){++i;// 栈中的运算符全部输出while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}// 结束递归return;}else{// 运算符// 1、如果栈为空或者栈不为空且当前运算符比栈顶运算符优先级高，则当//前运算符入栈// 2、如果栈不为为空且比栈顶运算符优先级低或相等，说明栈顶的运算符//可以运算了，// 输出栈顶运算符，当前运算符继续走前面遇到运算符的逻辑if (st.empty() || operatorPrecedence(s[i]) >operatorPrecedence(st.top())){st.push(s[i]);++i;}else{v.push_back(string(1, st.top()));st.pop();}}}}// 栈中的运算符全部输出while (!st.empty()){v.push_back(string(1, st.top()));st.pop();}
}
int evalRPN(const vector<string>& tokens) {stack<int> s;for (size_t i = 0; i < tokens.size(); ++i){const string& str = tokens[i];// str为数字if (!("+" == str || "-" == str || "*" == str || "/" == str)){s.push(stoi(str));}else{// str为操作符int right = s.top();s.pop();int left = s.top();s.pop();switch (str[0]){case '+':s.push(left + right);break;case '-':s.push(left - right);break;case '*':s.push(left * right);break;case '/':s.push(left / right);break;}}}return s.top();
}
int calculate(string s)
{// 1、去除所有空格，否则下面的一些逻辑没办法处理std::string news;news.reserve(s.size());for (auto ch : s){if (ch != ' ')news += ch;}s.swap(news);news.clear();// 2、将所有的负数-x转换为0-xfor (size_t i = 0; i < s.size(); ++i){//当-的前一个字符不为运算数时，我们才添加"0-",否则就是减号，不需要处理//同时因为这里是下标比较，需要注意符号在表达式第一位的情况，防止越界if (s[i] == '-' && (i == 0 || (!isdigit(s[i - 1]) && s[i - 1] !=')')))news += "0-";elsenews += s[i];}// 中缀表达式转成后缀表达式size_t i = 0;vector<string> v;toRPN(news, i, v);// 后缀表达式进行运算return evalRPN(v);
}
};
http://www.lryc.cn/news/595118.html

相关文章：

  • DevCon 6记录
  • 从 “能用“ 到 “好用“：中小制造企业数字化转型中的 IT 系统优化管理策略
  • 扬声器测试解决方案
  • AWS Certified Cloud Practitioner 认证考试总结
  • Centos安装最新docker以及ubuntu安装docker
  • 旋转目标检测（Rotated Object Detection）技术概述
  • ESP32-S3学习笔记＜1＞：ESP-IDF的安装与命令
  • 【编程语言】C、C++、C#深度对比：三种语言的演进历程与应用场景
  • Windows VS2019 编译 Apache Thrift 0.15.0
  • 倒排索引实操
  • CS231n-2017 Lecture4神经网络笔记
  • selenium爬取图书信息
  • 通信刚需小能手，devicenet转PROFINET网关兼容物流分拣自动化
  • 从cv610的demo原理看，i2c的上拉电阻为 1k
  • day27 力扣332.重新安排行程 力扣51. N皇后 力扣37. 解数独 力扣455.分发饼干 力扣376. 摆动序列 力扣53. 最大子序和
  • 【设计模式C#】工厂方法模式（相比简单工厂模式更加具有灵活性和扩展性的工厂模式）
  • 力扣15:三数之和
  • 测量误差溯源：系统误差与随机误差的数学建模与分离方法
  • 结构型模式-架构解耦与扩展实践
  • 清理磁盘空间
  • Windows容器网络的带宽限制QoS策略配置
  • CPO光模块能取代传统光模块吗？
  • 量子算法可视化工具：撕裂量子黑箱的破壁者
  • 量子生成对抗网络：量子计算与生成模型的融合革命
  • 云原生安全工具：数字基础设施的免疫长城
  • 苹果Find My新增智能位置共享模式​​
  • 自动化计算机经过加固后有什么好处？
  • Android开发中ANR治理方案
  • Java -- 自定义异常--Wrapper类--String类
  • ansible批量部署zabbix客户端