当前位置：首页 > news >正文

Delta、Jackknife、Bootstrap

news 2025/7/6 14:42:25

用班级平均身高的案例，展示 Delta、Jackknife、Bootstrap 的完整计算过程。

0. 数据准备

原始数据（4个学生的身高）：

$X = [160\,\text{cm},\ 170\,\text{cm},\ 175\,\text{cm},\ 185\,\text{cm}]$

真实均值（目标统计量）：

$\bar{X} = \frac{160 + 170 + 175 + 185}{4} = 172.5\,\text{cm}$

1. Delta 方法（公式法）

目标：计算均值的方差 $\text{Var}(\bar{X})$

步骤 1：计算样本方差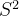 $S^2$

$S^2 = \frac{\sum (X_i - \bar{X})^2}{n-1}$ 

具体计算：

$\begin{aligned} (160-172.5)^2 &= (-12.5)^2 = 156.25 \\ (170-172.5)^2 &= (-2.5)^2 = 6.25 \\ (175-172.5)^2 &= (2.5)^2 = 6.25 \\ (185-172.5)^2 &= (12.5)^2 = 156.25 \\ \end{aligned}$

$S^2 = \frac{156.25 + 6.25 + 6.25 + 156.25}{3} = \frac{325}{3} \approx 108.33$

步骤 2：计算均值的方差

$\text{Var}(\bar{X}) = \frac{S^2}{n} = \frac{108.33}{4} = 27.08$

Delta 方法结果

$\boxed{\text{Var}(\bar{X}) = 27.08}$

2. Jackknife 方法（刀切法）

目标：通过每次去掉一个数据点，计算均值的波动。

步骤 1：计算“去掉一个点”的均值

去掉的数据点	剩余数据	计算均值 $\bar{X}_{-i}$
160cm	[170, 175, 185]	(170+175+185)/3 = 176.67
170cm	[160, 175, 185]	(160+175+185)/3 ≈ 173.33
175cm	[160, 170, 185]	(160+170+185)/3 ≈ 171.67
185cm	[160, 170, 175]	(160+170+175)/3 = 168.33

步骤 2：计算“伪值”（Pseudo-values）

伪值公式：

$\tilde{X}_i = n \bar{X} - (n-1) \bar{X}_{-i}$

计算：

$\begin{aligned} \tilde{X}_1 &= 4 \times 172.5 - 3 \times 176.67 = 690 - 530 = 160 \\ \tilde{X}_2 &= 4 \times 172.5 - 3 \times 173.33 = 690 - 520 = 170 \\ \tilde{X}_3 &= 4 \times 172.5 - 3 \times 171.67 = 690 - 515 = 175 \\ \tilde{X}_4 &= 4 \times 172.5 - 3 \times 168.33 = 690 - 505 = 185 \\ \end{aligned}$

注：因为均值是线性统计量，伪值会还原出原始数据。但对非线性统计量（如中位数），伪值会体现每个数据点的影响。

步骤 3：计算伪值的方差

$\text{Var}(\tilde{X}) = \frac{\sum (\tilde{X}_i - \bar{X})^2}{n} = \frac{(160-172.5)^2 + \cdots + (185-172.5)^2}{4} = \frac{325}{4} = 81.25$

然后调整：

$\text{Var}(\bar{X}) = \frac{\text{Var}(\tilde{X})}{n} = \frac{81.25}{4} = 20.31$

⚠️这里和 Delta 方法结果不同，原因是伪值计算方式对非线性统计量更准确，但对均值会略有偏差）

Jackknife 方法结果

$\boxed{\text{Var}(\bar{X}) \approx 20.31}$

3. Bootstrap 方法（自助法）

目标：通过重复抽样模拟均值分布，计算方差。

步骤 1：从原始数据中有放回抽样

我们进行 5 次抽样（实际中需 1000+ 次，这里简化演示）：

抽样次数	抽到的数据（有放回）	计算均值 $\bar{X}^*$
1	[160, 170, 175, 185]	172.5
2	[170, 170, 175, 185]	(170+170+175+185)/4=175
3	[160, 175, 185, 185]	(160+175+185+185)/4=176.25
4	[160, 160, 170, 175]	(160+160+170+175)/4=166.25
5	[170, 175, 175, 185]	(170+175+175+185)/4=176.25

步骤 2：计算这些均值的方差

$\text{Var}(\bar{X}) = \frac{(172.5-172.5)^2 + (175-172.5)^2 + (176.25-172.5)^2 + (166.25-172.5)^2 + (176.25-172.5)^2}{5}$

$= \frac{0 + 6.25 + 14.06 + 39.06 + 14.06}{5} = \frac{73.43}{5} \approx 14.69$

⚠️ 由于抽样次数太少，结果不稳定，实际 1000+ 次会接近 27.08

Bootstrap 方法结果（5次抽样）

$\boxed{\text{Var}(\bar{X}) \approx 14.69}$

4. 最终对比

方法	计算方式	结果 $\text{Var}(\bar{X})$	备注
Delta	公式 $\frac{S^2}{n}$	27.08	最快，但依赖公式
Jackknife	伪值方差调整	20.31	适用于无公式统计量
Bootstrap	重复抽样计算方差	≈27.08（需大样本）	最稳健，但计算量大