R实验 随机变量及其分布
- 实验目的:
- 掌握常见几种离散性随机变量及其分布在R语言中对应的函数用法;
- 掌握常见几种连续性随机变量及其分布在R语言中对应的函数用法;
- 掌握统计量的定义及统计三大抽样分布在R语言中对应的函数用法。
实验内容:
(习题4.5)通过对学生成绩的统计,高等数学课程的不及格率为20%。现随机地抽查了学习该课程的20名学生,试计算:(提示:这是一个二项分布,参考例4.7)
(1)有2名或2名以下学生不及格的概率是多少?(提示:累积分布函数pbinom(),答案:0.2061)
p1<-pbinom(2,size = 20,prob = 0.2)p1
(2)有4名学生不及格的概率是多少?(提示:概率密度函数dbinom(),答案:0.2182)
p2<-dbinom(4,size = 20,prob = 0.2)p2
(3)超过3名学生不及格的概率是多少?(提示:累积分布函数pbinom(),答案:0.5886)
p3<-pbinom(3,size = 20,prob = 0.2)p4<-1 - p3p4
(习题4.14)设某城市男子的身高服从均值为168cm,标准差为6cm的正态分布。求:
(1)该市男子身高在170cm以上的概率;(提示:累积分布函数pnorm(),答案:0.3694)
p<-pnorm(170,mean = 168,6)p1<-1-pp1
(2)为了使99%以上的男子上公共汽车不至于在车门上沿碰头,当地的公共汽车门框应设计多高?(提示:即求身高为哪个值以下的概率超过0.99,亦即:求k的值,使得P{X≤k}≥.0.99。显然题目是求分位数k,需要用到分位数函数qnorm()。注意到在R语言中,分位数函数默认是下分位数,大家可以看一下,R语言中下分位数函数中有一个参数lower.tail=TRUE,这个参数就是表示下分位数,默认值为TRUE。可参考例4.14。答案:181.9581)
p<-pnorm(170,mean = 168,6)p1<-1-pp1
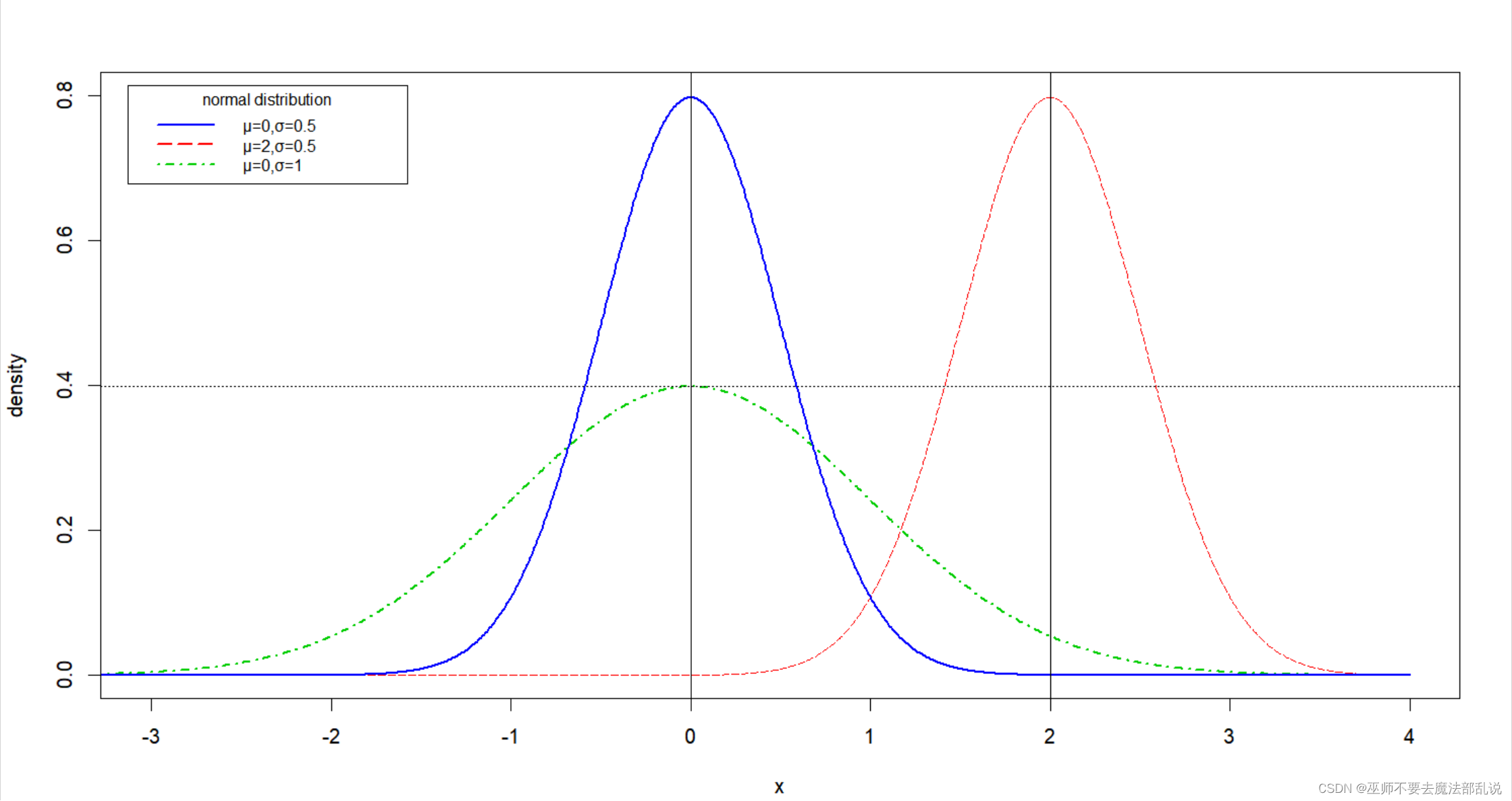
按照参考代码,在一个图中绘制如下图所示的三个正态分布的概率密度函数曲线。要求(第4-7题要求与此类似,不再重复说明):
(1)生成图形后,点击RStudio右下角区域中的“Plot”标签下的“Export”按钮,在弹出的菜单中选择“Save as Image…”,保存为PNG格式。然后将此PNG图片插入到此文档中,替换掉原来的样例图。
(2)删除参考代码截图,并粘贴代码文字到此文档中(不是截图)。
(3)对其中的一些参数,可以修改其值或者注释掉该参数,看看生成的图形有什么变化,从而加深理解这些参数的意义。
参考代码:
x <- seq(-4,4,length.out =1000)y1 <- dnorm(x)y2 <- dnorm(x,mean = 2,sd = 0.5)y3 <-dnorm(x,mean = 0,sd = 0.5)plot(x,y1,type = "l",lty =4,col ="green3",lwd = 2,xlim = c(-3,4),ylim = c(0,0.8),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n",)lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1,at = seq(-3,4,by = 1))axis(side = 2,at = seq(0,0.8,by = 0.2))abline(v = 0)abline(v = 2)abline(h = max(y1),lty = 3)legend("topleft",inset = 0.02,title = "normal distribution",c("μ=0,σ=0.5","μ=2,σ=0.5","μ=0,σ=1"),cex = 0.8,lty = c(1,5,4),lwd = 2,col = c("blue","red","green3"))在一个图中,绘制第3题中三个正态分布函数的累积分布函数曲线。(注意为了让曲线完整显示,纵轴的范围需要调整为0到1之间,同时将纵坐标的标签改为CDF,即累积分布函数(Cumulative Distribution Function))

替换以上样例图,并粘贴代码文字于下(非截图)
代码:
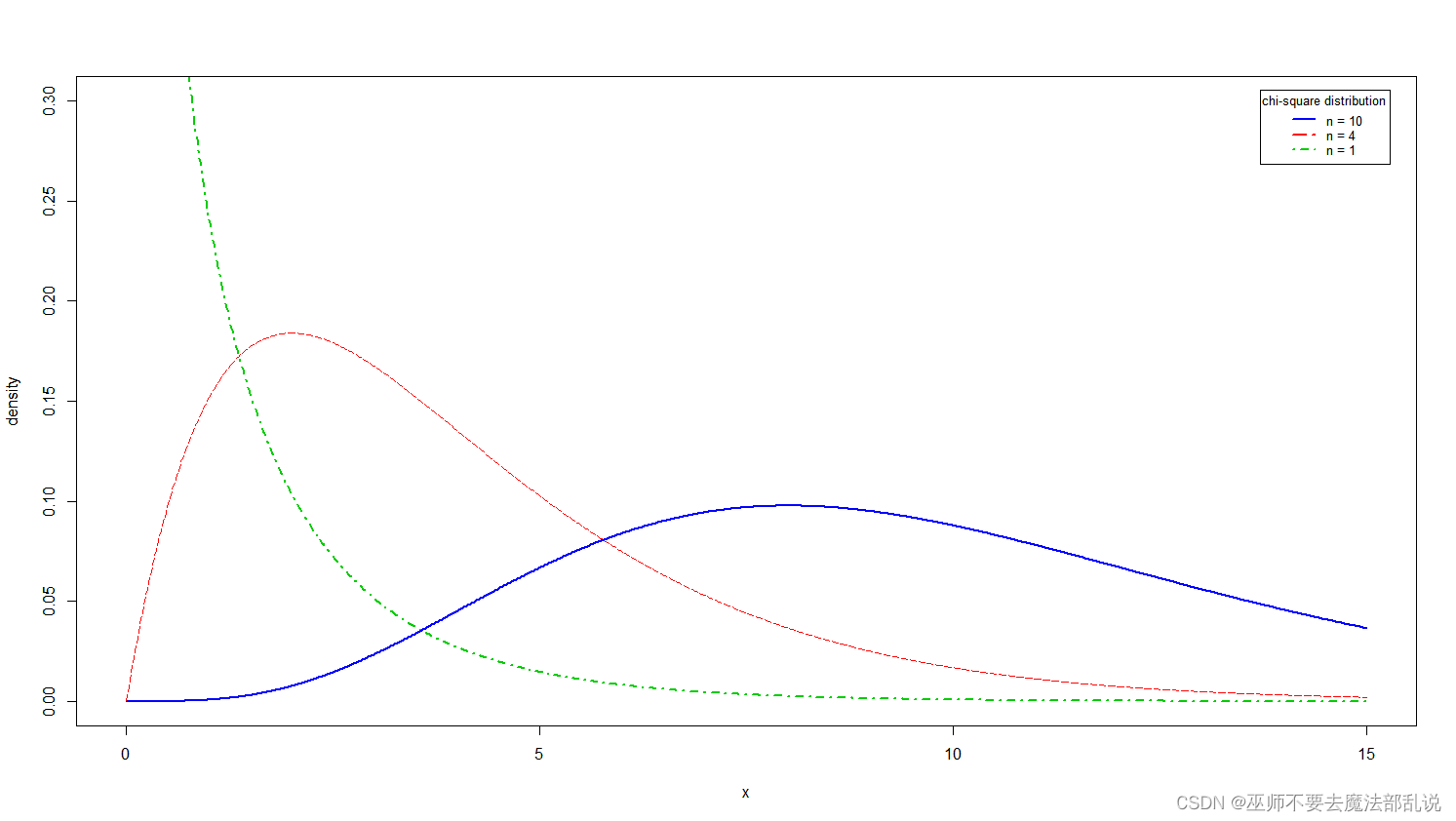
x <- seq(-4,4,length.out =1000)y1 <- pnorm(x)y2 <- pnorm(x,mean = 2,sd = 0.5)y3 <-pnorm(x,mean = 0,sd = 0.5)plot(x,y1,type = "l",lty =4,col ="green",lwd = 2,xlim = c(-4,4),ylim = c(0,1),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n",)lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1,at = seq(-4,4,by = 2))axis(side = 2,at = seq(0,1,by = 0.2))abline(v = 0)abline(v = 2)#abline(h = max(y1),lty = 3)legend("topleft",inset = 0.02,title = "累积密度函数曲线",c("μ=0,σ=0.5","μ=2,σ=0.5","μ=0,σ=1"),cex = 0.8,lty = c(1,5,4),lwd = 2,col = c("blue","red","green3"))模仿第3题,绘制下图所示的三个c2分布的概率密度函数曲线。(注意坐标轴刻度、图例等的变化)
替换以上样例图,并粘贴代码文字于下(非截图)
代码:
x <- seq(0,15, length.out = 1000)y1 <- dchisq(x, df = 1)y2 <- dchisq(x, df = 4)y3 <- dchisq(x, df = 10)plot(x,y1,type = "l",lty = 4,col = "green3",lwd = 2,xlim = c(0, 15),ylim = c(0.00, 0.30),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n")lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1, at = seq(0, 15, by = 5))axis(side = 2, at = seq(0, 0.30, by = 0.05))#abline(v = 0)#abline(v = 2)#abline(h = max(y1), lty = 3)legend("topright",inset = 0.02,title = "chi-square distribution",c("n = 10", "n = 4", "n = 1"),cex = 0.8,lty = c(1, 5, 4),lwd = 2,col = c("blue", "red", "green3"))模仿第3题,绘制下图所示的三个t分布的概率密度函数曲线。(注意坐标轴刻度、图例等的变化)

替换以上样例图,并粘贴代码文字于下(非截图)
代码:
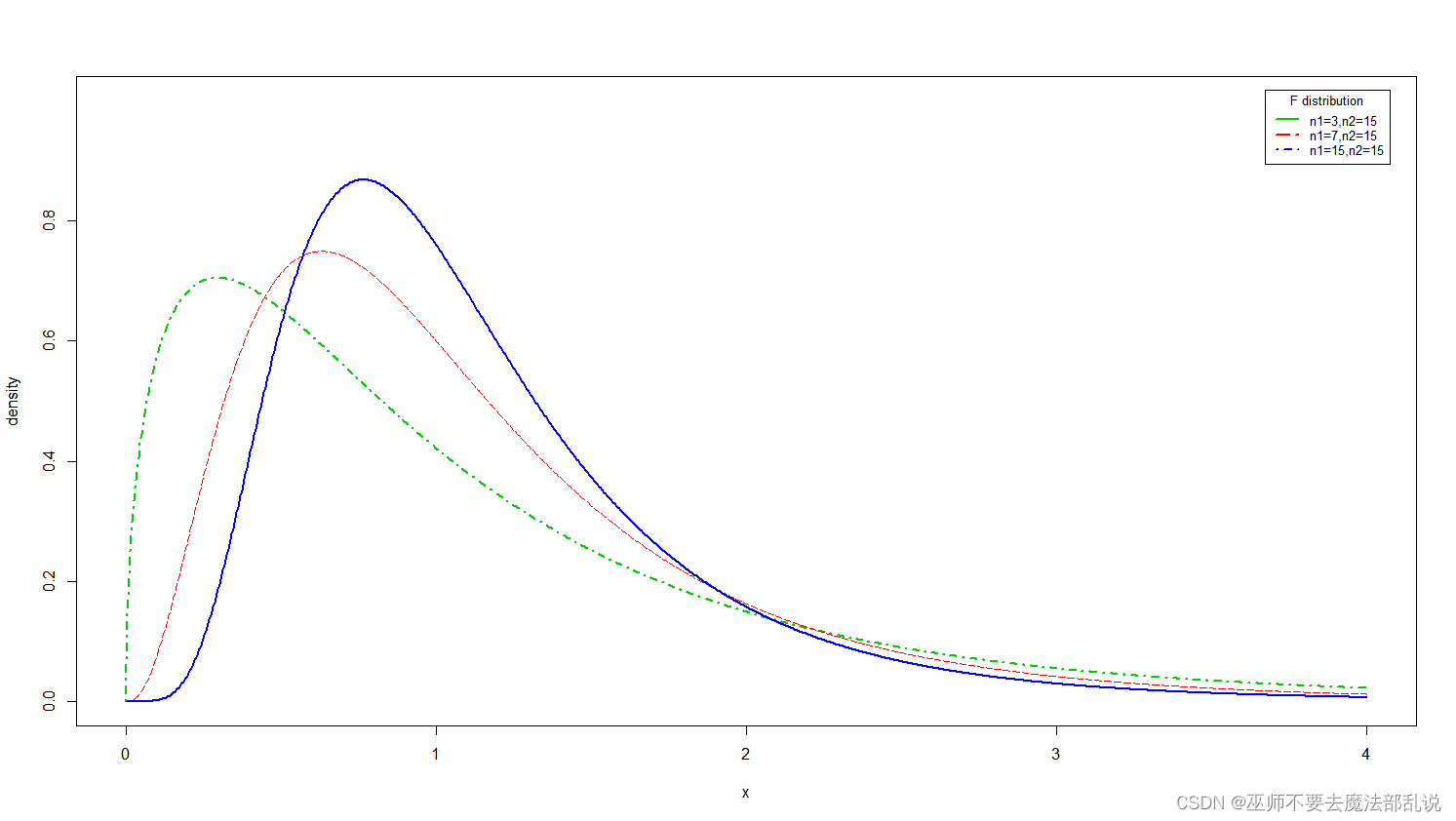
x <- seq(0,15, length.out = 1000)y1 <- dchisq(x, df = 1)y2 <- dchisq(x, df = 4)y3 <- dchisq(x, df = 10)plot(x,y1,type = "l",lty = 4,col = "green3",lwd = 2,xlim = c(0, 15),ylim = c(0.00, 0.30),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n")lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1, at = seq(0, 15, by = 5))axis(side = 2, at = seq(0, 0.30, by = 0.05))#abline(v = 0)#abline(v = 2)#abline(h = max(y1), lty = 3)legend("topright",inset = 0.02,title = "chi-square distribution",c("n = 10", "n = 4", "n = 1"),cex = 0.8,lty = c(1, 5, 4),lwd = 2,col = c("blue", "red", "green3"))模仿第3题,绘制下图所示的三个F分布的概率密度函数曲线。(注意坐标轴刻度、图例等的变化。图例中字符的下标不做要求)
替换以上样例图,并粘贴代码文字于下(非截图)
代码:
x <- seq(0,4, length.out = 1000)y1 <- df(x,3,15)y2 <- df(x,7,15)y3 <- df(x,15,15)plot(x,y1,type = "l",lty = 4,col = "green3",lwd = 2,xlim = c(0, 4),ylim = c(0.00, 1.0),xlab = "x",ylab = "density",xaxt = "n",yaxt = "n")lines(x,y2,lty = 5,col = "red")lines(x,y3,lty = 1,lwd = 2,col = "blue")axis(side = 1, at = seq(0, 4, by = 1))axis(side = 2, at = seq(0, 0.8, by = 0.2))#abline(v = 0)#abline(h = max(y1), lty = 3)legend("topright",inset = 0.02,title = "F distribution",c("n1=3,n2=15", "n1=7,n2=15","n1=15,n2=15"),cex = 0.8,lty = c(1, 5, 4),lwd = 2,col = c("green3", "red", "blue"))思考:
常见离散型随机变量的分布有哪些?
伯努利分布、二项分布、泊松分布、几何分布、超几何分布
常见连续型随机变量的分布有哪些?
正态分布、指数分布、均匀分布、伽马分布、卡方分布、t分布、F分布
二项分布适用于__有__放回的抽样,超几何分布适用于__无__放回的抽样。(填“有”或“无”)
描述某一特定时间段内或空间段内事件发生次数的随机变量,通常服从什么分布?
泊松分布
描述两个事件间隔时间长度的随机变量,通常服从什么分布?
指数分布
统计量是样本的函数,且不包含总体的未知参数,它是随机变量吗?
统计量是随机变量
常用的抽样方法有两大类:概率型抽样方法和非概率抽样方法。它们各自又含有哪些具体的方法?
概率型抽样方法包括简单随机抽样、分层抽样、整群抽样、多阶段抽样等;
非概率抽样方法包括方便抽样、判断抽样、整齐抽样、比例抽样等。
