当前位置：首页 > news >正文

机试：进制转换问题

news 2025/8/14 7:02:43

十进制转任意进制

简单回忆一下十进制我们是怎么转换成二进制的（短除法）：

我们会将十进制数不断的进行除2操作，并且记录下每一次的余数（这个余数就是我们最终求的二进制数的组成部分）。

以下以12D举例，将其转换成二进制数：

除2 被除数 ------------- 余数

2 / 1 2 --------------- 0 （=12%2）

商&下一个被除数 6 (=12/2) -------------- 0 （=6%2）

3 (=6/2) -------------- 1 (=3%2)

1 (=3/2) -------------- 1 (=1%2)

0 (=1/2,结束)

计算出的余数由下往上组合就是我们要求的二进制数，即 $12_{10}\rightarrow 1100_{2}$

那么我们就要把这个思路转换成相对应的计算机代码了。

我们仅仅需要一个循环就可以完成这件事：

//n是我们待转化的十进制数
int ans[100];//用于存放我们的计算结果
int len=0;//用于记录我们转换的二进制有多少位
while(n!=0){ans[len++]=n%2;//取余运算，将结果保存同时位数len加一n/=2;//记录下一个被除数
}
//输出我们的二进制时，别忘了要逆序输出（短除法）
for(int i=len-1;i>=0;i--){printf("%d",ans[i]);
}

现在我们把这个思路拓展到x进制的转换。

首先，在所有x小于10的x进制转换中，都可以沿用上面的这个思路，只需要更改%2和/2即可：

//n是我们待转化的十进制数,x代表我们要转化的是几进制
int ans[100];//用于存放我们的计算结果
int len=0;//用于记录我们转换的x进制有多少位
while(n!=0){ans[len++]=n%x;//取余运算，将结果保存同时位数len加一n/=x;//记录下一个被除数
}
//输出我们的x进制时，别忘了要逆序输出（短除法）
for(int i=len-1;i>=0;i--){printf("%d",ans[i]);
}

但对于x>10的进制转换，这样做显然不太可行，拿十六进制举例，大于9的数使用字母进行表示。

为了能够将十进制以上和以下进行统一，我们修改以下我们的代码。

注意：以下代码可以适用于所有十进制转任意进制的情况：

#include <stdio.h>
#include <stdlib.h>
#define MAX 30
int main(){int n;char ans[MAX];//更改结果类型，采用char保存结果int len;int x;//代表转成几进制scanf("%d",&x);while(scanf("%d",&n)!=EOF){len=0;while(n!=0){if(n%x<10)ans[len++]=n%x+'0';//小于10直接存数else ans[len++]=n%x-10+'A';//大于10存放字母n/=x;}for(int i=len-1;i>=0;i--){//结果逆序输出printf("%c",ans[i]);}printf("\n");}return 0;
}

任意进制转十进制

同样先来看二进制，我们采用的是乘法。

平时我们想把二进制转十进制很简单，直接按位计算相加就行：

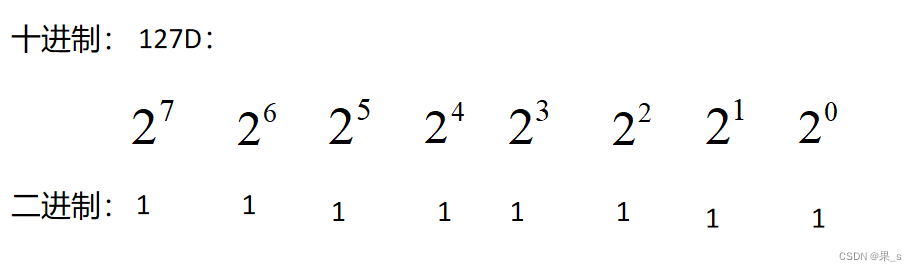
那么转换成代码我们又该怎么表示呢？

我们从最高位开始计算（）：

以下代码即为二进制的转换：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 30
int main(){char s[30];//代表二进制数int ans=0;//存储十进制答案scanf("%s",s);int len=strlen(s);for(int i=0;i<len;i++){ans*=2;ans+=s[i]-'0';}printf("%d\n",ans);return 0;
}

拓展到任意进制与上述方法类似，就不再赘述了，直接上代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX 30
int main(){char s[30];//代表二进制数int ans=0;//存储十进制答案int x;//用于记录转换为x进制scanf("%d",&x);int len;while(scanf("%s",s)!=EOF){len=strlen(s);ans=0;for(int i=0;i<len;i++){ans*=x;if(s[i]>='0'&&s[i]<='9')ans+=s[i]-'0';else ans+=s[i]-'A'+10;}printf("%d\n",ans);}return 0;
}

大数进制转换

思路来源：大数的进制转换_大数进制转换-CSDN博客

指路这位大佬。

题目描述：将一个长度最多为30位数字的十进制非负整数转换为二进制数输出

之前我们在进行十进制转二进制时，不断地在重复模2、除2的操作。但这对于大数来说并不好实现（因为之前我们使用一个整型存储数据，而现在我们使用字符串来存储大数）

大数除法

根据以上那位大佬的思路，我明白了每一次除法运算的内在流程。

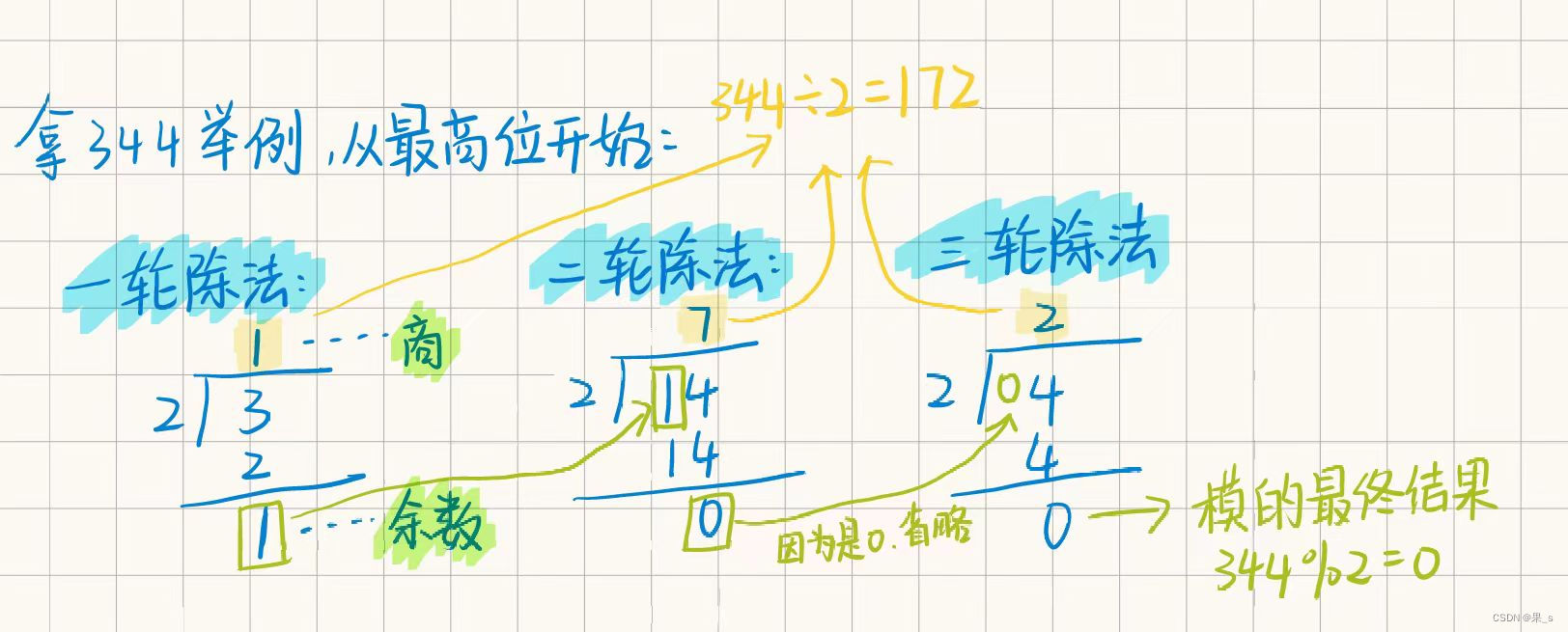
除法运算从被除数（344）的最高位开始，每一轮除法都取被除数的一位出来进行运算。

应该进行几轮除法由被除数（344）的位数决定，比如这里344一共有个十百三位，也就需要进行3轮除法。

在每一轮除法中，我们都会得到一个商和余数（回归到余数最本质的定义：剩余的、没有除完的数称为余数，因此在下一轮除法操作时要将上一轮的余数带上）。

所以现在基本上已经理清楚了，我们所要求的除法结果其实就是每一轮的商合在一起的结果。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>int main() {char x[1000];//我们的十进制待转换数char* tmp;//用于存储被除数int len = strlen(x);//用于保存被除数的长度//以下定义看名字应该也知道是什么，写的是拼音int yushu, shang,  beichushu;int count;//count用于记录下一轮被除数应得的长度char ans[1000];//用于记录二进制结果int ans_len;//代表二进制结果的位数while(scanf("%s", x)!=EOF){tmp=x;len=strlen(x);ans_len=0;//以下循环是计算一个完整的二进制数的过程while (len != 0)//当被除数不等于0的时候，就需要进行循环{count = 0;yushu = 0;shang = 0;//这个循环才是一轮除法的循环过程for (int i = 0; i < len; i++) {beichushu = yushu * 10 + tmp[i] - '0';yushu = beichushu % 2;shang = beichushu / 2;x[count++] = shang + '0';//记录下每一次运算的商}ans[ans_len++] = yushu + '0';//以下操作是将商前面多余的零删除掉，只留下有效位的操作int j = 0;while (x[j] == '0')j++;len=0;while (j < count) {tmp[len++] = x[j++];}}for (int i = ans_len - 1; i >= 0; i--) {printf("%c", ans[i]);}printf("\n");}return 0;}

查看全文

http://www.lryc.cn/news/342342.html