(双指针) 有效三角形的个数 和为s的两个数字 三数之和 四数之和
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
目录
文章目录
前言
一、有效三角形的个数(medium)
1.1、题目
1.2、讲解算法原理
1.3、编写代码
二、和为s的两个数字
2.1、题目
2.2、讲解算法原理
2.3、编写代码
三、三数之和
3.1、题目
3.2、讲解算法原理
3.3、编写代码
四、四数之和
4.1、题目
4.2、讲解算法原理
4.3、编写代码
总结
前言
世上有两种耀眼的光芒,一种是正在升起的太阳,一种是正在努力学习编程的你!一个爱学编程的人。各位看官,我衷心的希望这篇博客能对你们有所帮助,同时也希望各位看官能对我的文章给与点评,希望我们能够携手共同促进进步,在编程的道路上越走越远!
提示:以下是本篇文章正文内容,下面案例可供参考
一、有效三角形的个数(medium)
1.1、题目

1.2、讲解算法原理
补充数学知识:给我们三个数,判断是都能够构成三角形。

步骤:利用单调性,使用双指针算法来解决问题。
- 先固定最大的数;
- 在最大的数的左区间内,使用双指针算法,快速统计出符合要求的三元组的个数。
来举例一个区间[2,2,3,4,4,9,10]来说明一下情况:
- 优化:先对整个数组排序,用于固定最大的数。
- 我们根据三角形的满足条件得出的两个结论:因为数组是升序的,所以设a和b为最小的两边,c为最大的边,a + b > c就能构成三角形;a + b <= c便不能构成三角形。
- 我们使用双指针的思想,假设数组的下标为指针,设left指针指向数组下标为0的位置,设right指针指向数组中最大的数的左区间中的最大值。
- 拿上面的数组为例,先固定最大的数为10,设left为第一个2所在的位置,right为9所在的位置,left + right大于10,因为是升序,所以当right不变,left指向2~9之间的任意数时,都符合三角形的条件,因此得出的结论:下标right - left的值为满足三角形的情况,9所在的位置可以划掉,right--。
- 此时left为第一个2,right为5,最大值依旧为10:2 + 5 < 10,不构成三角形的条件,left++,再次判断三角形的条件,重复操作,直到left和right相遇,最大值为10所在的情况查看完毕,更新最大值。
1.3、编写代码
class Solution
{
public:int triangleNumber(vector<int>& nums) {// 先进行排序sort(nums.begin(), nums.end());// 利用双指针解决问题int ret = 0, n = nums.size();for(int i = n-1; i>= 2; i--)// 固定最大值{int left = 0,right = i - 1;while(left < right){if(nums[left] + nums[right] > nums[i]){ret += (right - left);right--;}else{left++;}}}return ret;}
};
二、和为s的两个数字
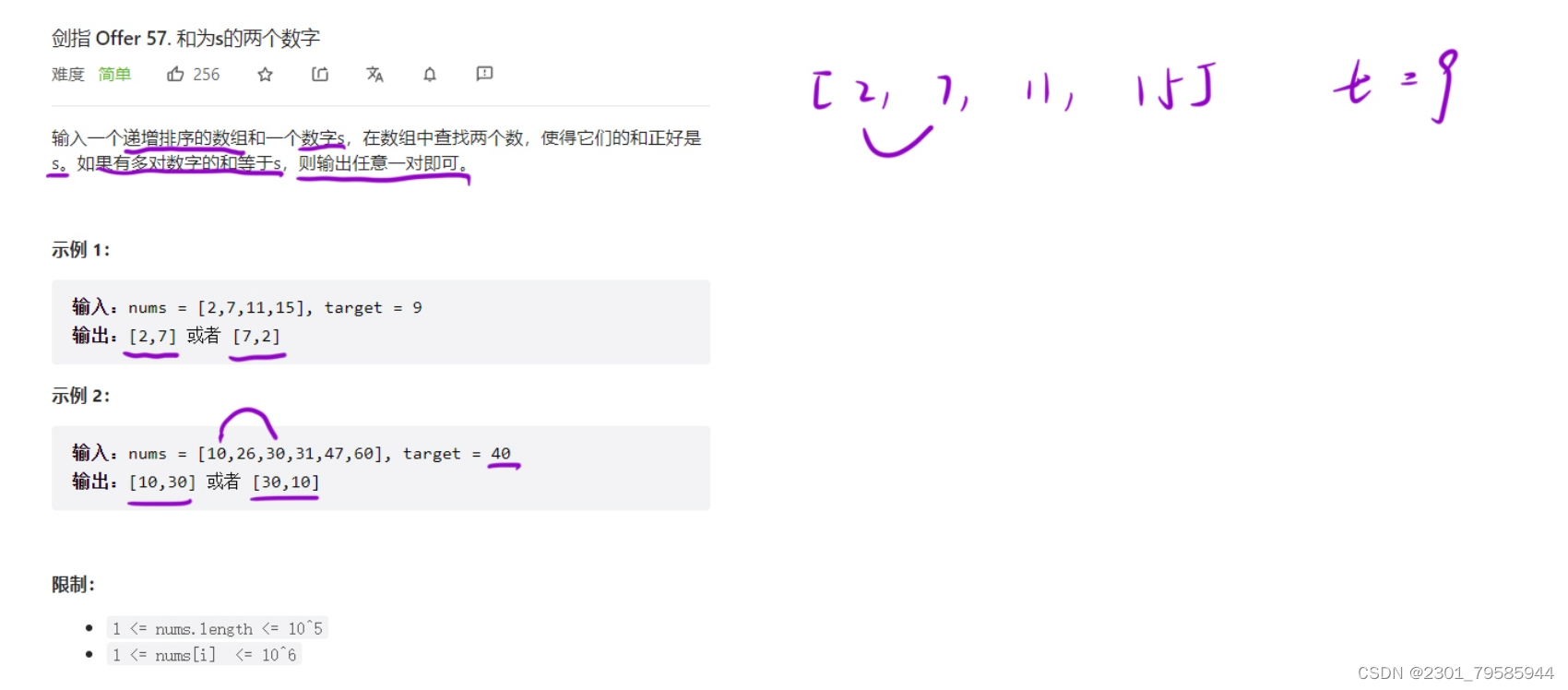
2.1、题目
2.2、讲解算法原理
利用单调性,使用双指针算法解决问题。
举一个数组[2,7,11,15,19,21],t = 30为例:设left指针指向2,right指针指向21,让两数相加来和t值(30)比较。
分为三种情况:
- sum < t:left为2,right为21,相加得23 < t(30),因为数组为递增顺序,left和right区间的数字都比21要小,因此划掉2,left++;
- sum > t:left为11,right为21,相加得32 > t(30),left和right区间的数值都比left(11)要大,因此划掉21,right--;
- sum = t(30):返回结果。
2.3、编写代码
class Solution
{
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0,right = price.size() - 1;while(left < right){if(price[left] + price[right] > target){right--;}else if(price[left] + price[right] < target){left++;}else{return {price[left],price[right]};}}// 照顾编译器return {-1,-1};}
};
三、三数之和
3.1、题目


3.2、讲解算法原理

步骤:
- 排序;
- 固定一个数a;(小优化:对于下面的数组来说,a > 0之后,不管left 和 right 两个指针指向哪里,和 a 相加之后,都不会等于0,因此 a > 0之后,就可以结束了)
- 在该固定的数a后面的区间内,利用“双指针算法”快速找到两个的和等于 -a 即可。
处理细节问题:
1、去重;
- 找到一种结果之后,left 和 right 指针要跳过重复元素;
- 当使用完一次双指针算法之后,i 也需要跳过重复的元素;
- 避免越界。
2、不漏;
- 找到一种结果之后,不要“停”,缩小区间,继续寻找。

3.3、编写代码
class Solution
{
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> ret;// 定义一个二级数组用于储存数组// 排序sort(nums.begin(), nums.end());int i = 0, n = nums.size();// 固定一个数afor(i = 0; i < n; ) // for()循环中初始化、判断和调整这三个部分都可以写为空{// 小优化if(nums[i] > 0) break;int left = i + 1, right = n - 1, target = -nums[i];// target两个指针所指向的数相加==固定数的负数while(left < right){int sum = nums[left] + nums[right];if(sum > target) right--;else if(sum < target) left++;else {ret.push_back({nums[i], nums[left], nums[right]});left++, right--;// 去重操作 left rightwhile(left < right && nums[left] == nums[left - 1]) left++;while(left < right && nums[right] == nums[right + 1]) right--;}}i++;// 去重操作 iwhile(i < n && nums[i] == nums[i - 1]) i++;}return ret;}
};
四、四数之和
4.1、题目


4.2、讲解算法原理
排序 + 双指针:
- 依次固定一个数a;
- 在 a 后面的区间内,利用"三数之和"找到三个数,使这三个数的和等于 target -a 即可。
三数之和:
- 依次固定一个数 b;
- 在 b 后面的区间内,利用"双指针"找到两个数,使这两个数的和等于 target - a - b 即可。
处理细节问题:
1、去重;
- 找到一种结果之后,left 和 right 指针要跳过重复元素;
- 当使用完一次双指针算法之后,i 也需要跳过重复的元素;
- 避免越界。
2、不漏;
- 找到一种结果之后,不要“停”,缩小区间,继续寻找。

4.3、编写代码
class Solution
{
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {// 定义一个二级数组,用来存放数组vector<vector<int>> ret;// 排序sort(nums.begin(),nums.end());// 固定一个数aint i = 0,n = nums.size();for(i = 0; i < n; ){// 固定数b ---> 将四数求和转换成三数求和for(int j = i + 1; j < n; ){// 利用双指针的算法int left = j + 1, right = n -1; while(left < right){// 这个地方用int类型,有可能会超出int的范围,用long longlong long aim = (long long)target - nums[i] - nums[j];int sum = nums[left] + nums[right];if(sum > aim) right--;else if(sum < aim) left++;else{ret.push_back({nums[i], nums[j], nums[left], nums[right]});left++, right--;// 去重操作 left rightwhile(left < right && nums[left] == nums[left-1]) left++;while(left < right && nums[right] == nums[right+1]) right--;}}j++;// 去重操作 jwhile(j < n && nums[j] == nums[j-1]) j++;}i++;// 去重操作 iwhile(i < n && nums[i] == nums[i-1]) i++;}return ret;}
};
总结
好了,本篇博客到这里就结束了,如果有更好的观点,请及时留言,我会认真观看并学习。
不积硅步,无以至千里;不积小流,无以成江海。
