力扣每日一题114:二叉树展开为链表
题目
中等
提示
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
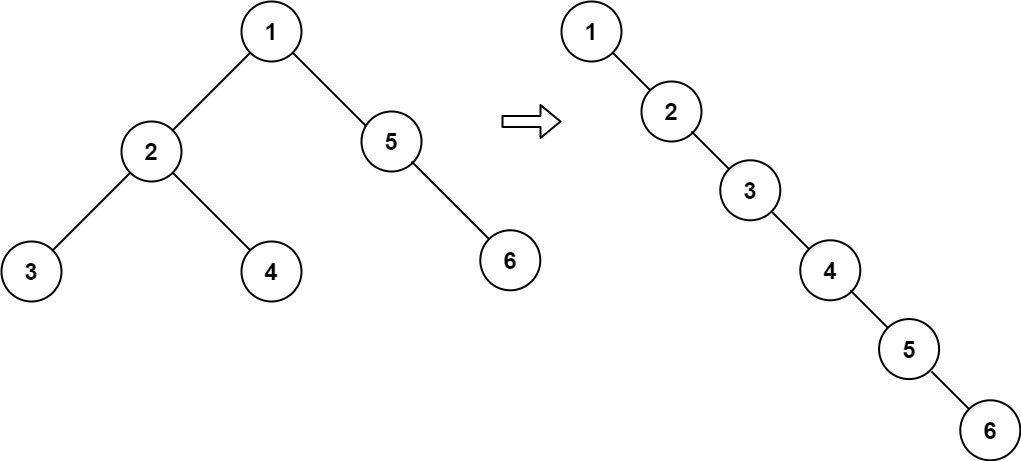
输入:root = [1,2,5,3,4,null,6] 输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [0] 输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
进阶:你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
面试中遇到过这道题?
1/5
是
否
通过次数
465.3K
提交次数
631.8K
通过率
73.6%
结点结构
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/方法一:前序遍历
前序遍历所有的结点,将遍历的结点依次放入一个数组中,然后再转换成单链表。
class Solution {
public:void preorder(TreeNode *root,vector<TreeNode*> &temp){if(!root) return ;temp.push_back(root);preorder(root->left,temp);preorder(root->right,temp);}void flatten(TreeNode* root) {if(!root) return;vector<TreeNode*> temp;preorder(root,temp);temp.push_back(NULL);for(int i=0;i<temp.size()-1;i++){temp[i]->left=NULL;temp[i]->right=temp[i+1];}}
};官解还提供了下面两种方法
方法二:前序遍历和展开同时进行
使用方法一的前序遍历,由于将节点展开之后会破坏二叉树的结构而丢失子节点的信息,因此前序遍历和展开为单链表分成了两步。能不能在不丢失子节点的信息的情况下,将前序遍历和展开为单链表同时进行?
之所以会在破坏二叉树的结构之后丢失子节点的信息,是因为在对左子树进行遍历时,没有存储右子节点的信息,在遍历完左子树之后才获得右子节点的信息。只要对前序遍历进行修改,在遍历左子树之前就获得左右子节点的信息,并存入栈内,子节点的信息就不会丢失,就可以将前序遍历和展开为单链表同时进行。
该做法不适用于递归实现的前序遍历,只适用于迭代实现的前序遍历。修改后的前序遍历的具体做法是,每次从栈内弹出一个节点作为当前访问的节点,获得该节点的子节点,如果子节点不为空,则依次将右子节点和左子节点压入栈内(注意入栈顺序)。
展开为单链表的做法是,维护上一个访问的节点 prev,每次访问一个节点时,令当前访问的节点为 curr,将 prev 的左子节点设为 null 以及将 prev 的右子节点设为 curr,然后将 curr 赋值给 prev,进入下一个节点的访问,直到遍历结束。需要注意的是,初始时 prev 为 null,只有在 prev 不为 null 时才能对 prev 的左右子节点进行更新。
class Solution {
public:void flatten(TreeNode* root) {if (root == nullptr) {return;}auto stk = stack<TreeNode*>();stk.push(root);TreeNode *prev = nullptr;while (!stk.empty()) {TreeNode *curr = stk.top(); stk.pop();if (prev != nullptr) {prev->left = nullptr;prev->right = curr;}TreeNode *left = curr->left, *right = curr->right;if (right != nullptr) {stk.push(right);}if (left != nullptr) {stk.push(left);}prev = curr;}}
};方法三:寻找前驱结点。(类似于Morris遍历)
前两种方法都借助前序遍历,前序遍历过程中需要使用栈存储节点。有没有空间复杂度是 O(1)O(1)O(1) 的做法呢?
注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。如果一个节点的左子节点为空,则该节点不需要进行展开操作。如果一个节点的左子节点不为空,则该节点的左子树中的最后一个节点被访问之后,该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点,也是该节点的前驱节点。因此,问题转化成寻找当前节点的前驱节点。
具体做法是,对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束。
class Solution {
public:void flatten(TreeNode* root) {TreeNode *curr = root;while (curr != nullptr) {if (curr->left != nullptr) {auto next = curr->left;auto predecessor = next;while (predecessor->right != nullptr) {predecessor = predecessor->right;}predecessor->right = curr->right;curr->left = nullptr;curr->right = next;}curr = curr->right;}}
};