day34|343. 整数拆分、96.不同的二叉搜索树
343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
问题分析:
1、确定dp[i]数组以及下标的含义
dp[i]:拆解i,得到的最大乘积dp[i]
2、确定递推公式
有两种方式获得dp[i]
- j * ( i - j )(拆分i,拆成2份)
- j * dp[ i - j ]( 让i - j继续拆分,拆成3份及3份以上)
求最大乘积:dp[i]=Math.max(Math.max(j*(i-j),j*dp[i-j]),dp[i]);
最后max里加dp[i],因为是求整个dp[i]的最大值
3、dp数组初始化
n从2开始,所以dp[2]=1+1,1*1=1
4、确定遍历顺序
dp[i]依靠dp[i-j]的状态,所以从前往后
5、打印dp数组
class Solution {public int integerBreak(int n) {int[] dp=new int[n+1];dp[2]=1;for (int i=3;i<=n;i++){for (int j=1;j<i;j++){dp[i]=Math.max(Math.max(j*(i-j),j*dp[i-j]),dp[i]);}}return dp[n];}
}96.不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
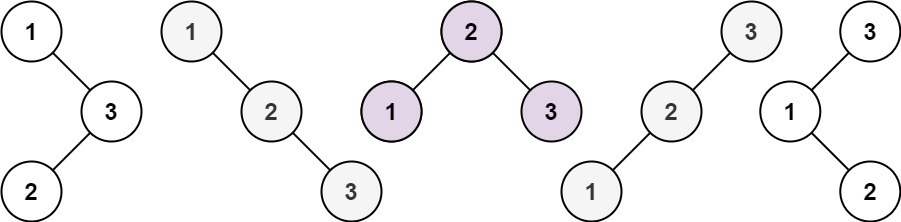
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
问题分析:
1、确定dp[i]数组以及下标的含义
dp[i]:1-i个节点组成的二叉搜索树的个数
2、确定递推公式
n=3:
1为头节点时,右子树有两个节点,布局和n=2时两棵树的布局一样(不关心数值,只关心布局)
2为头节点时,左子树有一个节点,右子树有一个节点,布局和n=1时一样
3为头节点时,左子树有两个节点,布局和n=2时两棵树的布局一样
dp[3]就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
递推公式:
dp[i]=dp[i]+dp[j]*dp[i-j-1]
j为左子树的节点数,i-j-1为右子树的节点数
3、dp数组初始化
dp[0]=1(空子树也为二叉搜索树),dp[1]=1
4、确定遍历顺序
dp[i]依靠dp[i-j-1]的状态,所以从前往后
5、打印dp数组
class Solution {public int numTrees(int n) {int[] dp = new int[n + 1];dp[0] = 1;//空节点也算二叉搜索树dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 0; j < i; j++) {dp[i] = dp[i] + dp[j] * dp[i - j - 1];}}return dp[n];}}
