代码随想录【Day15】|102. 二叉树的层序遍历、226. 翻转二叉树、101. 对称二叉树
102. 二叉树的层序遍历
题目链接
题目描述:
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。

难点:
思路:
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历BFS
时间复杂度:O()
空间复杂度:O()
//层序遍历
class Solution {List<List<Integer>> resList = new ArrayList<>(); //全局变量保存结果public List<List<Integer>> levelOrder(TreeNode root) {levelorder(root);return resList;}public void levelorder(TreeNode root) {if (root == null) return;Queue<TreeNode> que = new LinkedList<>();que.add(root);while (!que.isEmpty()) {int len = que.size(); //记录当前层的结点数List<Integer> itemList = new ArrayList<>();for (int i = 0; i < len; i++) {TreeNode cur = que.poll();itemList.add(cur.val);if (cur.left != null) que.offer(cur.left);if (cur.right != null) que.offer(cur.right);}resList.add(itemList);}}
}//DFS-递归法
class Solution {List<List<Integer>> resList = new ArrayList<>();public List<List<Integer>> levelOrder(TreeNode root) {int depth = 0;order(root, depth);return resList;}public void order(TreeNode root, int depth) {if (root == null) return;if (resList.size() == depth) resList.add(new ArrayList<>()); //仅当第一次遍历当该层(结果集的列表数等于当前深度)//创捷该层的结果队列resList.get(depth).add(root.val);order(root.left, depth+1);order(root.right, depth+1);}
}
时长:
20min
收获:
List是有get()和set()方法的!
层序遍历递归法
学会二叉树的层序遍历,可以一口气打完以下十题:
102.二叉树的层序遍历
107.二叉树的层次遍历II
199.二叉树的右视图
637.二叉树的层平均值
429.N叉树的层序遍历
515.在每个树行中找最大值
116.填充每个节点的下一个右侧节点指针
117.填充每个节点的下一个右侧节点指针II
104.二叉树的最大深度
111.二叉树的最小深度
226. 翻转二叉树
题目链接
题目描述:
翻转一棵二叉树。
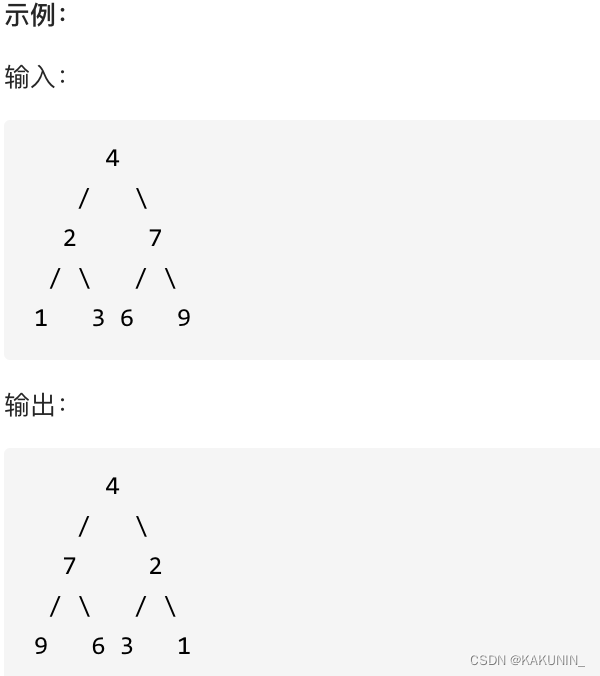
难点:
思路:
递归法,采用后序遍历或者先序遍历都可以
时间复杂度:O()
空间复杂度:O()
class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) return root;invertTree(root.left);invertTree(root.right);swap(root);return root;}public void swap(TreeNode root) {TreeNode tmp = root.left;root.left = root.right;root.right = tmp;}
}
另外还有迭代法、层序遍历法
时长:
10min
收获:
交换要拿到root,交换其左右节点
101. 对称二叉树
题目链接
题目描述:
给定一个二叉树,检查它是否是镜像对称的。

难点:
思路:
要判断对称,那就要以中轴线为划分,比较左右两边对应位置的内侧结点和外侧节点
先判断结点是否都存在
再判断结点的值是否相同
时间复杂度:O()
空间复杂度:O()
public boolean isSymmetric(TreeNode root) {if (root == null) return true;return compare(root.left, root.right);}private boolean compare(TreeNode left, TreeNode right) {if(left == null && right == null) {return true;}else if (left != null && right == null) {return false;}else if (left == null && right != null) {return false;}else if (left.val != right.val) {return false;}return compare(left.left, right.right) && compare(left.right, right.left);}
时长:
10min
收获:
仔细完整地考虑不同情况
