当前位置：首页 > news >正文

《算法导论》第 34 章 - NP 完全性

news 2025/8/21 10:15:10

大家好！今天我们深入拆解《算法导论》第 34 章 ——NP 完全性。这一章是算法复杂度分析的 “分水岭”：它帮我们区分 “能高效解决的问题” 和 “理论上难解的问题”，避免在工程中陷入 “为无解问题找解法” 的误区。

34.1 多项式时间

核心概念

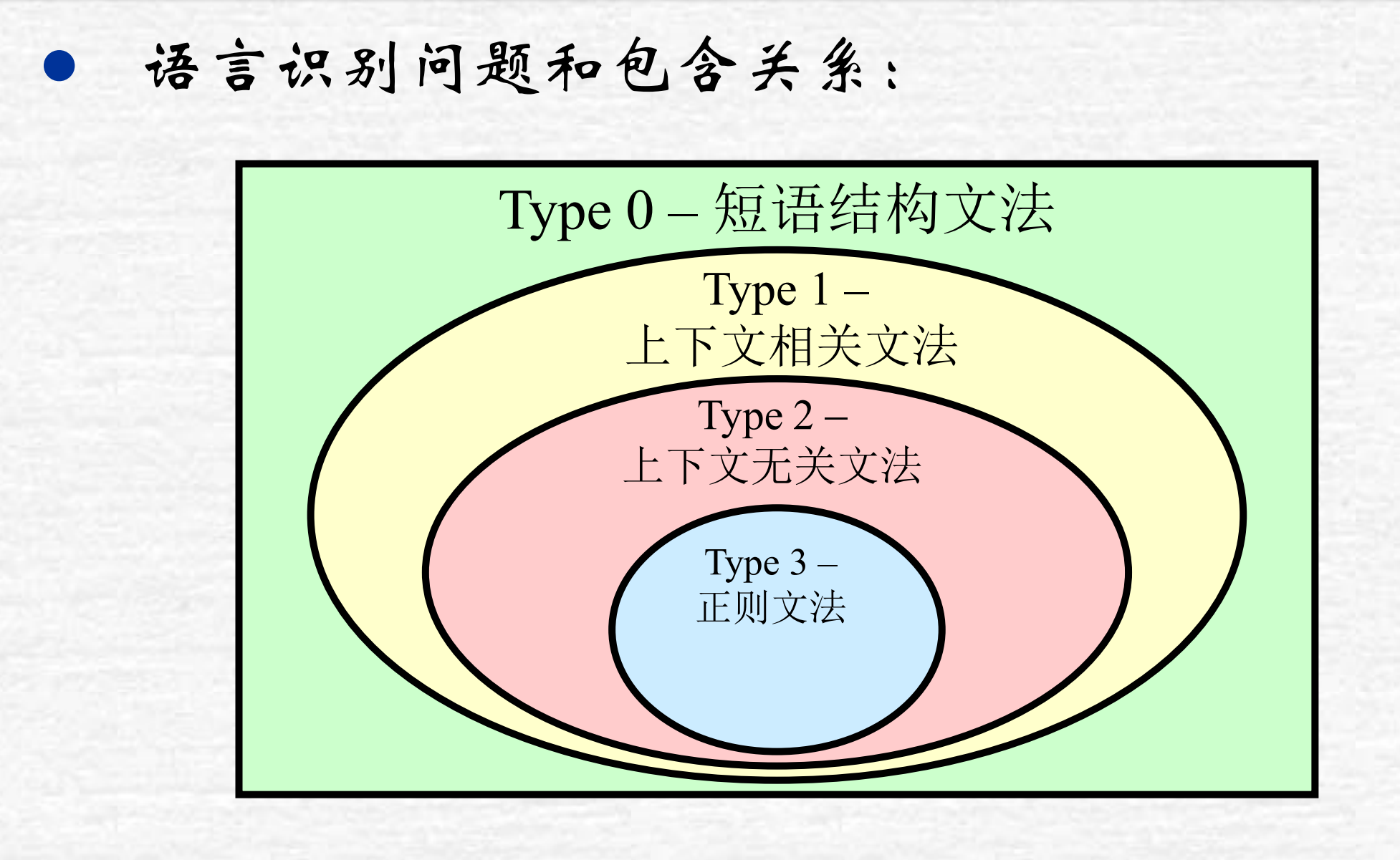
多项式时间是判断 “问题是否可高效解决” 的关键标准，基于确定性图灵机（DTM） 模型：

若算法的时间复杂度为 O(nᵏ)（n 是输入规模，k 是常数），则称其为多项式时间算法；
反之，O (2ⁿ)、O (n!) 等称为指数时间算法（输入稍大就无法运行）。

常见多项式时间复杂度：O (1) < O (logn) < O (n) < O (nlogn) < O (n²) < O (n³)。

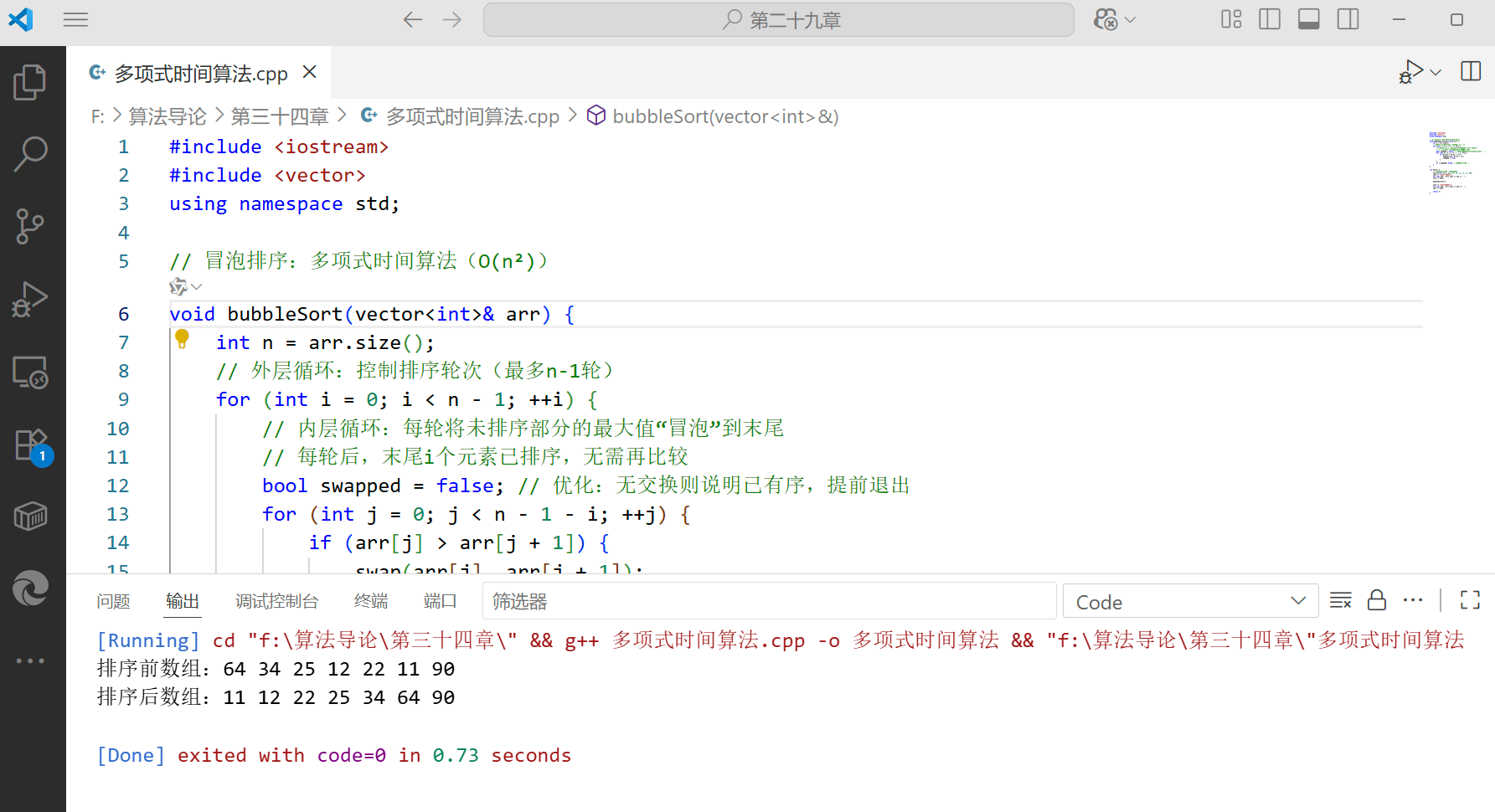
案例：多项式时间算法（冒泡排序）

冒泡排序的时间复杂度是 O (n²)，属于多项式时间。下面是完整可运行的 C++ 代码，用于排序整数数组：

#include <iostream>
#include <vector>
using namespace std;// 冒泡排序：多项式时间算法（O(n²)）
void bubbleSort(vector<int>& arr) {int n = arr.size();// 外层循环：控制排序轮次（最多n-1轮）for (int i = 0; i < n - 1; ++i) {// 内层循环：每轮将未排序部分的最大值“冒泡”到末尾// 每轮后，末尾i个元素已排序，无需再比较bool swapped = false; // 优化：无交换则说明已有序，提前退出for (int j = 0; j < n - 1 - i; ++j) {if (arr[j] > arr[j + 1]) {swap(arr[j], arr[j + 1]);swapped = true;}}if (!swapped) break; // 无交换，直接退出}
}int main() {// 测试案例：输入一个无序数组vector<int> arr = {64, 34, 25, 12, 22, 11, 90};cout << "排序前数组：";for (int num : arr) cout << num << " ";cout << endl;bubbleSort(arr);cout << "排序后数组：";for (int num : arr) cout << num << " ";cout << endl;return 0;
}

代码说明

输入：无序整数数组（示例为{64,34,...90}）；
逻辑：每轮通过相邻元素交换，将最大值移到末尾，未排序部分逐渐缩小；
优化：若某轮无交换，说明数组已有序，直接退出（减少不必要计算）；
编译运行：直接复制到 IDE（如 Dev-C++、VS），编译后即可执行，输出排序结果。

34.2 多项式时间的验证

核心概念：P 问题 vs NP 问题

这是 NP 完全性的基础，必须先理清两个概念：

问题类别	定义	例子
P 问题	能在多项式时间内解决的问题	冒泡排序（排序）、Dijkstra 算法（最短路径）
NP 问题	能在多项式时间内验证解的正确性的问题（不一定能高效解决，但解能快速验证）	哈密顿回路（给一个回路，验证是否经过所有顶点）

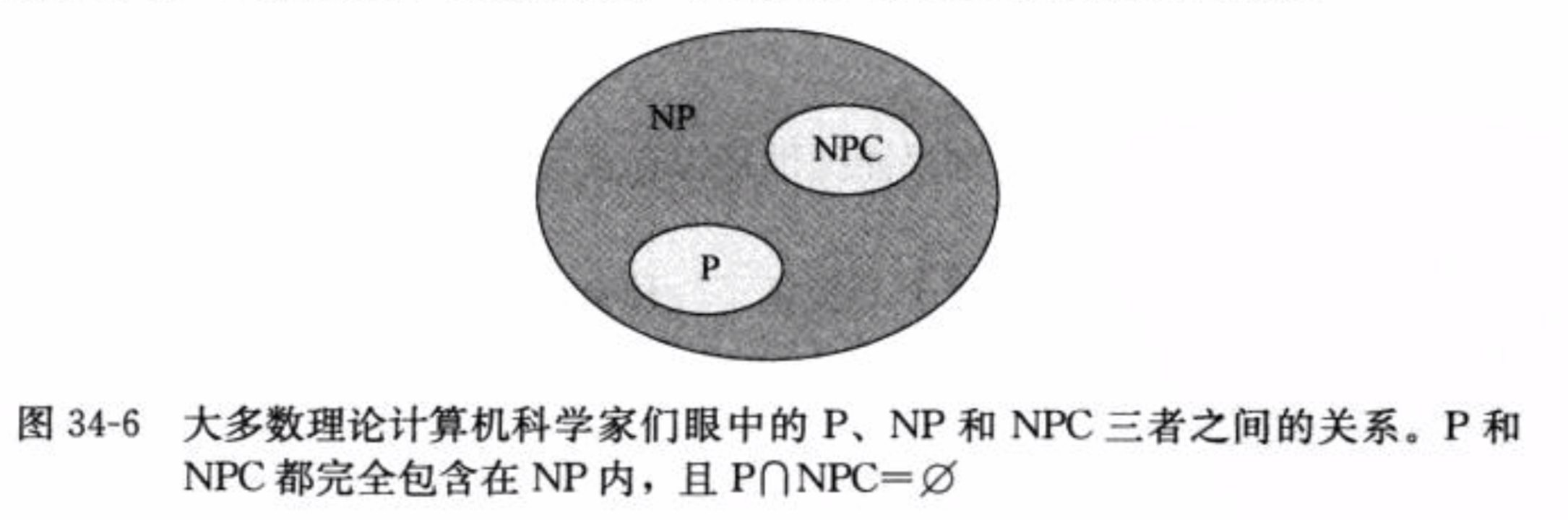
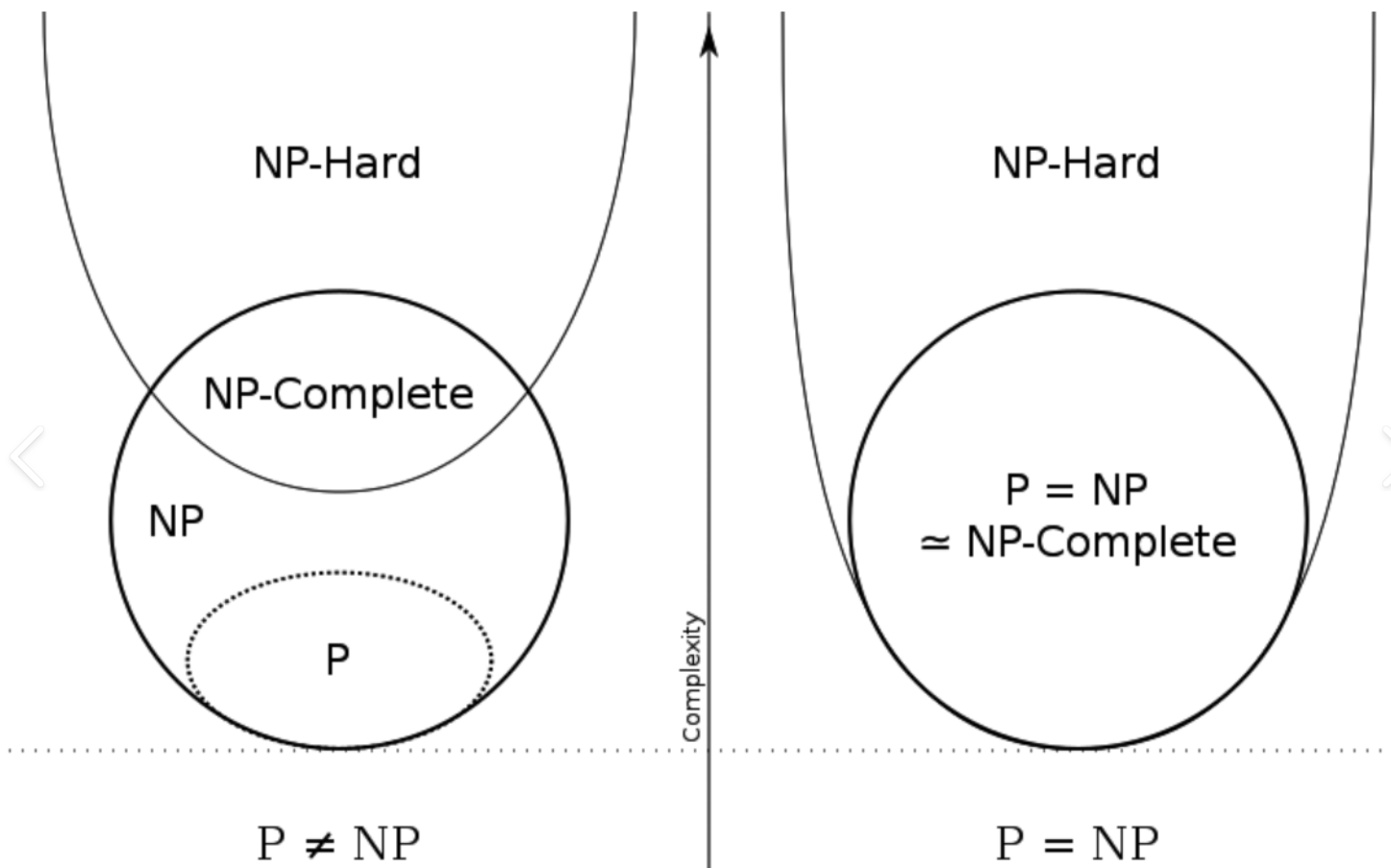
关键疑问：P 是否等于 NP？目前计算机科学未解决，但普遍猜想 P ≠ NP（即存在 NP 问题无法用多项式时间解决）。

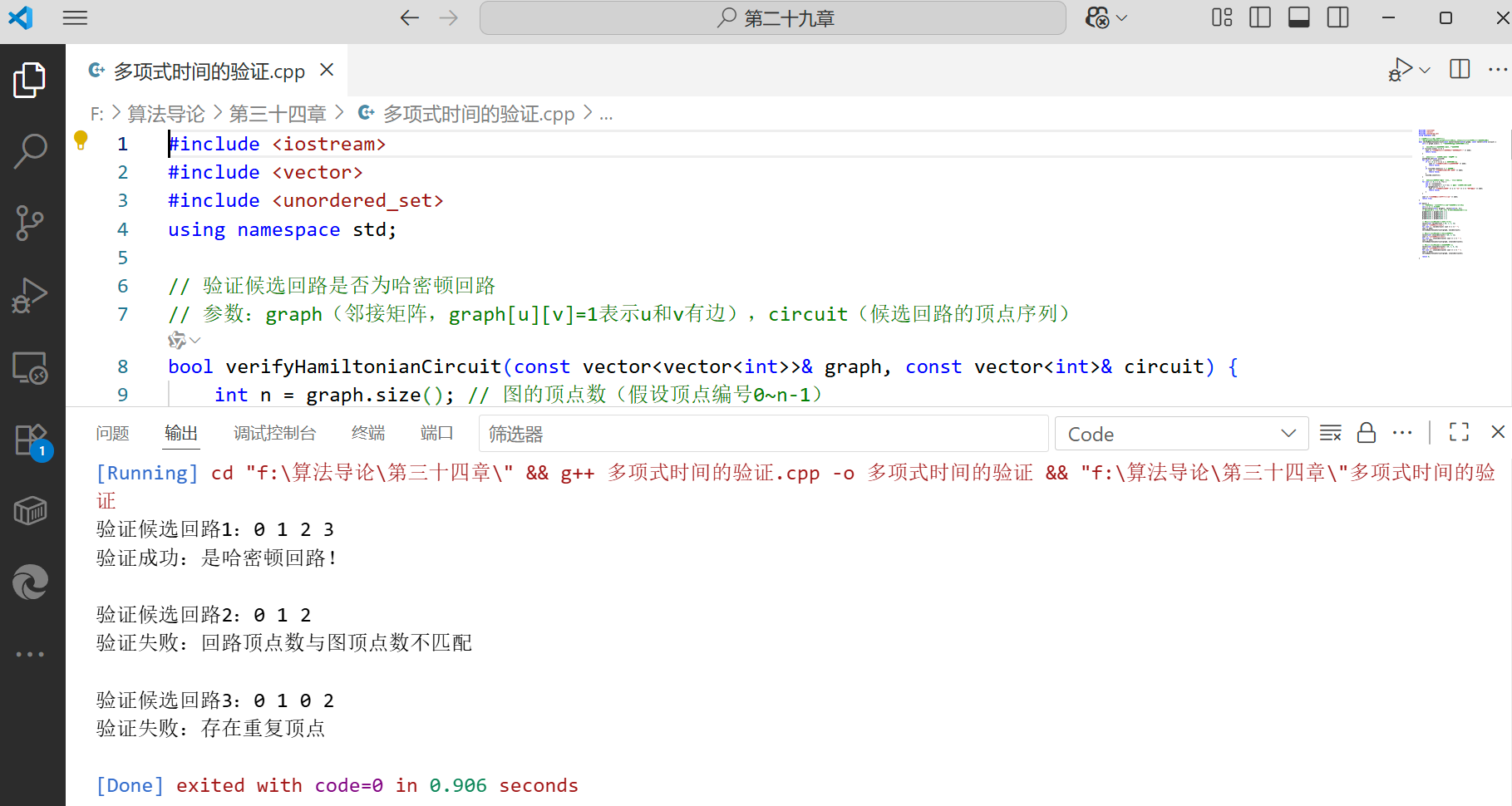
案例：哈密顿回路的验证算法

哈密顿回路（HC）的定义：给定无向图 G，是否存在一条经过所有顶点恰好一次，最后回到起点的回路。
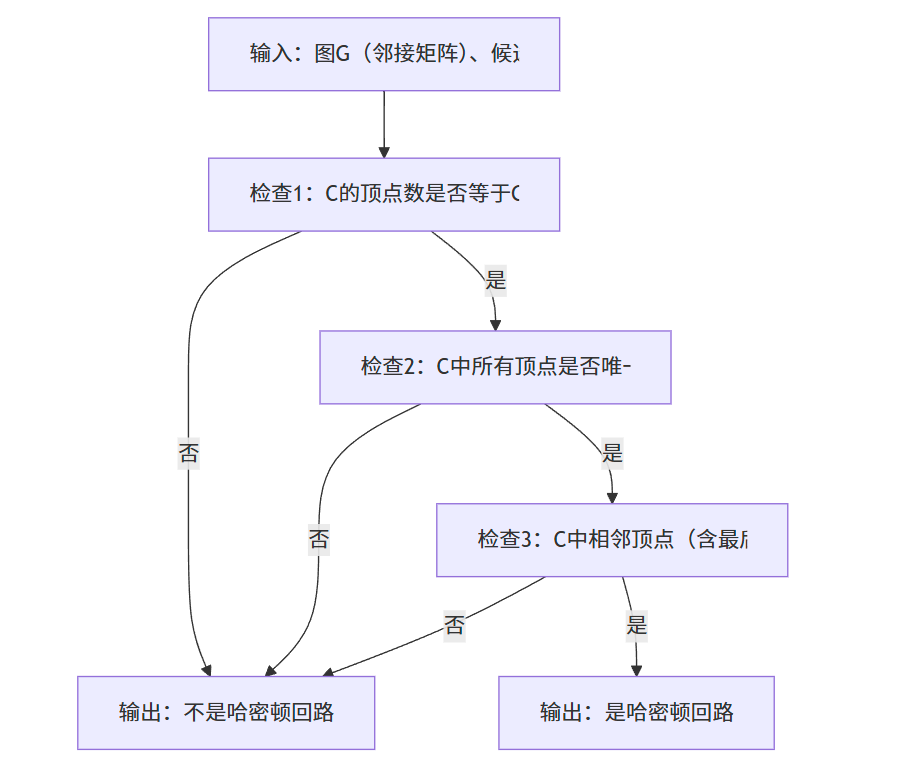
验证 HC 的解很简单：只需检查 “候选回路” 是否满足 3 个条件（多项式时间内完成）。

验证流程

完整 C++ 验证代码

#include <iostream>
#include <vector>
#include <unordered_set>
using namespace std;// 验证候选回路是否为哈密顿回路
// 参数：graph（邻接矩阵，graph[u][v]=1表示u和v有边），circuit（候选回路的顶点序列）
bool verifyHamiltonianCircuit(const vector<vector<int>>& graph, const vector<int>& circuit) {int n = graph.size(); // 图的顶点数（假设顶点编号0~n-1）// 检查1：候选回路的顶点数是否等于图的顶点数if (circuit.size() != n) {cout << "验证失败：回路顶点数与图顶点数不匹配" << endl;return false;}// 检查2：回路中所有顶点是否唯一（无重复）unordered_set<int> visited;for (int v : circuit) {if (v < 0 || v >= n) { // 顶点编号非法cout << "验证失败：存在非法顶点编号" << endl;return false;}if (visited.count(v)) { // 顶点重复cout << "验证失败：存在重复顶点" << endl;return false;}visited.insert(v);}// 检查3：相邻顶点（含最后一个与第一个）是否有边for (int i = 0; i < n; ++i) {int u = circuit[i];int v = circuit[(i + 1) % n]; // 最后一个顶点连接回起点if (graph[u][v] != 1) {cout << "验证失败：顶点" << u << "与" << v << "之间无边" << endl;return false;}}cout << "验证成功：是哈密顿回路！" << endl;return true;
}int main() {// 测试案例：一个有哈密顿回路的图（顶点0-1-2-3-0）int n = 4; // 4个顶点vector<vector<int>> graph(n, vector<int>(n, 0));// 构建边：0-1, 1-2, 2-3, 3-0, 0-2（额外边不影响回路）graph[0][1] = graph[1][0] = 1;graph[1][2] = graph[2][1] = 1;graph[2][3] = graph[3][2] = 1;graph[3][0] = graph[0][3] = 1;graph[0][2] = graph[2][0] = 1;// 候选回路1：正确的回路（0-1-2-3）vector<int> validCircuit = {0, 1, 2, 3};cout << "验证候选回路1：";for (int v : validCircuit) cout << v << " ";cout << endl;verifyHamiltonianCircuit(graph, validCircuit);// 候选回路2：错误的回路（缺少顶点3）vector<int> invalidCircuit1 = {0, 1, 2};cout << "\n验证候选回路2：";for (int v : invalidCircuit1) cout << v << " ";cout << endl;verifyHamiltonianCircuit(graph, invalidCircuit1);// 候选回路3：错误的回路（顶点0重复）vector<int> invalidCircuit2 = {0, 1, 0, 2};cout << "\n验证候选回路3：";for (int v : invalidCircuit2) cout << v << " ";cout << endl;verifyHamiltonianCircuit(graph, invalidCircuit2);return 0;
}

代码说明

图用邻接矩阵表示（graph[u][v] = 1表示边存在）；
验证逻辑严格遵循流程图：顶点数匹配→顶点唯一→边存在；
测试案例包含 1 个正确回路和 2 个错误回路，可直观看到验证结果。

34.3 NP 完全性与可归约性

核心概念

1. 多项式时间归约（≤ₚ）

若存在一个多项式时间算法，能将问题 A 的所有实例转化为问题 B 的实例，且 A 的解等价于 B 的解，则称A 可多项式时间归约到 B（记为 A ≤ₚ B）。

通俗理解：“如果能解决 B，就能用 B 的解法解决 A”，且转化过程很快（多项式时间）。

2. NP 完全问题（NPC）

满足两个条件：

问题本身属于NP（解能多项式时间验证）；
所有NP 问题都能多项式时间归约到它（即它是 NP 中 “最难” 的问题）。

问题关系类图

用类图展示 P、NP、NPC 问题的关系：

@startuml
class Problem {- name: string+ isPolynomialVerifiable(): bool  // 是否属于NP+ solve(): bool  // 求解（多项式/指数时间）
}class PProblem extends Problem {+ solve(): bool  // 重写：多项式时间求解
}class NPProblem extends Problem {+ verify(solution): bool  // 多项式时间验证解
}class NPCProblem extends NPProblem {+ reduceFrom(other: NPProblem): bool  // 其他NP问题可归约到它
}class Reduction {- from: NPProblem- to: NPCProblem+ apply(instance): any  // 多项式时间转化实例
}// 关联：归约连接NP问题和NPC问题
Reduction "1" -- "1" NPProblem : from
Reduction "1" -- "1" NPCProblem : to// 实例化具体问题
PProblem "1" -- "1" "Dijkstra（最短路径）"
NPProblem "1" -- "1" "哈密顿回路"
NPCProblem "1" -- "1" "团问题"
NPCProblem "1" -- "1" "顶点覆盖问题"@enduml

34.4 NP 完全性的证明

证明四步法

要证明一个问题 L 是 NPC，只需遵循以下 4 步：

证明 L ∈ NP：设计一个多项式时间算法，验证 L 的任意候选解；
选择已知 NPC 问题 L'：比如团问题、SAT 问题（第一个被证明的 NPC 问题）；
证明 L' ≤ₚ L：构造多项式时间归约函数 f，将 L' 的实例转化为 L 的实例，且解等价；
结论：由于所有 NP 问题可归约到 L'，而 L' 可归约到 L，故所有 NP 问题可归约到 L，因此 L 是 NPC。

案例：证明顶点覆盖问题是 NPC

1. 顶点覆盖问题（VC）定义

给定无向图 G=(V,E) 和整数 k，是否存在一个顶点子集 S⊆V，使得 | S|≤k，且每一条边都至少有一个端点在 S 中（即 S “覆盖” 所有边）。

2. 证明步骤

步骤 1：证明 VC ∈ NP

候选解：顶点子集 S；
验证：检查 | S|≤k，且对每一条边 (u,v)，u∈S 或 v∈S（遍历所有边，O (E) 时间，多项式）。

步骤 2：选择已知 NPC 问题 L'—— 团问题

团问题（Clique）定义：给定图 G=(V,E) 和整数 k，是否存在子集 C⊆V，使得 | C|≥k，且 C 是完全子图（任意两顶点间有边）。

步骤 3：证明团问题 ≤ₚ 顶点覆盖问题

归约核心：图 G 的顶点覆盖 S，等价于其补图 G' 的团 C=V\S（补图 G' 中，u 和 v 有边当且仅当 G 中 u 和 v 无边）。

具体归约函数 f：

输入：团问题实例 (G, k)；
输出：顶点覆盖问题实例 (G', |V| - k)；
等价性：G 有大小≥k 的团 ⇨ G' 有大小≤|V| - k 的顶点覆盖。

步骤 4：结论

VC ∈ NP，且团问题（NPC）可归约到 VC，故 VC 是 NPC。

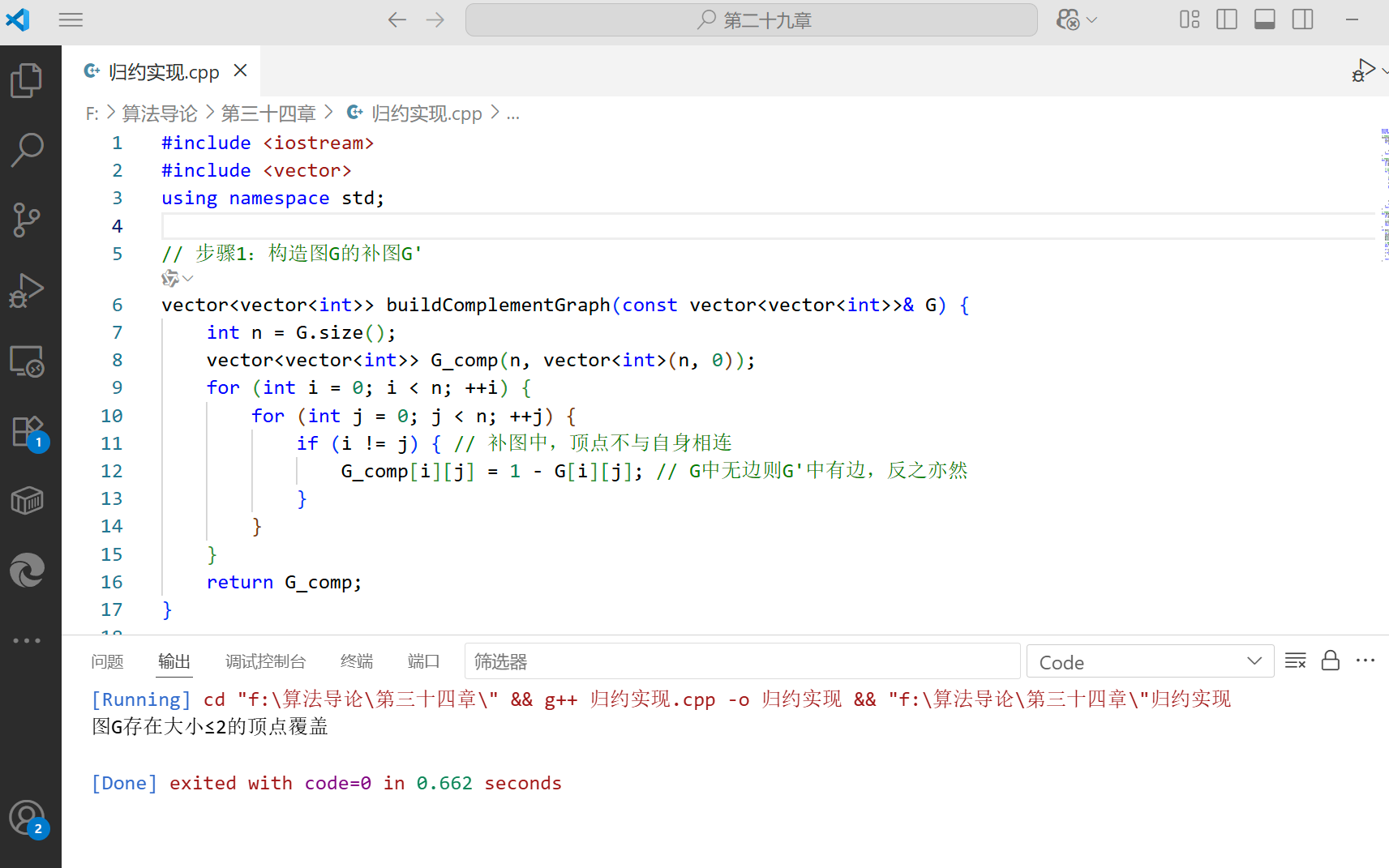
归约实现代码（C++）

#include <iostream>
#include <vector>
using namespace std;// 步骤1：构造图G的补图G'
vector<vector<int>> buildComplementGraph(const vector<vector<int>>& G) {int n = G.size();vector<vector<int>> G_comp(n, vector<int>(n, 0));for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i != j) { // 补图中，顶点不与自身相连G_comp[i][j] = 1 - G[i][j]; // G中无边则G'中有边，反之亦然}}}return G_comp;
}// 步骤2：暴力检查图是否有大小≥k的团（已知团是NPC，此处用暴力演示）
bool hasClique(const vector<vector<int>>& G, int k) {int n = G.size();if (k == 0) return true;if (k > n) return false;// 用位运算枚举所有大小为k的顶点子集（n≤20时可行）// mask的二进制表示中，1的位置表示选中的顶点for (int mask = 1; mask < (1 << n); ++mask) {if (__builtin_popcount(mask) != k) continue; // 只保留大小为k的子集// 检查子集中所有顶点是否两两有边（是否为团）vector<int> clique;for (int i = 0; i < n; ++i) {if (mask & (1 << i)) clique.push_back(i);}bool isClique = true;for (int i = 0; i < k; ++i) {for (int j = i + 1; j < k; ++j) {if (G[clique[i]][clique[j]] != 1) {isClique = false;break;}}if (!isClique) break;}if (isClique) return true;}return false;
}// 步骤3：归约验证顶点覆盖（通过补图的团）
bool hasVertexCover(const vector<vector<int>>& G, int k) {int n = G.size();if (k < 0 || k > n) return false;// 归约：G有大小≤k的顶点覆盖 ⇨ G'有大小≥n-k的团vector<vector<int>> G_comp = buildComplementGraph(G);int requiredCliqueSize = n - k;return hasClique(G_comp, requiredCliqueSize);
}int main() {// 测试案例：图G（4个顶点，边0-1,1-2,2-3）int n = 4;vector<vector<int>> G(n, vector<int>(n, 0));G[0][1] = G[1][0] = 1;G[1][2] = G[2][1] = 1;G[2][3] = G[3][2] = 1;// 问题：G是否有大小≤2的顶点覆盖？（答案：是，如{1,2}）int k = 2;bool result = hasVertexCover(G, k);if (result) {cout << "图G存在大小≤" << k << "的顶点覆盖" << endl;} else {cout << "图G不存在大小≤" << k << "的顶点覆盖" << endl;}return 0;
}

34.5 NP 完全问题（含完整代码）

本节针对 5 个经典 NPC 问题，分别讲解定义、实例和可运行代码（注：NPC 问题无多项式解法，代码用暴力或动态规划优化，仅适用于小规模实例）。

34.5.1 团问题（Clique）

问题定义

给定无向图 G=(V,E)，找到最大的顶点子集 C⊆V，使得 C 是完全子图（任意两顶点间有边），这个子集 C 称为最大团。

完整代码（暴力搜索最大团）

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;// 检查一个顶点子集是否为团（任意两顶点间有边）
bool isClique(const vector<vector<int>>& graph, const vector<int>& subset) {int m = subset.size();for (int i = 0; i < m; ++i) {for (int j = i + 1; j < m; ++j) {if (graph[subset[i]][subset[j]] != 1) {return false;}}}return true;
}// 暴力搜索最大团（枚举所有可能的顶点子集）
vector<int> findMaxClique(const vector<vector<int>>& graph) {int n = graph.size();vector<int> maxClique;// 用位运算枚举所有子集（mask从1到2^n-1）for (int mask = 1; mask < (1 << n); ++mask) {vector<int> currentSubset;for (int i = 0; i < n; ++i) {if (mask & (1 << i)) {currentSubset.push_back(i);}}// 若当前子集是团，且比之前的最大团大，则更新if (isClique(graph, currentSubset) && currentSubset.size() > maxClique.size()) {maxClique = currentSubset;}}return maxClique;
}int main() {// 测试案例：图G（5个顶点，边0-1,0-2,1-2,1-3,2-3,3-4）int n = 5;vector<vector<int>> graph(n, vector<int>(n, 0));graph[0][1] = graph[1][0] = 1;graph[0][2] = graph[2][0] = 1;graph[1][2] = graph[2][1] = 1;graph[1][3] = graph[3][1] = 1;graph[2][3] = graph[3][2] = 1;graph[3][4] = graph[4][3] = 1;vector<int> maxClique = findMaxClique(graph);// 输出结果cout << "最大团的大小：" << maxClique.size() << endl;cout << "最大团的顶点（编号0~n-1）：";for (int v : maxClique) {cout << v << " ";}cout << endl;return 0;
}

代码说明

枚举方式：用位运算mask表示子集（如mask=0b101表示选中顶点 0 和 2）；
时间复杂度：O (2ⁿ × n²)（n 是顶点数），仅适用于 n≤20 的小规模图；
测试案例输出：最大团大小为 3（顶点 1,2,3）。

34.5.2 顶点覆盖问题（Vertex Cover）

问题定义

给定无向图 G=(V,E)，找到最小的顶点子集 S⊆V，使得所有边都至少有一个端点在 S 中（即 S 覆盖所有边）。

完整代码（基于团归约的最小顶点覆盖）

#include <iostream>
#include <vector>
#include <climits>
using namespace std;// 构造补图（同34.4节）
vector<vector<int>> buildComplementGraph(const vector<vector<int>>& G) {int n = G.size();vector<vector<int>> G_comp(n, vector<int>(n, 0));for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i != j) G_comp[i][j] = 1 - G[i][j];}}return G_comp;
}// 检查图是否有大小≥k的团（同34.4节）
bool hasClique(const vector<vector<int>>& G, int k) {int n = G.size();if (k == 0) return true;if (k > n) return false;for (int mask = 1; mask < (1 << n); ++mask) {if (__builtin_popcount(mask) != k) continue;vector<int> clique;for (int i = 0; i < n; ++i) {if (mask & (1 << i)) clique.push_back(i);}bool isClique = true;for (int i = 0; i < k; ++i) {for (int j = i + 1; j < k; ++j) {if (G[clique[i]][clique[j]] != 1) {isClique = false;break;}}if (!isClique) break;}if (isClique) return true;}return false;
}// 找到最小顶点覆盖（从k=0开始尝试，直到找到最小k）
int findMinVertexCover(const vector<vector<int>>& G) {int n = G.size();vector<vector<int>> G_comp = buildComplementGraph(G);// 从最小可能的k开始尝试（k=0到k=n）for (int k = 0; k <= n; ++k) {int requiredCliqueSize = n - k;if (hasClique(G_comp, requiredCliqueSize)) {return k; // 找到最小k}}return n; // 最坏情况：所有顶点都是覆盖
}int main() {// 测试案例：同34.4节的图G（边0-1,1-2,2-3）int n = 4;vector<vector<int>> G(n, vector<int>(n, 0));G[0][1] = G[1][0] = 1;G[1][2] = G[2][1] = 1;G[2][3] = G[3][2] = 1;int minSize = findMinVertexCover(G);cout << "最小顶点覆盖的大小：" << minSize << endl;return 0;
}

34.5.3 哈密顿回路问题（Hamiltonian Circuit）

问题定义

给定无向图 G=(V,E)，是否存在一条经过所有顶点恰好一次，最后回到起点的回路。

完整代码（暴力搜索哈密顿回路）

#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>  // 添加这个头文件以使用iota函数
using namespace std;// 检查一个顶点排列是否构成哈密顿回路
bool isHamiltonianCircuit(const vector<vector<int>>& graph, const vector<int>& path) {int n = graph.size();if (path.size() != n) return false;// 检查所有顶点是否唯一vector<bool> visited(n, false);for (int v : path) {if (visited[v]) return false;visited[v] = true;}// 检查相邻顶点（含最后一个与第一个）是否有边for (int i = 0; i < n; ++i) {int u = path[i];int v = path[(i + 1) % n];if (graph[u][v] != 1) return false;}return true;
}// 暴力搜索哈密顿回路（枚举所有顶点排列）
vector<int> findHamiltonianCircuit(const vector<vector<int>>& graph) {int n = graph.size();vector<int> path(n);// 初始化路径为0,1,2,...,n-1iota(path.begin(), path.end(), 0);// 枚举所有排列（next_permutation生成所有顺序）do {if (isHamiltonianCircuit(graph, path)) {return path; // 找到回路，返回}} while (next_permutation(path.begin() + 1, path.end())); // 固定起点为0（避免重复枚举旋转后的回路，如0-1-2和1-2-0是同一回路）return {}; // 无哈密顿回路
}int main() {// 测试案例1：有哈密顿回路的图（0-1-2-3-0）int n1 = 4;vector<vector<int>> graph1(n1, vector<int>(n1, 0));graph1[0][1] = graph1[1][0] = 1;graph1[1][2] = graph1[2][1] = 1;graph1[2][3] = graph1[3][2] = 1;graph1[3][0] = graph1[0][3] = 1;vector<int> circuit1 = findHamiltonianCircuit(graph1);if (!circuit1.empty()) {cout << "图1的哈密顿回路：";for (int v : circuit1) cout << v << " ";cout << circuit1[0] << "（回到起点）" << endl;} else {cout << "图1无哈密顿回路" << endl;}// 测试案例2：无哈密顿回路的图（0-1,1-2,2-0,0-3）int n2 = 4;vector<vector<int>> graph2(n2, vector<int>(n2, 0));graph2[0][1] = graph2[1][0] = 1;graph2[1][2] = graph2[2][1] = 1;graph2[2][0] = graph2[0][2] = 1;graph2[0][3] = graph2[3][0] = 1;vector<int> circuit2 = findHamiltonianCircuit(graph2);if (!circuit2.empty()) {cout << "图2的哈密顿回路：";for (int v : circuit2) cout << v << " ";cout << circuit2[0] << endl;} else {cout << "图2无哈密顿回路" << endl;}return 0;
}

34.5.4 旅行商问题（TSP）

问题定义

给定 n 个城市和两两之间的距离，找到一条经过所有城市恰好一次，最后回到起点的最短回路。

完整代码（动态规划优化 TSP）

TSP 的暴力解法是 O (n!)，动态规划可优化到 O (n²2ⁿ)，适用于 n≤20 的实例。

#include <iostream>
#include <vector>
#include <climits>
using namespace std;const int INF = INT_MAX / 2; // 避免溢出// 动态规划求解TSP（返回最短回路长度）
int tspDP(const vector<vector<int>>& dist) {int n = dist.size();// dp[mask][u]：访问过mask中的城市，最后停在u的最短距离vector<vector<int>> dp(1 << n, vector<int>(n, INF));// 初始化：只访问单个城市u，距离为0（起点可任选，此处选0）dp[1 << 0][0] = 0;// 枚举所有状态（mask表示已访问的城市）for (int mask = 1; mask < (1 << n); ++mask) {// 枚举当前所在的城市ufor (int u = 0; u < n; ++u) {if (!(mask & (1 << u))) continue; // u未被访问，跳过if (dp[mask][u] == INF) continue; // 此状态不可达，跳过// 尝试访问未访问的城市vfor (int v = 0; v < n; ++v) {if (mask & (1 << v)) continue; // v已被访问，跳过// 新状态：mask | (1<<v)（加入v），最后停在vint newMask = mask | (1 << v);dp[newMask][v] = min(dp[newMask][v], dp[mask][u] + dist[u][v]);}}}// 最后一步：从任意城市u回到起点0，形成回路int fullMask = (1 << n) - 1; // 所有城市都已访问int minDist = INF;for (int u = 1; u < n; ++u) {minDist = min(minDist, dp[fullMask][u] + dist[u][0]);}return minDist;
}int main() {// 测试案例：4个城市的距离矩阵（dist[i][j]是城市i到j的距离）vector<vector<int>> dist = {{0, 10, 15, 20},{10, 0, 35, 25},{15, 35, 0, 30},{20, 25, 30, 0}};int minCircuit = tspDP(dist);cout << "TSP最短回路长度：" << minCircuit << endl;return 0;
}

代码说明

状态定义：dp[mask][u]表示 “访问过mask对应的城市，最后在城市u” 的最短距离；
初始化：仅访问起点 0 时，距离为 0；
状态转移：从u到未访问的v，更新新状态的距离；
最终结果：所有城市访问完后，从任意u回到 0 的最短距离。

34.5.5 子集和问题（Subset Sum）

问题定义

给定整数集合 S 和目标和 T，是否存在一个子集 S'⊆S，使得 S' 中所有元素的和等于 T。

完整代码（动态规划求解子集和）

动态规划时间复杂度 O (nT)（n 是集合大小，T 是目标和），空间可优化到 O (T)。

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;// 动态规划求解子集和问题（返回是否存在满足条件的子集）
bool subsetSumDP(const vector<int>& nums, int target) {int n = nums.size();// dp[i]：是否存在子集和等于ivector<bool> dp(target + 1, false);dp[0] = true; // 空子集和为0，初始为true// 遍历每个数字，更新dp数组for (int num : nums) {// 逆序遍历：避免重复使用同一个数字（0-1背包问题思路）for (int i = target; i >= num; --i) {if (dp[i - num]) {dp[i] = true;}}}return dp[target];
}// 扩展：找到一个满足条件的子集（可选）
vector<int> findSubset(const vector<int>& nums, int target) {int n = nums.size();vector<bool> dp(target + 1, false);vector<vector<bool>> chosen(n, vector<bool>(target + 1, false)); // 记录是否选择第i个数字dp[0] = true;for (int i = 0; i < n; ++i) {int num = nums[i];for (int j = target; j >= num; --j) {if (dp[j - num] && !dp[j]) {dp[j] = true;chosen[i][j] = true; // 选择第i个数字来组成和j}}}// 回溯找到子集vector<int> subset;int currentSum = target;for (int i = n - 1; i >= 0; --i) {if (chosen[i][currentSum]) {subset.push_back(nums[i]);currentSum -= nums[i];}}reverse(subset.begin(), subset.end()); // 调整顺序return subset;
}int main() {// 测试案例1：存在子集和（集合{3,34,4,12,5,2}，目标和9）vector<int> nums1 = {3, 34, 4, 12, 5, 2};int target1 = 9;bool hasSolution1 = subsetSumDP(nums1, target1);if (hasSolution1) {vector<int> subset1 = findSubset(nums1, target1);cout << "案例1：存在子集和等于" << target1 << "，子集为：";for (int num : subset1) cout << num << " ";cout << endl;} else {cout << "案例1：不存在子集和等于" << target1 << endl;}// 测试案例2：不存在子集和（集合{1,2,5}，目标和4）vector<int> nums2 = {1, 2, 5};int target2 = 4;bool hasSolution2 = subsetSumDP(nums2, target2);if (hasSolution2) {vector<int> subset2 = findSubset(nums2, target2);cout << "案例2：存在子集和等于" << target2 << "，子集为：";for (int num : subset2) cout << num << " ";cout << endl;} else {cout << "案例2：不存在子集和等于" << target2 << endl;}return 0;
}

思考题

证明独立集问题是 NPC：独立集问题定义为 “给定图 G 和 k，是否存在子集 S⊆V，使得 | S|≥k 且 S 中任意两顶点无边”。提示：归约自团问题（独立集与团在补图中等价）。
优化子集和的空间：当前动态规划代码空间是 O (T)，能否进一步优化到 O (1)？提示：利用位运算（用一个整数的二进制位表示 dp 状态）。
TSP 的实际应用：既然 TSP 是 NPC，为什么实际中还能解决？提示：近似算法（如贪心、模拟退火）、问题规模限制（如物流中城市数≤100）。

本章注记

历史背景：NP 完全性理论由 Cook 在 1971 年提出，他证明了布尔可满足性问题（SAT） 是第一个 NPC 问题；1972 年 Karp 证明了团、顶点覆盖等 21 个经典问题是 NPC，奠定了 NP 完全性的基础。
实际意义：遇到 NPC 问题时，无需执着于 “多项式解法”，而是选择：
- 小规模实例：用暴力或动态规划；
- 大规模实例：用近似算法、启发式算法（如遗传算法、模拟退火）；
- 限制问题条件：如 “欧几里得 TSP”（距离满足三角不等式）有近似比 1.5 的算法。
开放问题：P=NP？这是千禧年七大数学难题之一，若证明 P=NP，将彻底改变密码学、人工智能等领域（如 RSA 加密将失效，NP 问题可高效解决）。